Menu Close

1-x-1-3-x-x-1-4-2-x-x-2-2x-2-2-

Tinku Tara 0 Comments
Pin




Question Number 164809 by mathlove last updated on 22/Jan/22
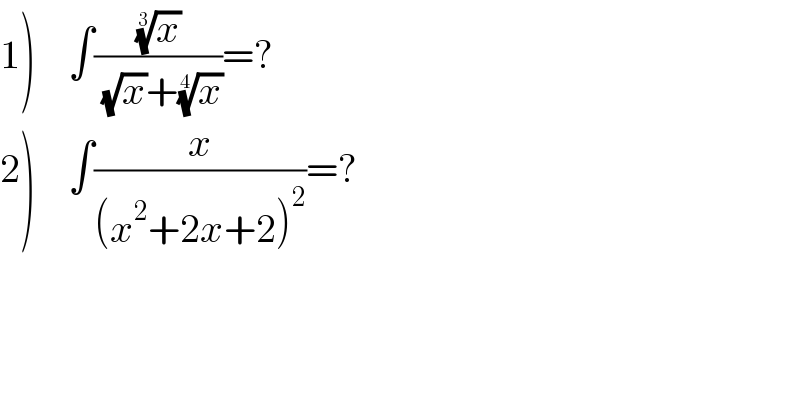
1) ∫((x)^(1/3) /( (√x)+(x)^(1/4) ))=? 2) ∫(x/((x^2 +2x+2)^2 ))=?
$$\left.\mathrm{1}\right)\:\:\:\:\int\frac{\sqrt[{\mathrm{3}}]{{x}}}{\:\sqrt{{x}}+\sqrt[{\mathrm{4}}]{{x}}}=? \\ $$$$\left.\mathrm{2}\right)\:\:\:\:\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }=? \\ $$
Answered by Ar Brandon last updated on 22/Jan/22
Ostrogradsky ∫(x/((x^2 +2x+2)^2 ))dx=((px+q)/(x^2 +2x+2))+∫((rx+s)/(x^2 +2x+2))dx ⇒(x/((x^2 +2x+2)^2 ))=((p(x^2 +2x+2)−(px+q)(2x+2))/((x^2 +2x+2)^2 ))+((rx+s)/(x^2 +2x+2)) { ((r=^x^3 0)),((p−2p+2r+s=^x^2 0)),((2p−2p−2q+2r+2s=^x 1)),((2p−2q+2s=^x^0 0)) :}⇒p=−(1/2), q=−1, s=−(1/2) ⇒∫(x/((x^2 +2x+2)^2 ))dx=−((x+2)/(2(x^2 +2x+2)))−(1/2)∫(dx/(x^2 +2x+2)) ⇒∫(x/((x^2 +2x+2)^2 ))dx=−((x+2)/(2(x^2 +2x+2)))−(1/2)tan^(−1) (x+1)+C
$$\mathrm{Ostrogradsky} \\ $$$$\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx}=\frac{{px}+{q}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}+\int\frac{{rx}+{s}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}{dx} \\ $$$$\Rightarrow\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }=\frac{{p}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)−\left({px}+{q}\right)\left(\mathrm{2}{x}+\mathrm{2}\right)}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{{rx}+{s}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}} \\ $$$$\begin{cases}{{r}\overset{{x}^{\mathrm{3}} } {=}\mathrm{0}}\\{{p}−\mathrm{2}{p}+\mathrm{2}{r}+{s}\overset{{x}^{\mathrm{2}} } {=}\mathrm{0}}\\{\mathrm{2}{p}−\mathrm{2}{p}−\mathrm{2}{q}+\mathrm{2}{r}+\mathrm{2}{s}\overset{{x}} {=}\mathrm{1}}\\{\mathrm{2}{p}−\mathrm{2}{q}+\mathrm{2}{s}\overset{{x}^{\mathrm{0}} } {=}\mathrm{0}}\end{cases}\Rightarrow{p}=−\frac{\mathrm{1}}{\mathrm{2}},\:{q}=−\mathrm{1},\:{s}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx}=−\frac{{x}+\mathrm{2}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}} \\ $$$$\Rightarrow\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx}=−\frac{{x}+\mathrm{2}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left({x}+\mathrm{1}\right)+{C} \\ $$
Answered by Ar Brandon last updated on 22/Jan/22
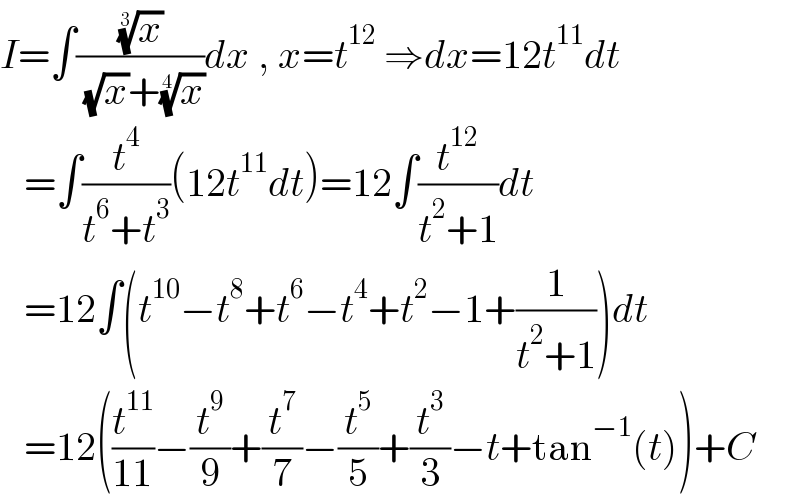
I=∫((x)^(1/3) /( (√x)+(x)^(1/4) ))dx , x=t^(12) ⇒dx=12t^(11) dt =∫(t^4 /(t^6 +t^3 ))(12t^(11) dt)=12∫(t^(12) /(t^2 +1))dt =12∫(t^(10) −t^8 +t^6 −t^4 +t^2 −1+(1/(t^2 +1)))dt =12((t^(11) /(11))−(t^9 /9)+(t^7 /7)−(t^5 /5)+(t^3 /3)−t+tan^(−1) (t))+C
$${I}=\int\frac{\sqrt[{\mathrm{3}}]{{x}}}{\:\sqrt{{x}}+\sqrt[{\mathrm{4}}]{{x}}}{dx}\:,\:{x}={t}^{\mathrm{12}} \:\Rightarrow{dx}=\mathrm{12}{t}^{\mathrm{11}} {dt} \\ $$$$\:\:\:=\int\frac{{t}^{\mathrm{4}} }{{t}^{\mathrm{6}} +{t}^{\mathrm{3}} }\left(\mathrm{12}{t}^{\mathrm{11}} {dt}\right)=\mathrm{12}\int\frac{{t}^{\mathrm{12}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$\:\:\:=\mathrm{12}\int\left({t}^{\mathrm{10}} −{t}^{\mathrm{8}} +{t}^{\mathrm{6}} −{t}^{\mathrm{4}} +{t}^{\mathrm{2}} −\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt} \\ $$$$\:\:\:=\mathrm{12}\left(\frac{{t}^{\mathrm{11}} }{\mathrm{11}}−\frac{{t}^{\mathrm{9}} }{\mathrm{9}}+\frac{{t}^{\mathrm{7}} }{\mathrm{7}}−\frac{{t}^{\mathrm{5}} }{\mathrm{5}}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−{t}+\mathrm{tan}^{−\mathrm{1}} \left({t}\right)\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *