Question Number 62907 by aliesam last updated on 26/Jun/19
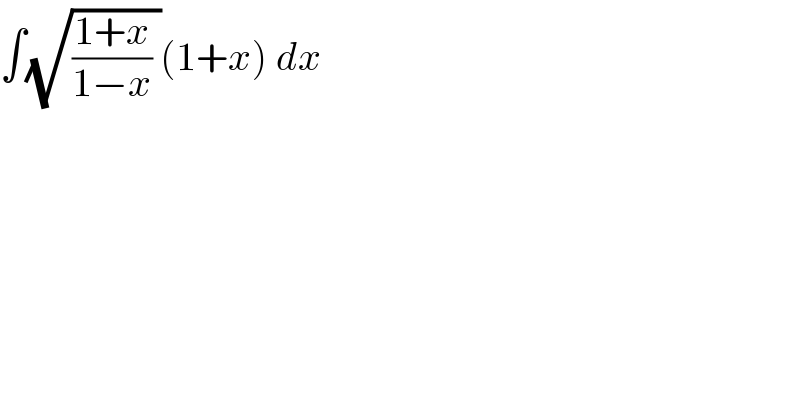
$$\int\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\:}\left(\mathrm{1}+{x}\right)\:{dx} \\ $$
Commented by mathmax by abdo last updated on 26/Jun/19
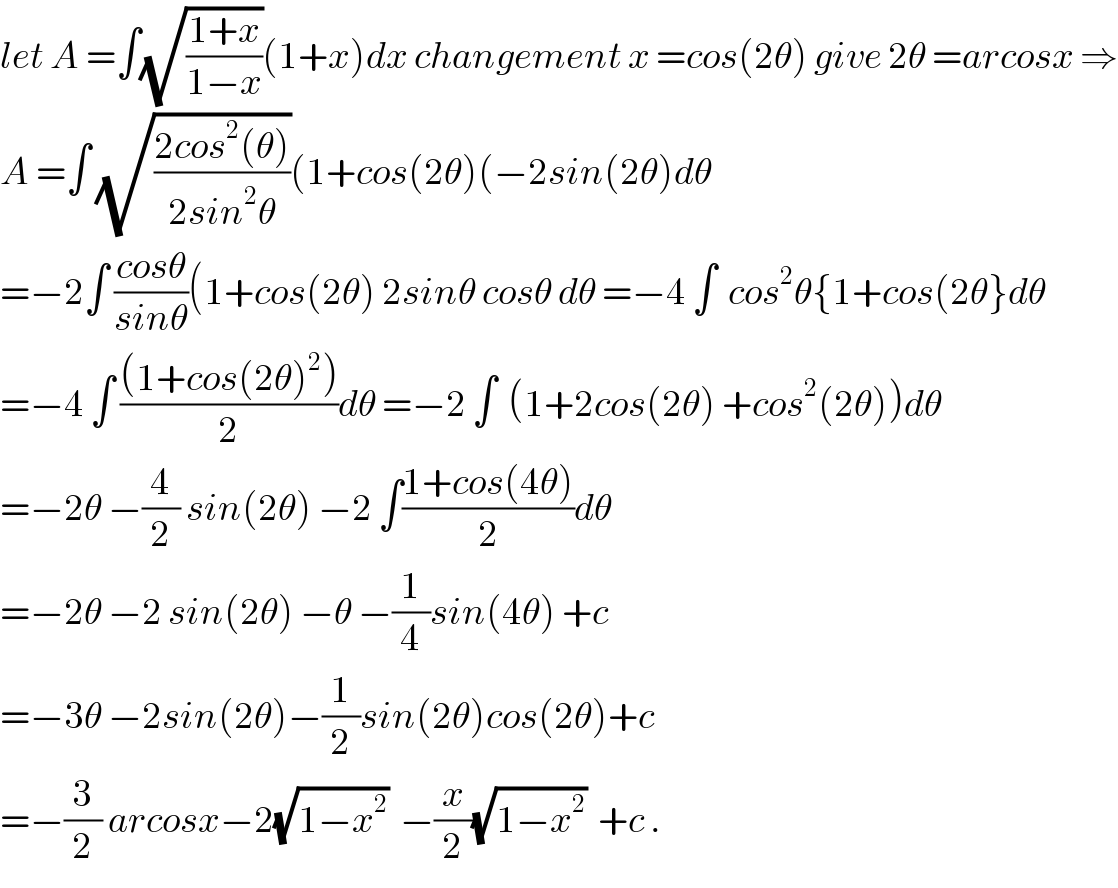
$${let}\:{A}\:=\int\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\left(\mathrm{1}+{x}\right){dx}\:{changement}\:{x}\:={cos}\left(\mathrm{2}\theta\right)\:{give}\:\mathrm{2}\theta\:={arcosx}\:\Rightarrow \\ $$$${A}\:=\int\:\sqrt{\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\theta\right)}{\mathrm{2}{sin}^{\mathrm{2}} \theta}}\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\left(−\mathrm{2}{sin}\left(\mathrm{2}\theta\right){d}\theta\right.\right. \\ $$$$=−\mathrm{2}\int\:\frac{{cos}\theta}{{sin}\theta}\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\:\mathrm{2}{sin}\theta\:{cos}\theta\:{d}\theta\:=−\mathrm{4}\:\int\:\:{cos}^{\mathrm{2}} \theta\left\{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right\}{d}\theta\right.\right. \\ $$$$=−\mathrm{4}\:\int\:\frac{\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)^{\mathrm{2}} \right)}{\mathrm{2}}{d}\theta\:=−\mathrm{2}\:\int\:\:\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=−\mathrm{2}\theta\:−\frac{\mathrm{4}}{\mathrm{2}}\:{sin}\left(\mathrm{2}\theta\right)\:−\mathrm{2}\:\int\frac{\mathrm{1}+{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}{d}\theta \\ $$$$=−\mathrm{2}\theta\:−\mathrm{2}\:{sin}\left(\mathrm{2}\theta\right)\:−\theta\:−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{4}\theta\right)\:+{c} \\ $$$$=−\mathrm{3}\theta\:−\mathrm{2}{sin}\left(\mathrm{2}\theta\right)−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right){cos}\left(\mathrm{2}\theta\right)+{c} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\:{arcosx}−\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\:−\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\:+{c}\:. \\ $$
Answered by Hope last updated on 26/Jun/19

$$\int\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\int\frac{\mathrm{2}{xdx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${x}={sina}\:\:{dx}={cosada} \\ $$$$\int\frac{{cosada}}{{cosa}}+\int\frac{\mathrm{2}{sina}×{cosada}}{{cosa}}+\int\frac{{sin}^{\mathrm{2}} {a}×{cosada}}{{cosa}} \\ $$$$\int{da}+\mathrm{2}\int{sinada}+\int\frac{\mathrm{1}−{cos}\mathrm{2}{a}}{\mathrm{2}}{da} \\ $$$$\int{da}+\mathrm{2}\int{sinada}+\frac{\mathrm{1}}{\mathrm{2}}\int{da}−\frac{\mathrm{1}}{\mathrm{2}}\int{cos}\mathrm{2}{ada} \\ $$$${a}−\mathrm{2}{cosa}+\frac{\mathrm{1}}{\mathrm{2}}{a}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{{sin}\mathrm{2}{a}}{\mathrm{2}}+{c} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left({x}\right)−\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{2}{x}×\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+{c} \\ $$
Commented by mathmax by abdo last updated on 26/Jun/19
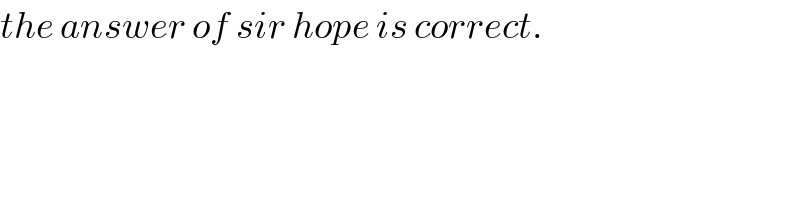
$${the}\:{answer}\:{of}\:{sir}\:{hope}\:{is}\:{correct}. \\ $$
Commented by aliesam last updated on 26/Jun/19
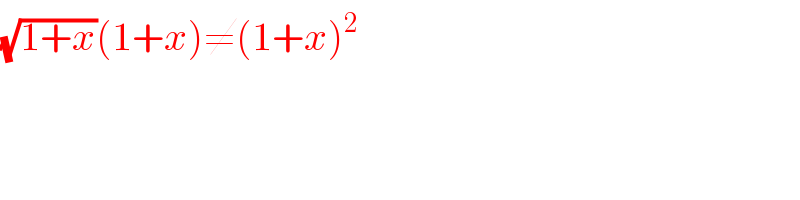
$$\sqrt{\mathrm{1}+{x}}\left(\mathrm{1}+{x}\right)\neq\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \\ $$
Commented by peter frank last updated on 26/Jun/19
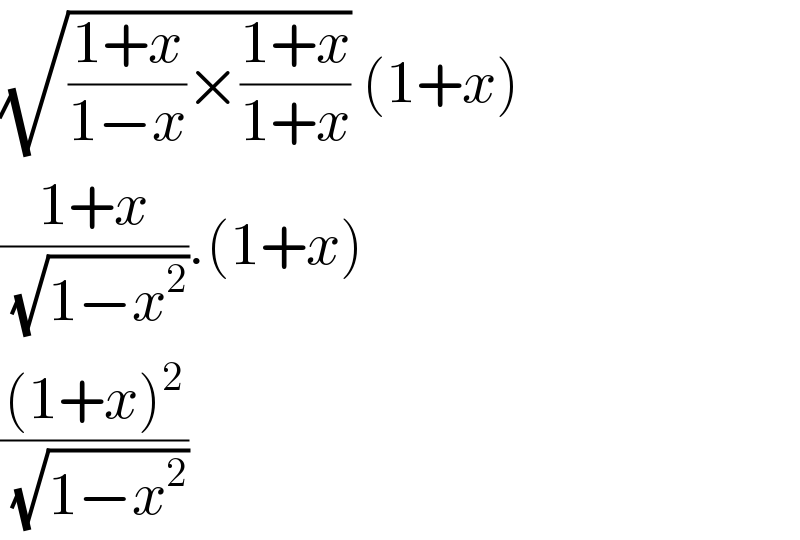
$$\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}×\frac{\mathrm{1}+{x}}{\mathrm{1}+{x}}}\:\left(\mathrm{1}+{x}\right) \\ $$$$\frac{\mathrm{1}+{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}.\left(\mathrm{1}+{x}\right) \\ $$$$\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$
Commented by aliesam last updated on 27/Jun/19
$${oh}\:{thats}\:{right}\:{so}\:{sorry}\:{sir} \\ $$
