Menu Close

1-x-1-x-2-dx-x-sin-w-cos-w-dw-sin-w-cos-w-dw-tan-w-1-sec-2-w-dw-tan-w-1-sec-2-w-du-u-1-u-2-1-u-tan-w-du-2-u-1-u-du-

Tinku Tara 0 Comments
Pin




Question Number 92397 by john santu last updated on 06/May/20
∫ (1/(x−(√(1−x^2 )))) dx [ x = sin w ] ∫ ((cos w dw)/(sin w−cos w)) = ∫ (dw/(tan w−1)) = ∫ ((sec^2 w dw)/((tan w−1)sec^2 w)) = ∫ (du/((u−1)(u^2 +1))) ; [ u = tan w ] = ∫ (du/(2(u−1)))−∫ ((u du )/(2(u^2 +1))) = (1/2)ln ∣u−1∣ −(1/4)ln∣u^2 +1∣ −(1/2)tan^(−1) (u) +c = (1/2)ln∣tan w−1∣−(1/4)ln∣tan^2 w+1∣− (1/2) tan^(−1) (tan w) +c = (1/2)ln∣(x/( (√(1−x^2 ))))−1∣+(1/4)ln∣1−x^2 ∣− (1/2)sin^(−1) (x) + c
$$\int\:\frac{\mathrm{1}}{{x}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx}\: \\ $$$$\left[\:{x}\:=\:\mathrm{sin}\:{w}\:\right]\: \\ $$$$\int\:\frac{\mathrm{cos}\:\mathrm{w}\:\mathrm{dw}}{\mathrm{sin}\:\mathrm{w}−\mathrm{cos}\:\mathrm{w}}\:=\:\int\:\frac{\mathrm{dw}}{\mathrm{tan}\:\mathrm{w}−\mathrm{1}} \\ $$$$=\:\int\:\frac{\mathrm{sec}^{\mathrm{2}} \:\mathrm{w}\:\mathrm{dw}}{\left(\mathrm{tan}\:\mathrm{w}−\mathrm{1}\right)\mathrm{sec}^{\mathrm{2}} \:\mathrm{w}} \\ $$$$=\:\int\:\frac{\mathrm{du}}{\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)}\:;\:\left[\:\mathrm{u}\:=\:\mathrm{tan}\:\mathrm{w}\:\right]\: \\ $$$$=\:\int\:\frac{\mathrm{du}}{\mathrm{2}\left(\mathrm{u}−\mathrm{1}\right)}−\int\:\frac{\mathrm{u}\:\mathrm{du}\:}{\mathrm{2}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{u}−\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{u}^{\mathrm{2}} +\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\:+\mathrm{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}\:\mathrm{w}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{tan}\:^{\mathrm{2}} \mathrm{w}+\mathrm{1}\mid− \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\mathrm{w}\right)\:+\mathrm{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{1}−{x}^{\mathrm{2}} \mid− \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\:+\:{c} \\ $$
Commented by abdomathmax last updated on 07/May/20
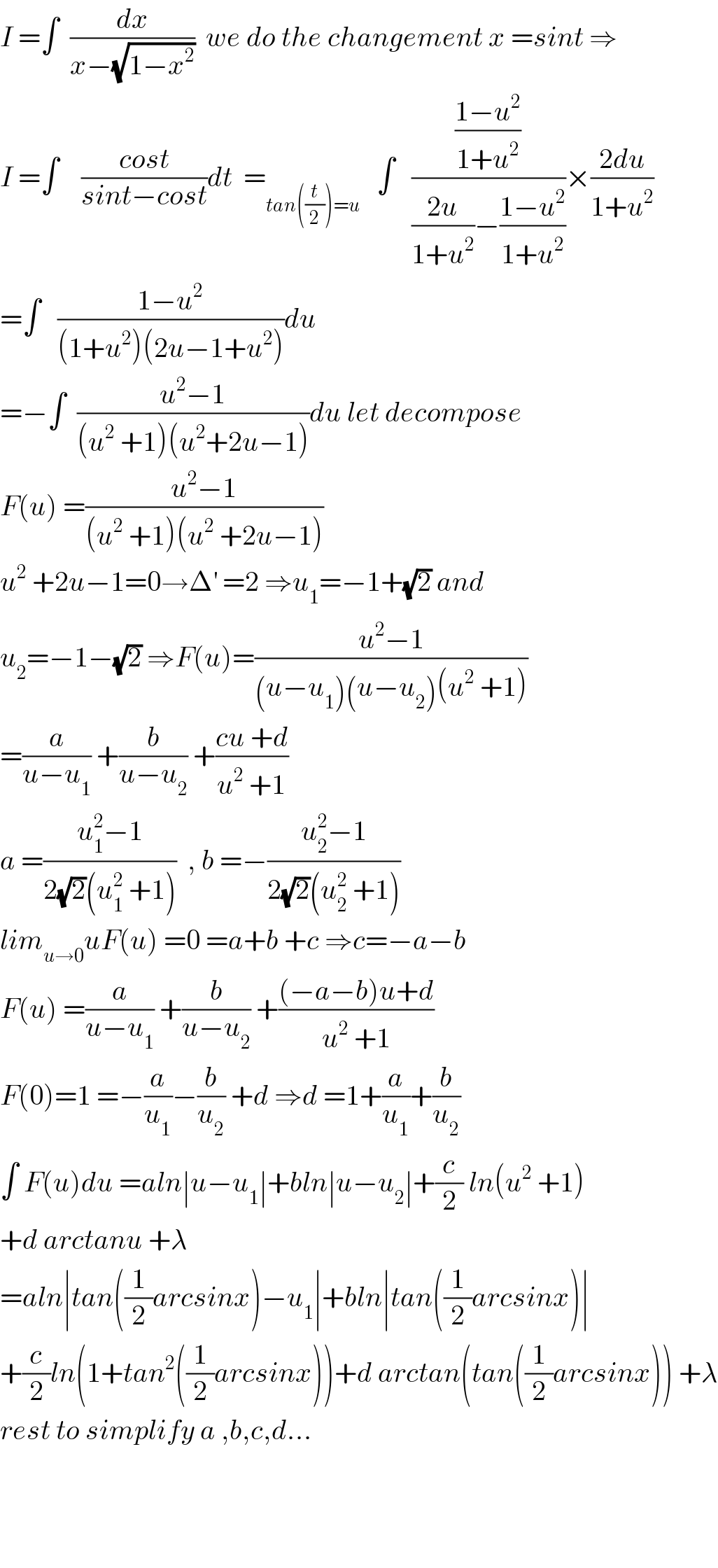
I =∫ (dx/(x−(√(1−x^2 )))) we do the changement x =sint ⇒ I =∫ ((cost)/(sint−cost))dt =_(tan((t/2))=u) ∫ (((1−u^2 )/(1+u^2 ))/(((2u)/(1+u^2 ))−((1−u^2 )/(1+u^2 ))))×((2du)/(1+u^2 )) =∫ ((1−u^2 )/((1+u^2 )(2u−1+u^2 )))du =−∫ ((u^2 −1)/((u^2 +1)(u^2 +2u−1)))du let decompose F(u) =((u^2 −1)/((u^2 +1)(u^2 +2u−1))) u^2 +2u−1=0→Δ^′ =2 ⇒u_1 =−1+(√2) and u_2 =−1−(√2) ⇒F(u)=((u^2 −1)/((u−u_1 )(u−u_2 )(u^2 +1))) =(a/(u−u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) a =((u_1 ^2 −1)/(2(√2)(u_1 ^2 +1))) , b =−((u_2 ^2 −1)/(2(√2)(u_2 ^2 +1))) lim_(u→0) uF(u) =0 =a+b +c ⇒c=−a−b F(u) =(a/(u−u_1 )) +(b/(u−u_2 )) +(((−a−b)u+d)/(u^2 +1)) F(0)=1 =−(a/u_1 )−(b/u_2 ) +d ⇒d =1+(a/u_1 )+(b/u_2 ) ∫ F(u)du =aln∣u−u_1 ∣+bln∣u−u_2 ∣+(c/2) ln(u^2 +1) +d arctanu +λ =aln∣tan((1/2)arcsinx)−u_1 ∣+bln∣tan((1/2)arcsinx)∣ +(c/2)ln(1+tan^2 ((1/2)arcsinx))+d arctan(tan((1/2)arcsinx)) +λ rest to simplify a ,b,c,d...
$${I}\:=\int\:\:\frac{{dx}}{{x}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:{we}\:{do}\:{the}\:{changement}\:{x}\:={sint}\:\Rightarrow \\ $$$${I}\:=\int\:\:\:\:\frac{{cost}}{{sint}−{cost}}{dt}\:\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\int\:\:\:\frac{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }−\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}×\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\int\:\:\:\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{2}{u}−\mathrm{1}+{u}^{\mathrm{2}} \right)}{du} \\ $$$$=−\int\:\:\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{1}\right)}{du}\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{2}{u}−\mathrm{1}\right)} \\ $$$${u}^{\mathrm{2}} \:+\mathrm{2}{u}−\mathrm{1}=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{2}\:\Rightarrow{u}_{\mathrm{1}} =−\mathrm{1}+\sqrt{\mathrm{2}}\:{and} \\ $$$${u}_{\mathrm{2}} =−\mathrm{1}−\sqrt{\mathrm{2}}\:\Rightarrow{F}\left({u}\right)=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:=\frac{{u}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\left({u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:,\:{b}\:=−\frac{{u}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\left({u}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${lim}_{{u}\rightarrow\mathrm{0}} {uF}\left({u}\right)\:=\mathrm{0}\:={a}+{b}\:+{c}\:\Rightarrow{c}=−{a}−{b} \\ $$$${F}\left({u}\right)\:=\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{\left(−{a}−{b}\right){u}+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{1}\:=−\frac{{a}}{{u}_{\mathrm{1}} }−\frac{{b}}{{u}_{\mathrm{2}} }\:+{d}\:\Rightarrow{d}\:=\mathrm{1}+\frac{{a}}{{u}_{\mathrm{1}} }+\frac{{b}}{{u}_{\mathrm{2}} } \\ $$$$\int\:{F}\left({u}\right){du}\:={aln}\mid{u}−{u}_{\mathrm{1}} \mid+{bln}\mid{u}−{u}_{\mathrm{2}} \mid+\frac{{c}}{\mathrm{2}}\:{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right) \\ $$$$+{d}\:{arctanu}\:+\lambda \\ $$$$={aln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsinx}\right)−{u}_{\mathrm{1}} \mid+{bln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsinx}\right)\mid \\ $$$$+\frac{{c}}{\mathrm{2}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{arcsinx}\right)\right)+{d}\:{arctan}\left({tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsinx}\right)\right)\:+\lambda \\ $$$${rest}\:{to}\:{simplify}\:{a}\:,{b},{c},{d}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by john santu last updated on 07/May/20
��������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *