Menu Close

1-x-1-x-5-1-3-dx-1-sin-2-x-5sin-x-6-dx-2z-5-4z-2-4z-5-dz-sec-5-5-tan-3-5-d-

Tinku Tara 0 Comments
Pin




Question Number 90321 by M±th+et£s last updated on 22/Apr/20
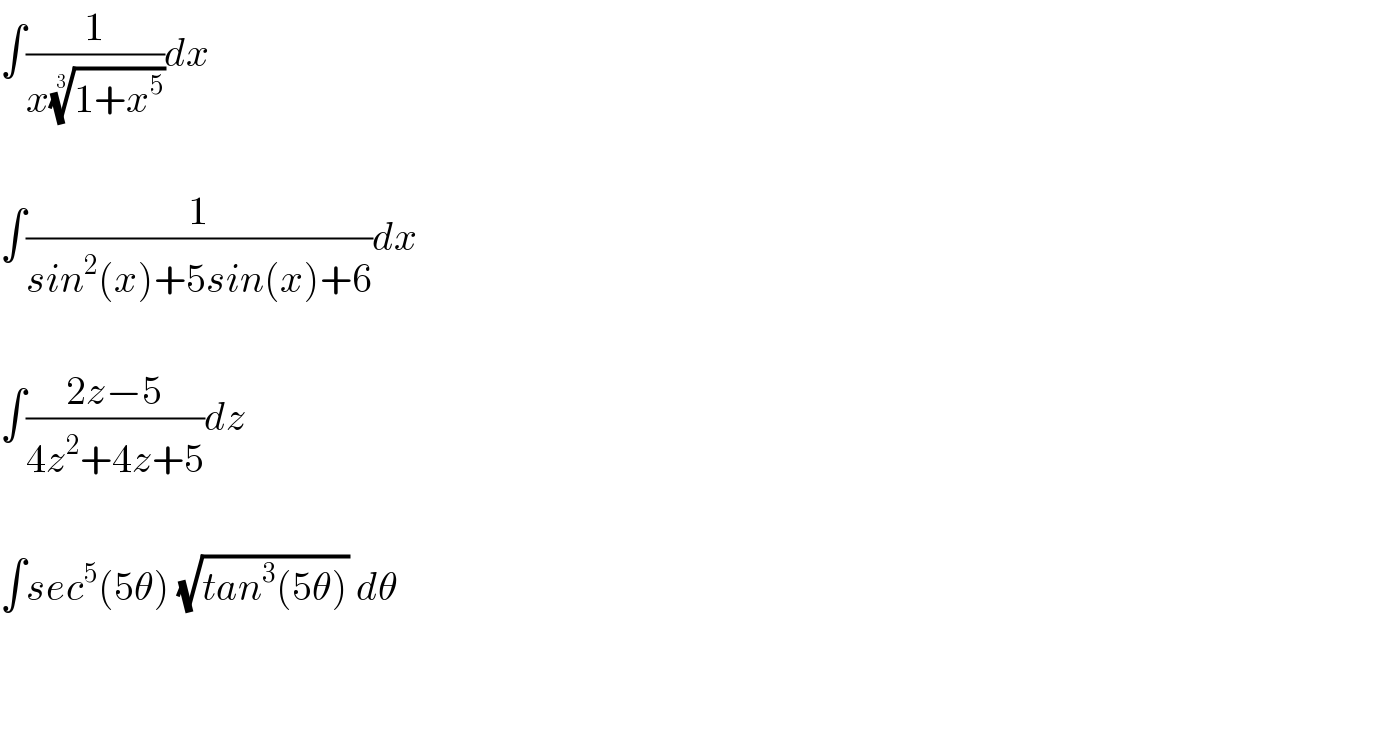
∫(1/(x((1+x^5 ))^(1/3) ))dx ∫(1/(sin^2 (x)+5sin(x)+6))dx ∫((2z−5)/(4z^2 +4z+5))dz ∫sec^5 (5θ) (√(tan^3 (5θ))) dθ
$$\int\frac{\mathrm{1}}{{x}\sqrt[{\mathrm{3}}]{\mathrm{1}+{x}^{\mathrm{5}} }}{dx} \\ $$$$ \\ $$$$\int\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left({x}\right)+\mathrm{5}{sin}\left({x}\right)+\mathrm{6}}{dx} \\ $$$$ \\ $$$$\int\frac{\mathrm{2}{z}−\mathrm{5}}{\mathrm{4}{z}^{\mathrm{2}} +\mathrm{4}{z}+\mathrm{5}}{dz} \\ $$$$ \\ $$$$\int{sec}^{\mathrm{5}} \left(\mathrm{5}\theta\right)\:\sqrt{{tan}^{\mathrm{3}} \left(\mathrm{5}\theta\right)}\:{d}\theta \\ $$$$ \\ $$$$ \\ $$
Commented by TANMAY PANACEA. last updated on 22/Apr/20
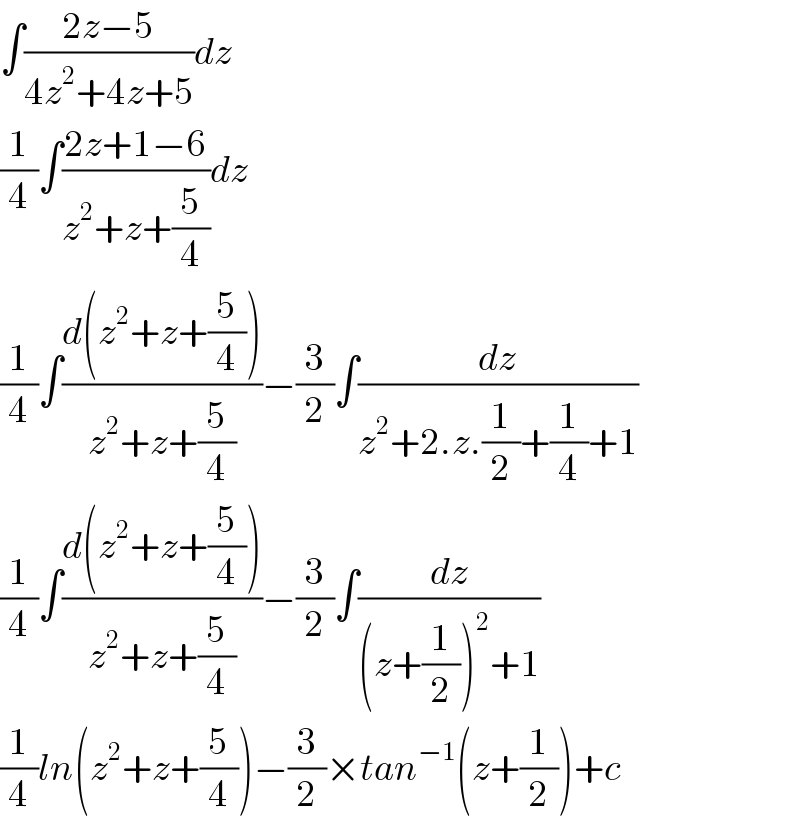
∫((2z−5)/(4z^2 +4z+5))dz (1/4)∫((2z+1−6)/(z^2 +z+(5/4)))dz (1/4)∫((d(z^2 +z+(5/4)))/(z^2 +z+(5/4)))−(3/2)∫(dz/(z^2 +2.z.(1/2)+(1/4)+1)) (1/4)∫((d(z^2 +z+(5/4)))/(z^2 +z+(5/4)))−(3/2)∫(dz/((z+(1/2))^2 +1)) (1/4)ln(z^2 +z+(5/4))−(3/2)×tan^(−1) (z+(1/2))+c
$$\int\frac{\mathrm{2}{z}−\mathrm{5}}{\mathrm{4}{z}^{\mathrm{2}} +\mathrm{4}{z}+\mathrm{5}}{dz} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{z}+\mathrm{1}−\mathrm{6}}{{z}^{\mathrm{2}} +{z}+\frac{\mathrm{5}}{\mathrm{4}}}{dz} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{d}\left({z}^{\mathrm{2}} +{z}+\frac{\mathrm{5}}{\mathrm{4}}\right)}{{z}^{\mathrm{2}} +{z}+\frac{\mathrm{5}}{\mathrm{4}}}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dz}}{{z}^{\mathrm{2}} +\mathrm{2}.{z}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{d}\left({z}^{\mathrm{2}} +{z}+\frac{\mathrm{5}}{\mathrm{4}}\right)}{{z}^{\mathrm{2}} +{z}+\frac{\mathrm{5}}{\mathrm{4}}}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dz}}{\left({z}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({z}^{\mathrm{2}} +{z}+\frac{\mathrm{5}}{\mathrm{4}}\right)−\frac{\mathrm{3}}{\mathrm{2}}×{tan}^{−\mathrm{1}} \left({z}+\frac{\mathrm{1}}{\mathrm{2}}\right)+{c} \\ $$
Commented by M±th+et£s last updated on 22/Apr/20
nice work sir
$${nice}\:{work}\:{sir} \\ $$
Answered by TANMAY PANACEA. last updated on 22/Apr/20
2)∫(dx/((sinx+3)(sinx+2))) ∫(dx/(sinx+2))−∫(dx/(sinx+3)) now easy I_1 =∫(dx/(2+((2tan(x/2))/(1+tan^2 (x/2))))) =∫((sec^2 (x/2))/(2+2tan^2 (x/2)+2tan(x/2)))dx k=tan(x/2)→dk=(1/2)sec^2 (x/2)dx ∫((2dk)/(2+2k^2 +2k))=∫(dk/(k^2 +2.k.(1/2)+(1/4)+(3/4)))=∫(dk/((k+(1/2))^2 +((((√3) )/2))^2 )) (2/( (√3)))tan^(−1) (((k+(1/2))/((√3)/2)))+c_1 =(2/( (√3)))tan^(−1) (((tan(x/2)+(1/2))/((√3)/2)))+c_1 similarly we can find ∫(dx/(3+sinx))
$$\left.\mathrm{2}\right)\int\frac{{dx}}{\left({sinx}+\mathrm{3}\right)\left({sinx}+\mathrm{2}\right)} \\ $$$$\int\frac{{dx}}{{sinx}+\mathrm{2}}−\int\frac{{dx}}{{sinx}+\mathrm{3}} \\ $$$${now}\:{easy} \\ $$$${I}_{\mathrm{1}} =\int\frac{{dx}}{\mathrm{2}+\frac{\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$=\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}+\mathrm{2}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}}{dx} \\ $$$${k}={tan}\frac{{x}}{\mathrm{2}}\rightarrow{dk}=\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx} \\ $$$$\int\frac{\mathrm{2}{dk}}{\mathrm{2}+\mathrm{2}{k}^{\mathrm{2}} +\mathrm{2}{k}}=\int\frac{{dk}}{{k}^{\mathrm{2}} +\mathrm{2}.{k}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}}=\int\frac{{dk}}{\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{k}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+{c}_{\mathrm{1}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+{c}_{\mathrm{1}} \\ $$$${similarly}\:{we}\:{can}\:{find} \\ $$$$\int\frac{{dx}}{\mathrm{3}+{sinx}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 22/Apr/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by peter frank last updated on 22/Apr/20
thank you
$${thank}\:{you} \\ $$
Answered by TANMAY PANACEA. last updated on 22/Apr/20
∫(dx/(x(1+x^5 )^(1/3) ))=∫(x^4 /(x^5 (1+x^5 )^(1/3) ))dx t=x^5 dt=5x^4 dx ∫(dt/(5×t×(1+t)^(1/3) )) (1/5)∫(dt/(t(1+t)^(1/3) )) k^3 =1+t (1/5)∫((3k^2 dk)/((k^3 −1)k)) (3/5)∫((kdk)/((k−1)(k^2 +k+1))) (k/((k−1)(k^2 +k+1)))=(a/(k−1))+((bk+c)/((k^2 +k+1))) k=ak^2 +ak+a+bk^2 +ck−bk−c k=k^2 (a+b)+k(a+c−b)+a−c a+b=0 a+c−b=1 a−c=0 a+a+a=1→a=(1/3) b=((−1)/3) c=(1/3) (1/3)∫(dk/(k−1))−(1/3)∫((k−1)/(k^2 +k+1))dk (1/3)∫(dk/(k−1))−(1/6)∫((2k+1−3)/(k^2 +k+1)) (1/3)∫(dk/(k−1))−(1/6)∫((d(k^2 +k+1))/(k^2 +k+1))+(1/2)∫(dk/((k+(1/2))^2 +(3/4))) =(1/3)ln(k−1)−(1/6)ln(k^2 +k+1)+(1/2)×(2/( (√3)))tan^(−1) (((k+(1/2))/((√3)/2)))+c =(1/3)ln{(1+t)^(1/3) −1}−(1/6)ln{(1+t)^(2/3) +(1+t)^(1/3) +1}+ (1/( (√3)))tan^(−1) {(((1+t)^(1/3) +(1/2))/((√3)/2))}+c pls put t=x^5
$$\int\frac{{dx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{5}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} }=\int\frac{{x}^{\mathrm{4}} }{{x}^{\mathrm{5}} \left(\mathrm{1}+{x}^{\mathrm{5}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{dx} \\ $$$${t}={x}^{\mathrm{5}} \:\:{dt}=\mathrm{5}{x}^{\mathrm{4}} {dx} \\ $$$$\int\frac{{dt}}{\mathrm{5}×{t}×\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dt}}{{t}\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$${k}^{\mathrm{3}} =\mathrm{1}+{t} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{3}{k}^{\mathrm{2}} {dk}}{\left({k}^{\mathrm{3}} −\mathrm{1}\right){k}} \\ $$$$\frac{\mathrm{3}}{\mathrm{5}}\int\frac{{kdk}}{\left({k}−\mathrm{1}\right)\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)} \\ $$$$\frac{{k}}{\left({k}−\mathrm{1}\right)\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}=\frac{{a}}{{k}−\mathrm{1}}+\frac{{bk}+{c}}{\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)} \\ $$$${k}={ak}^{\mathrm{2}} +{ak}+{a}+{bk}^{\mathrm{2}} +{ck}−{bk}−{c} \\ $$$${k}={k}^{\mathrm{2}} \left({a}+{b}\right)+{k}\left({a}+{c}−{b}\right)+{a}−{c} \\ $$$${a}+{b}=\mathrm{0} \\ $$$${a}+{c}−{b}=\mathrm{1} \\ $$$${a}−{c}=\mathrm{0} \\ $$$${a}+{a}+{a}=\mathrm{1}\rightarrow{a}=\frac{\mathrm{1}}{\mathrm{3}}\:\:{b}=\frac{−\mathrm{1}}{\mathrm{3}}\:\:\:{c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dk}}{{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{k}−\mathrm{1}}{{k}^{\mathrm{2}} +{k}+\mathrm{1}}{dk} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dk}}{{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{k}+\mathrm{1}−\mathrm{3}}{{k}^{\mathrm{2}} +{k}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dk}}{{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}{{k}^{\mathrm{2}} +{k}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dk}}{\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({k}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{k}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left\{\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{1}\right\}−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left\{\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{1}\right\}+ \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left\{\frac{\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right\}+{c} \\ $$$${pls}\:{put}\:{t}={x}^{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *