Menu Close

1-x-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 123037 by benjo_mathlover last updated on 22/Nov/20
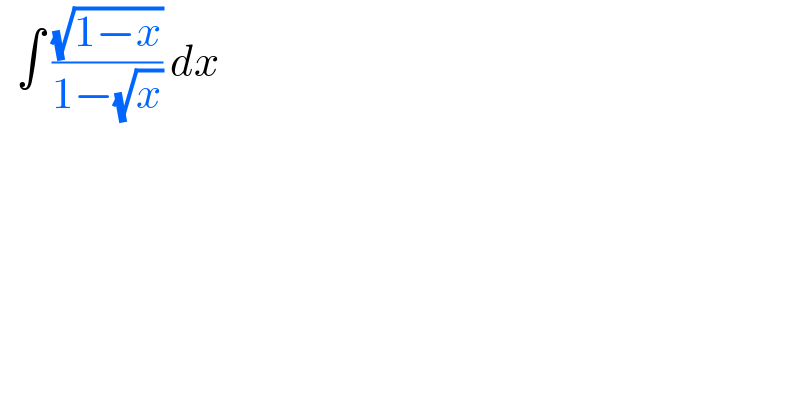
∫ ((√(1−x))/(1−(√x))) dx
$$\:\:\int\:\frac{\sqrt{\mathrm{1}−{x}}}{\mathrm{1}−\sqrt{{x}}}\:{dx} \\ $$$$ \\ $$
Answered by MJS_new last updated on 22/Nov/20
∫((√(1−x))/(1−(√x)))dx= [t=((√(1−x))/(1−(√x))) → dx=2(√x)(1−(√x))(√(1−x))] =8∫((t^2 (t^2 −1))/((t^2 +1)^3 ))dt= [Ostrogradski′s Method] =−((2t(3t^2 +1))/((t^2 +1)^2 ))+2∫(dt/(t^2 +1))= =−(2+(√x))(√(1−x))+2arctan ((√(1−x))/(1−(√x))) +C btw 2arctan ((√(1−x))/(1−(√x))) =−arcsin (√(1−x)) =−arccos (√x)
$$\int\frac{\sqrt{\mathrm{1}−{x}}}{\mathrm{1}−\sqrt{{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{1}−{x}}}{\mathrm{1}−\sqrt{{x}}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}\left(\mathrm{1}−\sqrt{{x}}\right)\sqrt{\mathrm{1}−{x}}\right] \\ $$$$=\mathrm{8}\int\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{\mathrm{2}{t}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=−\left(\mathrm{2}+\sqrt{{x}}\right)\sqrt{\mathrm{1}−{x}}+\mathrm{2arctan}\:\frac{\sqrt{\mathrm{1}−{x}}}{\mathrm{1}−\sqrt{{x}}}\:+{C} \\ $$$$\mathrm{btw}\:\mathrm{2arctan}\:\:\frac{\sqrt{\mathrm{1}−{x}}}{\mathrm{1}−\sqrt{{x}}}\:=−\mathrm{arcsin}\:\sqrt{\mathrm{1}−{x}}\:=−\mathrm{arccos}\:\sqrt{{x}} \\ $$
Answered by ajfour last updated on 22/Nov/20
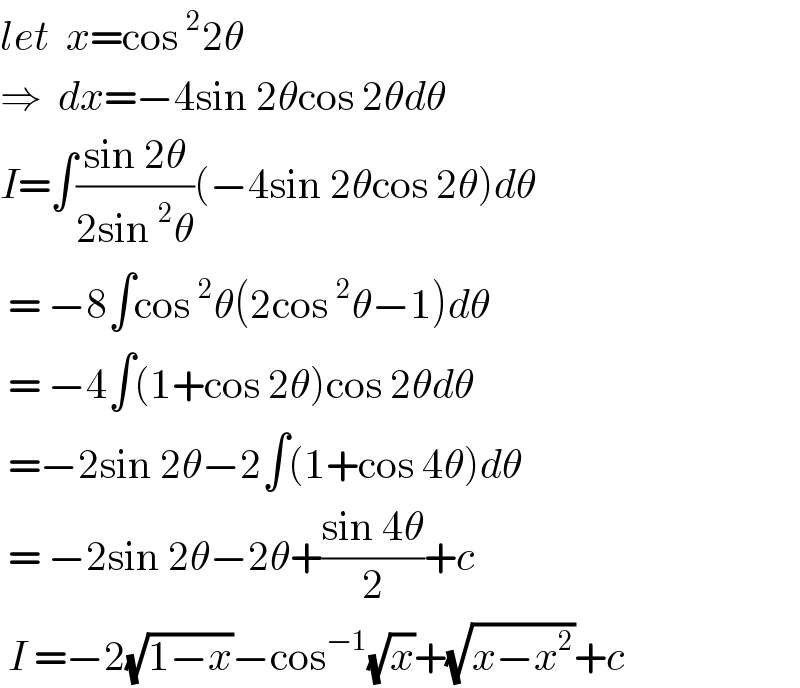
let x=cos^2 2θ ⇒ dx=−4sin 2θcos 2θdθ I=∫((sin 2θ)/(2sin^2 θ))(−4sin 2θcos 2θ)dθ = −8∫cos^2 θ(2cos^2 θ−1)dθ = −4∫(1+cos 2θ)cos 2θdθ =−2sin 2θ−2∫(1+cos 4θ)dθ = −2sin 2θ−2θ+((sin 4θ)/2)+c I =−2(√(1−x))−cos^(−1) (√x)+(√(x−x^2 ))+c
$${let}\:\:{x}=\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta \\ $$$$\Rightarrow\:\:{dx}=−\mathrm{4sin}\:\mathrm{2}\theta\mathrm{cos}\:\mathrm{2}\theta{d}\theta \\ $$$${I}=\int\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2sin}\:^{\mathrm{2}} \theta}\left(−\mathrm{4sin}\:\mathrm{2}\theta\mathrm{cos}\:\mathrm{2}\theta\right){d}\theta \\ $$$$\:=\:−\mathrm{8}\int\mathrm{cos}\:^{\mathrm{2}} \theta\left(\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}\right){d}\theta \\ $$$$\:=\:−\mathrm{4}\int\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)\mathrm{cos}\:\mathrm{2}\theta{d}\theta \\ $$$$\:=−\mathrm{2sin}\:\mathrm{2}\theta−\mathrm{2}\int\left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}\theta\right){d}\theta \\ $$$$\:=\:−\mathrm{2sin}\:\mathrm{2}\theta−\mathrm{2}\theta+\frac{\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{2}}+{c} \\ $$$$\:{I}\:=−\mathrm{2}\sqrt{\mathrm{1}−{x}}−\mathrm{cos}^{−\mathrm{1}} \sqrt{{x}}+\sqrt{{x}−{x}^{\mathrm{2}} }+{c} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Nov/20
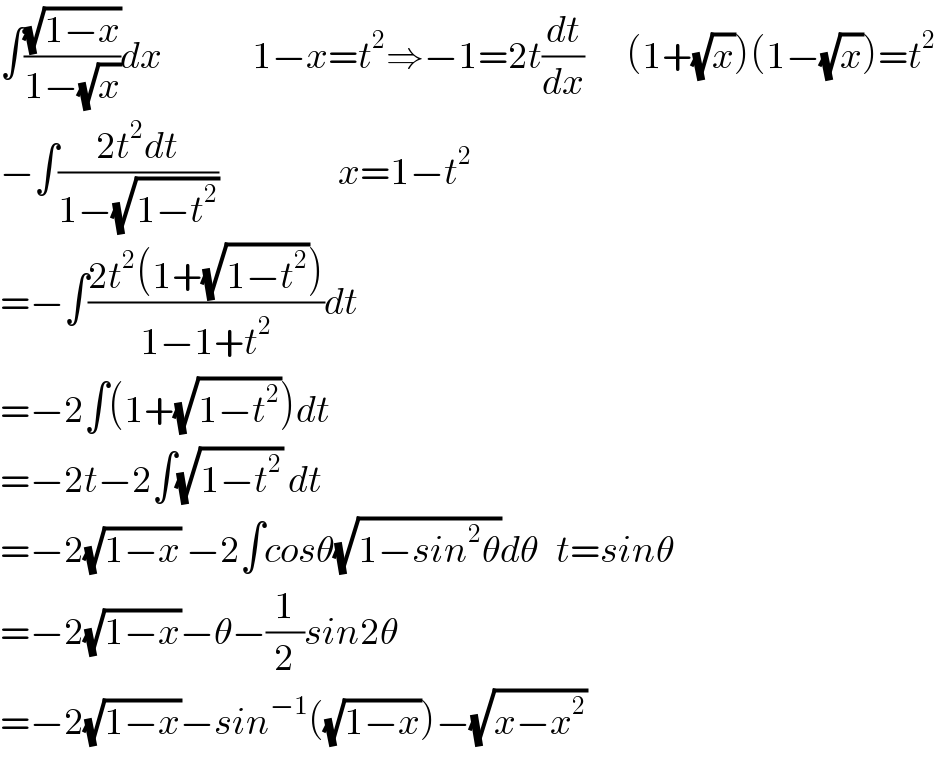
∫((√(1−x))/(1−(√x)))dx 1−x=t^2 ⇒−1=2t(dt/dx) (1+(√x))(1−(√x))=t^2 −∫((2t^2 dt)/(1−(√(1−t^2 )))) x=1−t^2 =−∫((2t^2 (1+(√(1−t^2 ))))/(1−1+t^2 ))dt =−2∫(1+(√(1−t^2 )))dt =−2t−2∫(√(1−t^2 )) dt =−2(√(1−x)) −2∫cosθ(√(1−sin^2 θ))dθ t=sinθ =−2(√(1−x))−θ−(1/2)sin2θ =−2(√(1−x))−sin^(−1) ((√(1−x)))−(√(x−x^2 ))
$$\int\frac{\sqrt{\mathrm{1}−{x}}}{\mathrm{1}−\sqrt{{x}}}{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}−{x}={t}^{\mathrm{2}} \Rightarrow−\mathrm{1}=\mathrm{2}{t}\frac{{dt}}{{dx}}\:\:\:\:\:\:\:\left(\mathrm{1}+\sqrt{{x}}\right)\left(\mathrm{1}−\sqrt{{x}}\right)={t}^{\mathrm{2}} \\ $$$$−\int\frac{\mathrm{2}{t}^{\mathrm{2}} {dt}}{\mathrm{1}−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{1}−{t}^{\mathrm{2}} \:\:\:\:\: \\ $$$$=−\int\frac{\mathrm{2}{t}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\right)}{\mathrm{1}−\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=−\mathrm{2}\int\left(\mathrm{1}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\right){dt} \\ $$$$=−\mathrm{2}{t}−\mathrm{2}\int\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt} \\ $$$$=−\mathrm{2}\sqrt{\mathrm{1}−{x}}\:−\mathrm{2}\int{cos}\theta\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \theta}{d}\theta\:\:\:{t}={sin}\theta \\ $$$$=−\mathrm{2}\sqrt{\mathrm{1}−{x}}−\theta−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta \\ $$$$=−\mathrm{2}\sqrt{\mathrm{1}−{x}}−{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−{x}}\right)−\sqrt{{x}−{x}^{\mathrm{2}} }\: \\ $$
Answered by liberty last updated on 23/Nov/20
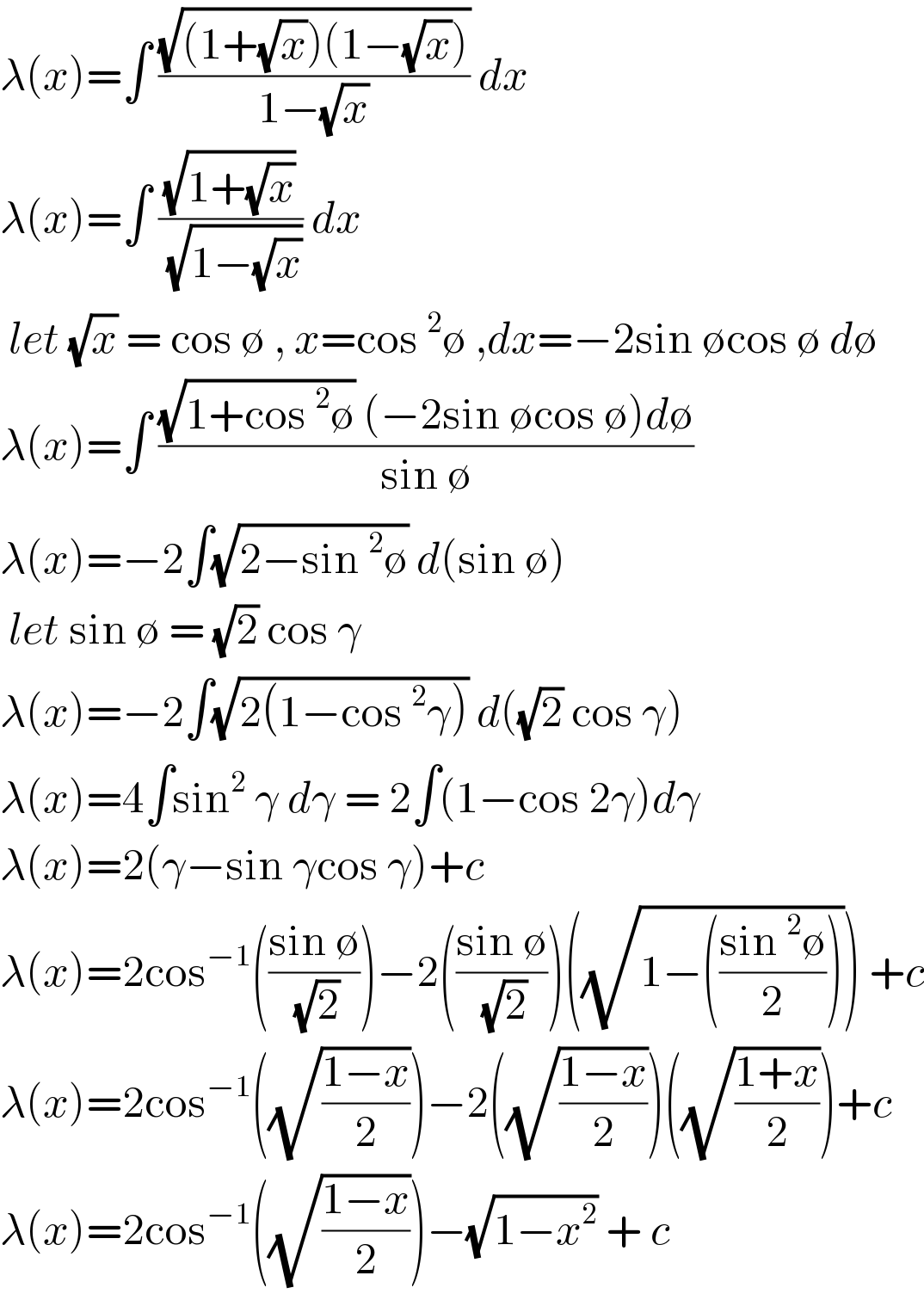
λ(x)=∫ ((√((1+(√x))(1−(√x))))/(1−(√x))) dx λ(x)=∫ ((√(1+(√x)))/( (√(1−(√x))))) dx let (√x) = cos ∅ , x=cos^2 ∅ ,dx=−2sin ∅cos ∅ d∅ λ(x)=∫ (((√(1+cos^2 ∅)) (−2sin ∅cos ∅)d∅)/(sin ∅)) λ(x)=−2∫(√(2−sin^2 ∅)) d(sin ∅) let sin ∅ = (√2) cos γ λ(x)=−2∫(√(2(1−cos^2 γ))) d((√2) cos γ) λ(x)=4∫sin^2 γ dγ = 2∫(1−cos 2γ)dγ λ(x)=2(γ−sin γcos γ)+c λ(x)=2cos^(−1) (((sin ∅)/( (√2))))−2(((sin ∅)/( (√2))))((√(1−(((sin^2 ∅)/2))))) +c λ(x)=2cos^(−1) ((√((1−x)/2)))−2((√((1−x)/2)))((√((1+x)/2)))+c λ(x)=2cos^(−1) ((√((1−x)/2)))−(√(1−x^2 )) + c
$$\lambda\left({x}\right)=\int\:\frac{\sqrt{\left(\mathrm{1}+\sqrt{{x}}\right)\left(\mathrm{1}−\sqrt{{x}}\right)}}{\mathrm{1}−\sqrt{{x}}}\:{dx}\: \\ $$$$\lambda\left({x}\right)=\int\:\frac{\sqrt{\mathrm{1}+\sqrt{{x}}}}{\:\sqrt{\mathrm{1}−\sqrt{{x}}}}\:{dx}\: \\ $$$$\:{let}\:\sqrt{{x}}\:=\:\mathrm{cos}\:\emptyset\:,\:{x}=\mathrm{cos}\:^{\mathrm{2}} \emptyset\:,{dx}=−\mathrm{2sin}\:\emptyset\mathrm{cos}\:\emptyset\:{d}\emptyset \\ $$$$\lambda\left({x}\right)=\int\:\frac{\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \emptyset}\:\left(−\mathrm{2sin}\:\emptyset\mathrm{cos}\:\emptyset\right){d}\emptyset}{\mathrm{sin}\:\emptyset} \\ $$$$\lambda\left({x}\right)=−\mathrm{2}\int\sqrt{\mathrm{2}−\mathrm{sin}\:^{\mathrm{2}} \emptyset}\:{d}\left(\mathrm{sin}\:\emptyset\right)\: \\ $$$$\:{let}\:\mathrm{sin}\:\emptyset\:=\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\gamma\: \\ $$$$\lambda\left({x}\right)=−\mathrm{2}\int\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \gamma\right)}\:{d}\left(\sqrt{\mathrm{2}}\:\mathrm{cos}\:\gamma\right) \\ $$$$\lambda\left({x}\right)=\mathrm{4}\int\mathrm{sin}^{\mathrm{2}} \:\gamma\:{d}\gamma\:=\:\mathrm{2}\int\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\gamma\right){d}\gamma \\ $$$$\lambda\left({x}\right)=\mathrm{2}\left(\gamma−\mathrm{sin}\:\gamma\mathrm{cos}\:\gamma\right)+{c} \\ $$$$\lambda\left({x}\right)=\mathrm{2cos}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\emptyset}{\:\sqrt{\mathrm{2}}}\right)−\mathrm{2}\left(\frac{\mathrm{sin}\:\emptyset}{\:\sqrt{\mathrm{2}}}\right)\left(\sqrt{\mathrm{1}−\left(\frac{\mathrm{sin}\:^{\mathrm{2}} \emptyset}{\mathrm{2}}\right)}\right)\:+{c} \\ $$$$\lambda\left({x}\right)=\mathrm{2cos}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{2}}}\right)−\mathrm{2}\left(\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{2}}}\right)\left(\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{2}}}\right)+{c} \\ $$$$\lambda\left({x}\right)=\mathrm{2cos}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{2}}}\right)−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\:{c}\: \\ $$
Answered by mathmax by abdo last updated on 22/Nov/20
I =∫ ((√(1−x))/(1−(√x))) dx changement (√x)=t give x=t^2 ⇒ I =∫ ((√(1−t^2 ))/(1−t))(2t)dt =−2 ∫ (((√(1−t^2 ))t)/(t−1)) dt =−2 ∫ (((t−1+1)(√(1−t^2 )))/(t−1))dt =−2 ∫(√(1−t^2 ))dt −2 ∫ ((√(1−t^2 ))/(t−1))dt ∫ (√(1−t^2 ))dt =_(t=sinθ) ∫ cosθ cosθ dθ =∫ ((1+cos(2θ))/2)dθ =(θ/2) +(1/4)sin(2θ)+c_1 =(θ/2) +(1/2)sinθ cosθ +c_1 =((arcsint)/2) +(t/2)(√(1−t^2 )) +c_1 −2∫ ((√(1−t^2 ))/(t−1))dt =2 ∫(√((1−t^2 )/((1−t)^2 )))dt =2 ∫(√(((1−t)(1+t))/((1−t)^2 )))dt =2 ∫(√((1+t)/(1−t)))dt =_(t=cosu) 2 ∫ (√((((2cos^2 ((u/2)))/(2sin^2 ((u/2))))())−sinu du) =−2 ∫ ((cos((u/2)))/(sin((u/2))))(2cos((u/2))sin((u/2)))du =−4 ∫ cos^2 ((u/2))du =−4∫((1+cosu)/2)du =−2u−2 ∫ cosu du =−2u−2sinu +c_2 =−2arcost−2(√(1−t^2 )) +c_2 ⇒ I =−arcsint−t(√(1−t^2 )) −2arcost −2(√(1−t^2 )) +C
$$\mathrm{I}\:=\int\:\frac{\sqrt{\mathrm{1}−\mathrm{x}}}{\mathrm{1}−\sqrt{\mathrm{x}}}\:\mathrm{dx}\:\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{1}−\mathrm{t}}\left(\mathrm{2t}\right)\mathrm{dt}\:=−\mathrm{2}\:\int\:\frac{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{t}}{\mathrm{t}−\mathrm{1}}\:\mathrm{dt} \\ $$$$=−\mathrm{2}\:\int\:\:\frac{\left(\mathrm{t}−\mathrm{1}+\mathrm{1}\right)\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}−\mathrm{1}}\mathrm{dt}\:=−\mathrm{2}\:\int\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:−\mathrm{2}\:\int\:\:\frac{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}−\mathrm{1}}\mathrm{dt} \\ $$$$\int\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=_{\mathrm{t}=\mathrm{sin}\theta} \:\:\:\int\:\mathrm{cos}\theta\:\mathrm{cos}\theta\:\mathrm{d}\theta\:=\int\:\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\mathrm{d}\theta \\ $$$$=\frac{\theta}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2}\theta\right)+\mathrm{c}_{\mathrm{1}} \:=\frac{\theta}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\theta\:\mathrm{cos}\theta\:+\mathrm{c}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{arcsint}}{\mathrm{2}}\:+\frac{\mathrm{t}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:+\mathrm{c}_{\mathrm{1}} \\ $$$$−\mathrm{2}\int\:\:\frac{\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}−\mathrm{1}}\mathrm{dt}\:=\mathrm{2}\:\int\sqrt{\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }}\mathrm{dt}\:=\mathrm{2}\:\int\sqrt{\frac{\left(\mathrm{1}−\mathrm{t}\right)\left(\mathrm{1}+\mathrm{t}\right)}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }}\mathrm{dt} \\ $$$$\left.=\mathrm{2}\:\int\sqrt{\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}}\mathrm{dt}\:=_{\mathrm{t}=\mathrm{cosu}} \:\:\:\mathrm{2}\:\int\:\sqrt{\left(\frac{\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{u}}{\mathrm{2}}\right)}{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{u}}{\mathrm{2}}\right)}\left(\right.\right.}−\mathrm{sinu}\:\mathrm{du}\right) \\ $$$$=−\mathrm{2}\:\int\:\:\:\frac{\mathrm{cos}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)}\left(\mathrm{2cos}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{du} \\ $$$$=−\mathrm{4}\:\int\:\:\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{u}}{\mathrm{2}}\right)\mathrm{du}\:=−\mathrm{4}\int\frac{\mathrm{1}+\mathrm{cosu}}{\mathrm{2}}\mathrm{du}\:=−\mathrm{2u}−\mathrm{2}\:\int\:\mathrm{cosu}\:\mathrm{du} \\ $$$$=−\mathrm{2u}−\mathrm{2sinu}\:+\mathrm{c}_{\mathrm{2}} =−\mathrm{2arcost}−\mathrm{2}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:+\mathrm{c}_{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=−\mathrm{arcsint}−\mathrm{t}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:−\mathrm{2arcost}\:−\mathrm{2}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *