Question Number 166398 by mathlove last updated on 19/Feb/22
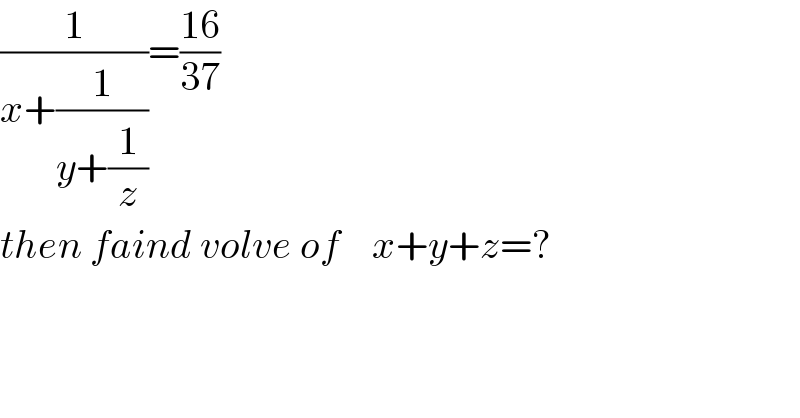
$$\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{y}+\frac{\mathrm{1}}{{z}}}}=\frac{\mathrm{16}}{\mathrm{37}} \\ $$$${then}\:{faind}\:{volve}\:{of}\:\:\:\:{x}+{y}+{z}=? \\ $$
Answered by floor(10²Eta[1]) last updated on 19/Feb/22
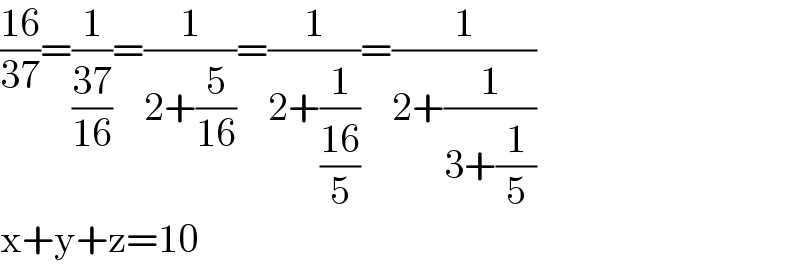
$$\frac{\mathrm{16}}{\mathrm{37}}=\frac{\mathrm{1}}{\frac{\mathrm{37}}{\mathrm{16}}}=\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{5}}{\mathrm{16}}}=\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\frac{\mathrm{16}}{\mathrm{5}}}}=\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{5}}}} \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{10} \\ $$
