Question Number 99044 by mashallah last updated on 18/Jun/20

$$\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}=? \\ $$
Answered by bemath last updated on 18/Jun/20

$$\mathrm{arc}\:\mathrm{tan}\:\mathrm{x}\:+\:\mathrm{c} \\ $$
Answered by Mr.D.N. last updated on 18/Jun/20
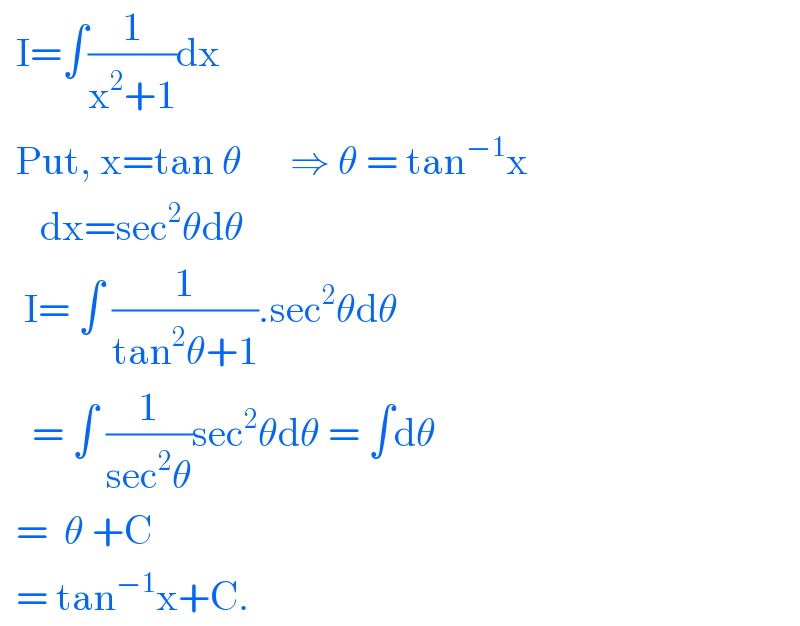
$$\:\:\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\mathrm{Put},\:\mathrm{x}=\mathrm{tan}\:\theta\:\:\:\:\:\:\Rightarrow\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x} \\ $$$$\:\:\:\:\:\mathrm{dx}=\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:\mathrm{I}=\:\int\:\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{1}}.\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:\:=\:\int\:\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{2}} \theta}\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta\:=\:\int\mathrm{d}\theta \\ $$$$\:\:=\:\:\theta\:+\mathrm{C} \\ $$$$\:\:=\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x}+\mathrm{C}. \\ $$
Answered by abdomathmax last updated on 18/Jun/20
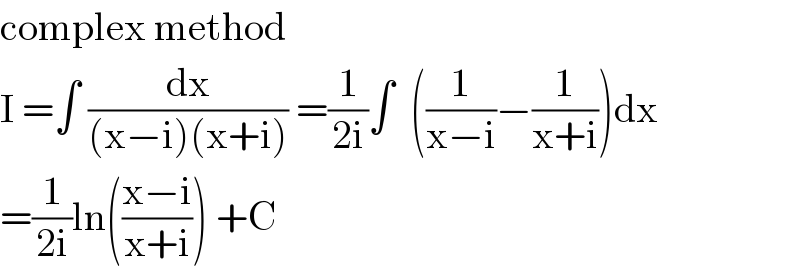
$$\mathrm{complex}\:\mathrm{method}\: \\ $$$$\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{i}\right)\left(\mathrm{x}+\mathrm{i}\right)}\:=\frac{\mathrm{1}}{\mathrm{2i}}\int\:\:\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{i}}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{\mathrm{x}−\mathrm{i}}{\mathrm{x}+\mathrm{i}}\right)\:+\mathrm{C} \\ $$
Commented by abdomathmax last updated on 18/Jun/20
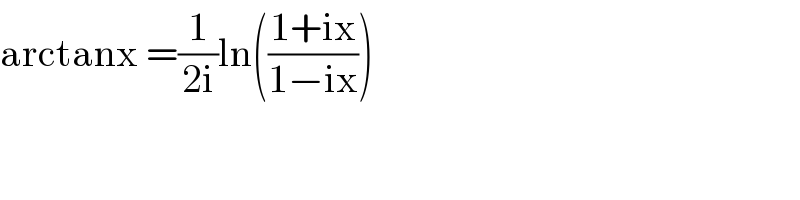
$$\mathrm{arctanx}\:=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{ix}}{\mathrm{1}−\mathrm{ix}}\right) \\ $$
