Menu Close

1-x-2-2-x-4-8x-2-4-dx-2-Shortest-distance-between-the-parabolas-y-2-4x-and-y-2-2x-6-is-

Tinku Tara 0 Comments
Pin




Question Number 58478 by rahul 19 last updated on 23/Apr/19
{1} ∫((x^2 −2)/(x^4 +8x^2 +4)) dx = ? {2} Shortest distance between the parabolas y^2 =4x and y^2 =2x−6 is ?
$$\left\{\mathrm{1}\right\}\:\:\:\int\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{2}} +\mathrm{4}}\:{dx}\:=\:? \\ $$$$\left\{\mathrm{2}\right\}\:\:{Shortest}\:{distance}\:{between}\:{the} \\ $$$${parabolas}\:{y}^{\mathrm{2}} =\mathrm{4}{x}\:{and}\:{y}^{\mathrm{2}} =\mathrm{2}{x}−\mathrm{6}\:{is}\:? \\ $$
Commented by maxmathsup by imad last updated on 24/Apr/19
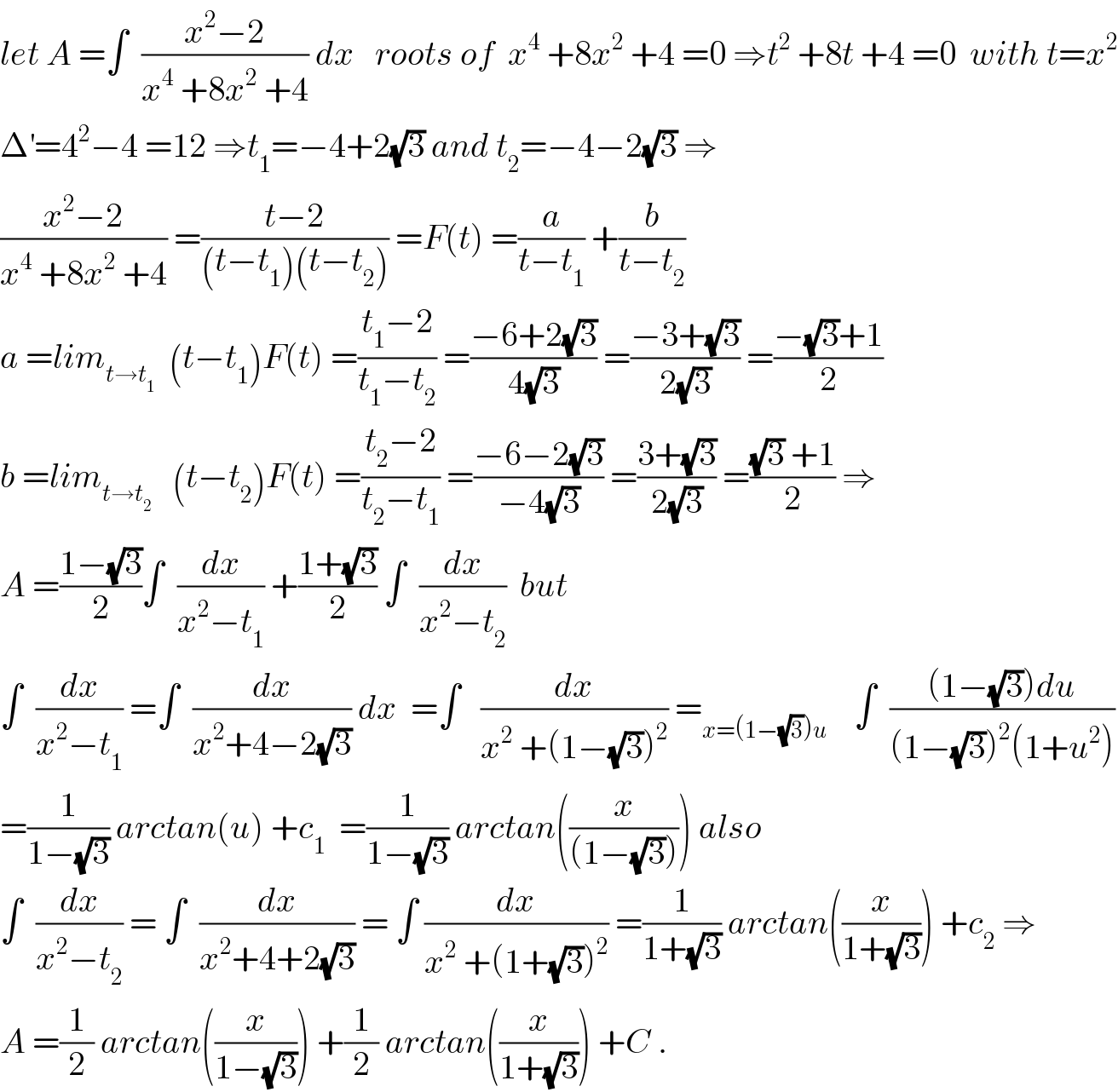
let A =∫ ((x^2 −2)/(x^4 +8x^2 +4)) dx roots of x^4 +8x^2 +4 =0 ⇒t^2 +8t +4 =0 with t=x^2 Δ^′ =4^2 −4 =12 ⇒t_1 =−4+2(√3) and t_2 =−4−2(√3) ⇒ ((x^2 −2)/(x^4 +8x^2 +4)) =((t−2)/((t−t_1 )(t−t_2 ))) =F(t) =(a/(t−t_1 )) +(b/(t−t_2 )) a =lim_(t→t_1 ) (t−t_1 )F(t) =((t_1 −2)/(t_1 −t_2 )) =((−6+2(√3))/(4(√3))) =((−3+(√3))/(2(√3))) =((−(√3)+1)/2) b =lim_(t→t_2 ) (t−t_2 )F(t) =((t_2 −2)/(t_2 −t_1 )) =((−6−2(√3))/(−4(√3))) =((3+(√3))/(2(√3))) =(((√3) +1)/2) ⇒ A =((1−(√3))/2)∫ (dx/(x^2 −t_1 )) +((1+(√3))/2) ∫ (dx/(x^2 −t_2 )) but ∫ (dx/(x^2 −t_1 )) =∫ (dx/(x^2 +4−2(√3))) dx =∫ (dx/(x^2 +(1−(√3))^2 )) =_(x=(1−(√3))u) ∫ (((1−(√3))du)/((1−(√3))^2 (1+u^2 ))) =(1/(1−(√3))) arctan(u) +c_1 =(1/(1−(√3))) arctan((x/((1−(√3))))) also ∫ (dx/(x^2 −t_2 )) = ∫ (dx/(x^2 +4+2(√3))) = ∫ (dx/(x^2 +(1+(√3))^2 )) =(1/(1+(√3))) arctan((x/(1+(√3)))) +c_2 ⇒ A =(1/2) arctan((x/(1−(√3)))) +(1/2) arctan((x/(1+(√3)))) +C .
$${let}\:{A}\:=\int\:\:\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} \:+\mathrm{8}{x}^{\mathrm{2}} \:+\mathrm{4}}\:{dx}\:\:\:{roots}\:{of}\:\:{x}^{\mathrm{4}} \:+\mathrm{8}{x}^{\mathrm{2}} \:+\mathrm{4}\:=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} \:+\mathrm{8}{t}\:+\mathrm{4}\:=\mathrm{0}\:\:{with}\:{t}={x}^{\mathrm{2}} \\ $$$$\Delta^{'} =\mathrm{4}^{\mathrm{2}} −\mathrm{4}\:=\mathrm{12}\:\Rightarrow{t}_{\mathrm{1}} =−\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\:{and}\:{t}_{\mathrm{2}} =−\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\Rightarrow \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{2}}{{x}^{\mathrm{4}} \:+\mathrm{8}{x}^{\mathrm{2}} \:+\mathrm{4}}\:=\frac{{t}−\mathrm{2}}{\left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)}\:={F}\left({t}\right)\:=\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} } \\ $$$${a}\:={lim}_{{t}\rightarrow{t}_{\mathrm{1}} } \:\:\left({t}−{t}_{\mathrm{1}} \right){F}\left({t}\right)\:=\frac{{t}_{\mathrm{1}} −\mathrm{2}}{{t}_{\mathrm{1}} −{t}_{\mathrm{2}} }\:=\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}\sqrt{\mathrm{3}}}\:=\frac{−\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\frac{−\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}} \\ $$$${b}\:={lim}_{{t}\rightarrow{t}_{\mathrm{2}} } \:\:\:\left({t}−{t}_{\mathrm{2}} \right){F}\left({t}\right)\:=\frac{{t}_{\mathrm{2}} −\mathrm{2}}{{t}_{\mathrm{2}} −{t}_{\mathrm{1}} }\:=\frac{−\mathrm{6}−\mathrm{2}\sqrt{\mathrm{3}}}{−\mathrm{4}\sqrt{\mathrm{3}}}\:=\frac{\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{3}}}\:=\frac{\sqrt{\mathrm{3}}\:+\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{t}_{\mathrm{1}} }\:+\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{t}_{\mathrm{2}} }\:\:{but} \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{t}_{\mathrm{1}} }\:=\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}\:{dx}\:\:=\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:=_{{x}=\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){u}} \:\:\:\:\int\:\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){du}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\sqrt{\mathrm{3}}}\:{arctan}\left({u}\right)\:+{c}_{\mathrm{1}} \:\:=\frac{\mathrm{1}}{\mathrm{1}−\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{{x}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)}\right)\:{also} \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{t}_{\mathrm{2}} }\:=\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\int\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{3}}}\right)\:+{c}_{\mathrm{2}} \:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{{x}}{\mathrm{1}−\sqrt{\mathrm{3}}}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{3}}}\right)\:+{C}\:. \\ $$
Answered by Prithwish sen last updated on 23/Apr/19
∫((x^2 −2)/(x^4 +8x^2 +4))dx =∫(((1−(2/x^2 )))/(x^2 +(4/x^2 )+8))dx =∫((d(x+(2/x)))/((x+(2/x))^2 +4)) =(1/2)tan^(−1) ∣((x^2 +2)/(2x))∣+C
$$\int\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}^{\mathrm{4}} +\mathrm{8x}^{\mathrm{2}} +\mathrm{4}}\mathrm{dx} \\ $$$$=\int\frac{\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{8}}\mathrm{dx} \\ $$$$=\int\frac{\mathrm{d}\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)}{\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \mid\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2x}}\mid+\mathrm{C} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 24/Apr/19
thank u sir.
$${thank}\:{u}\:{sir}. \\ $$
Answered by mr W last updated on 23/Apr/19
(2) from point ((h^2 /4),h) to point (((k^2 +6)/2),k): D=d^2 =((h^2 /4)−((k^2 +6)/2))^2 +(h−k)^2 (∂D/∂h)=2((h^2 /4)−((k^2 +6)/2))((2h)/4)+2(h−k)=0 ⇒((h^2 /4)−((k^2 +6)/2))(h/2)+(h−k)=0 ...(i) (∂D/∂k)=−2((h^2 /4)−((k^2 +6)/2))((2k)/2)−2(h−k)=0 ⇒((h^2 /4)−((k^2 +6)/2))k+(h−k)=0 ...(ii) from (i) and (ii): ⇒k=(h/2) ⇒(h^2 /8)=2 ⇒h=±4⇒point (4,±4) ⇒k=±2⇒point (5,±2) min. d=(√D_(min) )=(√((5−4)^2 +(2−4)^2 ))=(√5)
$$\left(\mathrm{2}\right) \\ $$$${from}\:{point}\:\left(\frac{{h}^{\mathrm{2}} }{\mathrm{4}},{h}\right)\:{to}\:{point}\:\left(\frac{{k}^{\mathrm{2}} +\mathrm{6}}{\mathrm{2}},{k}\right): \\ $$$${D}={d}^{\mathrm{2}} =\left(\frac{{h}^{\mathrm{2}} }{\mathrm{4}}−\frac{{k}^{\mathrm{2}} +\mathrm{6}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({h}−{k}\right)^{\mathrm{2}} \\ $$$$\frac{\partial{D}}{\partial{h}}=\mathrm{2}\left(\frac{{h}^{\mathrm{2}} }{\mathrm{4}}−\frac{{k}^{\mathrm{2}} +\mathrm{6}}{\mathrm{2}}\right)\frac{\mathrm{2}{h}}{\mathrm{4}}+\mathrm{2}\left({h}−{k}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{{h}^{\mathrm{2}} }{\mathrm{4}}−\frac{{k}^{\mathrm{2}} +\mathrm{6}}{\mathrm{2}}\right)\frac{{h}}{\mathrm{2}}+\left({h}−{k}\right)=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial{D}}{\partial{k}}=−\mathrm{2}\left(\frac{{h}^{\mathrm{2}} }{\mathrm{4}}−\frac{{k}^{\mathrm{2}} +\mathrm{6}}{\mathrm{2}}\right)\frac{\mathrm{2}{k}}{\mathrm{2}}−\mathrm{2}\left({h}−{k}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{{h}^{\mathrm{2}} }{\mathrm{4}}−\frac{{k}^{\mathrm{2}} +\mathrm{6}}{\mathrm{2}}\right){k}+\left({h}−{k}\right)=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\Rightarrow{k}=\frac{{h}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{h}^{\mathrm{2}} }{\mathrm{8}}=\mathrm{2} \\ $$$$\Rightarrow{h}=\pm\mathrm{4}\Rightarrow{point}\:\left(\mathrm{4},\pm\mathrm{4}\right) \\ $$$$\Rightarrow{k}=\pm\mathrm{2}\Rightarrow{point}\:\left(\mathrm{5},\pm\mathrm{2}\right) \\ $$$${min}.\:{d}=\sqrt{{D}_{{min}} }=\sqrt{\left(\mathrm{5}−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{2}−\mathrm{4}\right)^{\mathrm{2}} }=\sqrt{\mathrm{5}} \\ $$
Commented by rahul 19 last updated on 24/Apr/19
thank U sir.
$${thank}\:{U}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *