Question Number 83327 by john santu last updated on 01/Mar/20
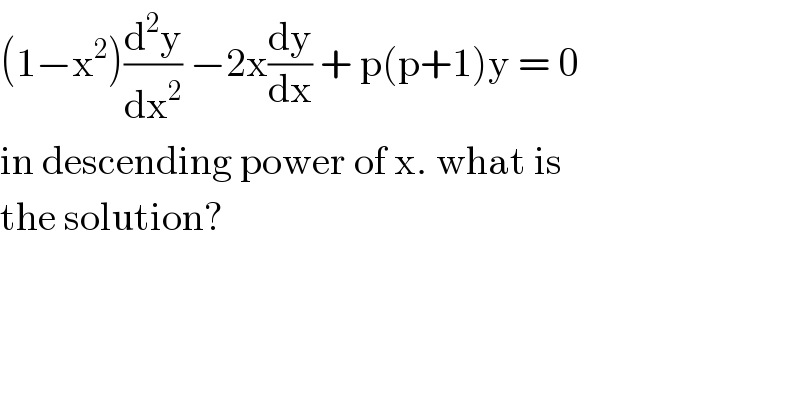
$$\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:−\mathrm{2x}\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\mathrm{y}\:=\:\mathrm{0}\: \\ $$$$\mathrm{in}\:\mathrm{descending}\:\mathrm{power}\:\mathrm{of}\:\mathrm{x}.\:\mathrm{what}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{solution}? \\ $$
Commented by Joel578 last updated on 01/Mar/20

$$\mathrm{It}\:\mathrm{is}\:\mathrm{Legendre}'\mathrm{s}\:\mathrm{equation}. \\ $$$$\mathrm{Its}\:\:\mathrm{solutions}\:\:\mathrm{known}\:\mathrm{as}\:\mathrm{Legendre}\:\mathrm{polynomial} \\ $$$$ \\ $$
Commented by niroj last updated on 01/Mar/20
![(1−x^2 )(d^2 y/dx^2 )−2x(dy/dx)+p(p+1)y=0....(i) Sol^n : let, x=0 , f(x)≠0 i.e. x=0 is ordinary point i.e. solution of equation is y= Σ_(r=0) ^∞ a_r x^r (dy/dx)= Σ_(r=0) ^∞ a_r rx^(r−1) (d^2 y/dx^2 ) = Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) Put, the value of y,y_1 and y_2 in eq^n (i) (1−x^2 )Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −2xΣ_(r=0) ^∞ a_r rx^(r−1) +p(p+1)Σ_(r=0) ^∞ a_r x^r =0 or, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r r(r−1)x^r −2Σ_(r=0) ^∞ a_r rx^r +p(p+1)Σ_(r=0) ^∞ a_r x^r =0 or, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r [r(r−1)+2r−p(p+1)]x^r =0 or_, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r [r^2 +r−p(p+1)]x^r =0 or_(, ) Σ_(r=0) ^∞ a_r [(r^2 −r)x^(r−2) −(r^2 +r−p^2 −p)]x^r =0 or,a_r r(r−1)x^(r−2) −a_r [r(r+1)−p(p+1)]x^r =0 put r=r+2 a_(r+2) (r+2)(r+1)x^r −a_r [(r+2)(r+3)−p(p+1)]x^r =0 or, [a_(r+2) (r+2)(r+1)−a_r {(r+2)(r+3)−p(p+1)}]x^r =0 or, a_(r+2) (r+2)(r+1)−a_r {(r+2)(r+3)−p(p+1)}=0 a_(r+2) = (((r+2)(r+3)−p(p+1))/((r+2)(r+1)))a_r put r=0, a_2 = ((2.3−p(p+1))/(2.1))a_0 then put descending value of r in terms of power series y= Σ_(r=0) ^∞ a_r x^r = a_0 +ax+a_2 x^2 +....](https://www.tinkutara.com/question/Q83384.png)
$$\:\left(\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }−\mathrm{2}\boldsymbol{\mathrm{x}}\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}+\boldsymbol{\mathrm{p}}\left(\boldsymbol{\mathrm{p}}+\mathrm{1}\right)\boldsymbol{\mathrm{y}}=\mathrm{0}….\left(\mathrm{i}\right) \\ $$$$\:\mathrm{Sol}^{\mathrm{n}} : \\ $$$$\:\:\:\:\mathrm{let},\:\boldsymbol{\mathrm{x}}=\mathrm{0}\:,\:\mathrm{f}\left(\mathrm{x}\right)\neq\mathrm{0} \\ $$$$\:\mathrm{i}.\mathrm{e}.\:\mathrm{x}=\mathrm{0}\:\mathrm{is}\:\:\mathrm{ordinary}\:\mathrm{point} \\ $$$$\:\mathrm{i}.\mathrm{e}.\:\mathrm{solution}\:\mathrm{of}\:\mathrm{equation}\:\mathrm{is} \\ $$$$\:\:\:\mathrm{y}=\:\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\:\mathrm{a}_{\mathrm{r}} \:\mathrm{x}^{\mathrm{r}} \\ $$$$\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\:\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{rx}^{\mathrm{r}−\mathrm{1}} \\ $$$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\:\mathrm{a}_{\mathrm{r}} \mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)\mathrm{x}^{\mathrm{r}−\mathrm{2}} \\ $$$$\: \\ $$$$\:\mathrm{Put},\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{y},\mathrm{y}_{\mathrm{1}} \mathrm{and}\:\mathrm{y}_{\mathrm{2}} \:\mathrm{in}\:\mathrm{eq}^{\mathrm{n}} \left(\mathrm{i}\right) \\ $$$$\:\:\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)\mathrm{x}^{\mathrm{r}−\mathrm{2}} −\mathrm{2x}\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{rx}^{\mathrm{r}−\mathrm{1}} +\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}} \:=\mathrm{0} \\ $$$$\mathrm{or},\:\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)\mathrm{x}^{\mathrm{r}−\mathrm{2}} −\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)\mathrm{x}^{\mathrm{r}} −\mathrm{2}\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{rx}^{\mathrm{r}} +\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}} =\mathrm{0} \\ $$$$\:\mathrm{or},\:\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)\mathrm{x}^{\mathrm{r}−\mathrm{2}} −\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \left[\mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)+\mathrm{2r}−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\right]\mathrm{x}^{\mathrm{r}} =\mathrm{0} \\ $$$$\:\mathrm{or}_{,} \:\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)\mathrm{x}^{\mathrm{r}−\mathrm{2}} −\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \left[\mathrm{r}^{\mathrm{2}} +\mathrm{r}−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\right]\mathrm{x}^{\mathrm{r}} =\mathrm{0} \\ $$$$\:\mathrm{or}_{,\:} \underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \left[\left(\mathrm{r}^{\mathrm{2}} −\mathrm{r}\right)\mathrm{x}^{\mathrm{r}−\mathrm{2}} −\left(\mathrm{r}^{\mathrm{2}} +\mathrm{r}−\mathrm{p}^{\mathrm{2}} −\mathrm{p}\right)\right]\mathrm{x}^{\mathrm{r}} =\mathrm{0} \\ $$$$\:\mathrm{or},\mathrm{a}_{\mathrm{r}} \mathrm{r}\left(\mathrm{r}−\mathrm{1}\right)\mathrm{x}^{\mathrm{r}−\mathrm{2}} −\mathrm{a}_{\mathrm{r}} \left[\mathrm{r}\left(\mathrm{r}+\mathrm{1}\right)−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\right]\mathrm{x}^{\mathrm{r}} =\mathrm{0} \\ $$$$\mathrm{put}\:\mathrm{r}=\mathrm{r}+\mathrm{2} \\ $$$$\:\:\mathrm{a}_{\mathrm{r}+\mathrm{2}} \:\left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{1}\right)\mathrm{x}^{\mathrm{r}} −\mathrm{a}_{\mathrm{r}} \left[\left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{3}\right)−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\right]\mathrm{x}^{\mathrm{r}} =\mathrm{0} \\ $$$$\:\mathrm{or},\:\left[\mathrm{a}_{\mathrm{r}+\mathrm{2}} \left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{1}\right)−\mathrm{a}_{\mathrm{r}} \left\{\left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{3}\right)−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\right\}\right]\mathrm{x}^{\mathrm{r}} =\mathrm{0} \\ $$$$\:\mathrm{or},\:\:\mathrm{a}_{\mathrm{r}+\mathrm{2}} \left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{1}\right)−\mathrm{a}_{\mathrm{r}} \left\{\left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{3}\right)−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)\right\}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{a}_{\mathrm{r}+\mathrm{2}} \:=\:\frac{\left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{3}\right)−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)}{\left(\mathrm{r}+\mathrm{2}\right)\left(\mathrm{r}+\mathrm{1}\right)}\mathrm{a}_{\mathrm{r}} \\ $$$$\:\mathrm{put}\:\mathrm{r}=\mathrm{0},\:\:\:\:\mathrm{a}_{\mathrm{2}} =\:\frac{\mathrm{2}.\mathrm{3}−\mathrm{p}\left(\mathrm{p}+\mathrm{1}\right)}{\mathrm{2}.\mathrm{1}}\mathrm{a}_{\mathrm{0}} \\ $$$$\:\:\mathrm{then}\:\mathrm{put}\:\:\mathrm{descending}\:\mathrm{value}\:\mathrm{of}\:\mathrm{r}\:\mathrm{in} \\ $$$$\:\mathrm{terms}\:\mathrm{of}\:\mathrm{power}\:\mathrm{series}\: \\ $$$$\:\:\:\mathrm{y}=\:\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}} \:=\:\mathrm{a}_{\mathrm{0}} +\mathrm{ax}+\mathrm{a}_{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +…. \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\: \\ $$$$ \\ $$$$\: \\ $$$$\:\:\: \\ $$
