1-x-2-dx-x-4-

Question Number 107036 by john santu last updated on 08/Aug/20

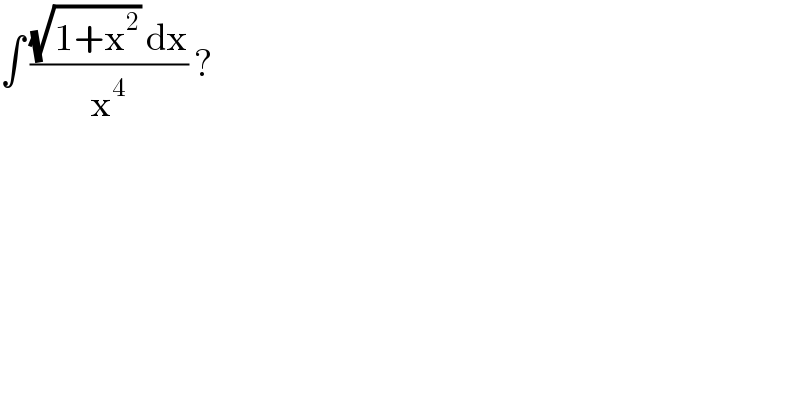
$$\int\:\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} }\:? \\ $$

Commented by kaivan.ahmadi last updated on 08/Aug/20

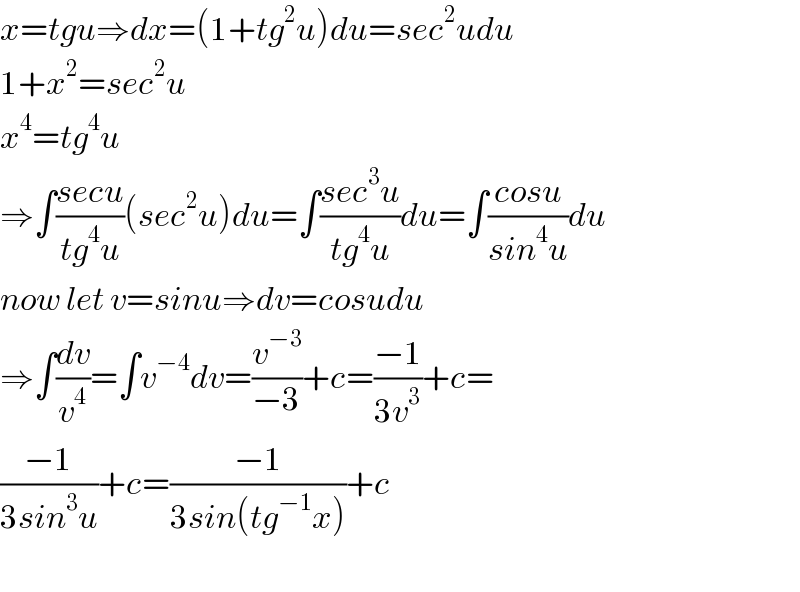
x=tgu⇒dx=(1+tg^2 u)du=sec^2 udu 1+x^2 =sec^2 u x^4 =tg^4 u ⇒∫((secu)/(tg^4 u))(sec^2 u)du=∫((sec^3 u)/(tg^4 u))du=∫((cosu)/(sin^4 u))du now let v=sinu⇒dv=cosudu ⇒∫(dv/v^4 )=∫v^(−4) dv=(v^(−3) /(−3))+c=((−1)/(3v^3 ))+c= ((−1)/(3sin^3 u))+c=((−1)/(3sin(tg^(−1) x)))+c

$${x}={tgu}\Rightarrow{dx}=\left(\mathrm{1}+{tg}^{\mathrm{2}} {u}\right){du}={sec}^{\mathrm{2}} {udu} \\ $$$$\mathrm{1}+{x}^{\mathrm{2}} ={sec}^{\mathrm{2}} {u} \\ $$$${x}^{\mathrm{4}} ={tg}^{\mathrm{4}} {u} \\ $$$$\Rightarrow\int\frac{{secu}}{{tg}^{\mathrm{4}} {u}}\left({sec}^{\mathrm{2}} {u}\right){du}=\int\frac{{sec}^{\mathrm{3}} {u}}{{tg}^{\mathrm{4}} {u}}{du}=\int\frac{{cosu}}{{sin}^{\mathrm{4}} {u}}{du} \\ $$$${now}\:{let}\:{v}={sinu}\Rightarrow{dv}={cosudu} \\ $$$$\Rightarrow\int\frac{{dv}}{{v}^{\mathrm{4}} }=\int{v}^{−\mathrm{4}} {dv}=\frac{{v}^{−\mathrm{3}} }{−\mathrm{3}}+{c}=\frac{−\mathrm{1}}{\mathrm{3}{v}^{\mathrm{3}} }+{c}= \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}{sin}^{\mathrm{3}} {u}}+{c}=\frac{−\mathrm{1}}{\mathrm{3}{sin}\left({tg}^{−\mathrm{1}} {x}\right)}+{c} \\ $$$$ \\ $$

Answered by Dwaipayan Shikari last updated on 08/Aug/20

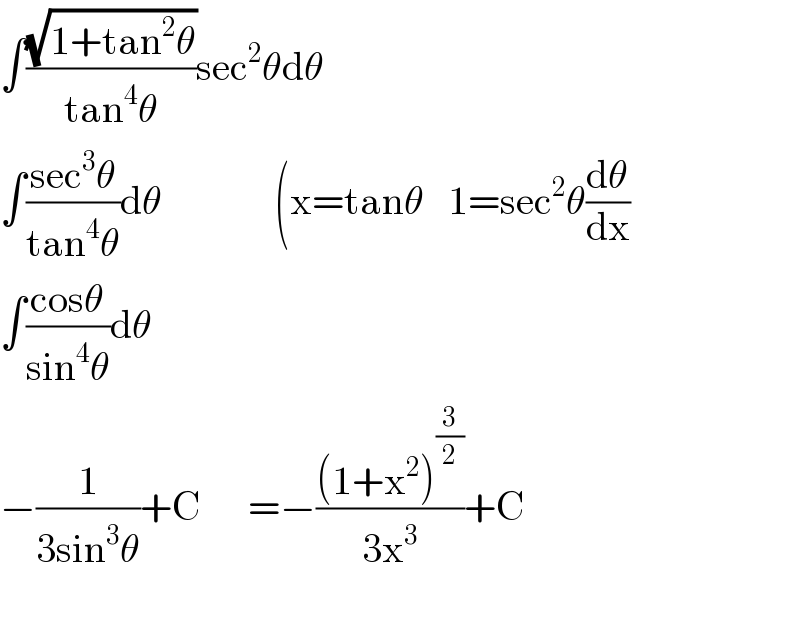
∫((√(1+tan^2 θ))/(tan^4 θ))sec^2 θdθ ∫((sec^3 θ)/(tan^4 θ))dθ (x=tanθ 1=sec^2 θ(dθ/dx) ∫((cosθ)/(sin^4 θ))dθ −(1/(3sin^3 θ))+C =−(((1+x^2 )^(3/2) )/(3x^3 ))+C

$$\int\frac{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}}{\mathrm{tan}^{\mathrm{4}} \theta}\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\int\frac{\mathrm{sec}^{\mathrm{3}} \theta}{\mathrm{tan}^{\mathrm{4}} \theta}\mathrm{d}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}=\mathrm{tan}\theta\:\:\:\mathrm{1}=\mathrm{sec}^{\mathrm{2}} \theta\frac{\mathrm{d}\theta}{\mathrm{dx}}\right. \\ $$$$\int\frac{\mathrm{cos}\theta}{\mathrm{sin}^{\mathrm{4}} \theta}\mathrm{d}\theta \\ $$$$−\frac{\mathrm{1}}{\mathrm{3sin}^{\mathrm{3}} \theta}+\mathrm{C}\:\:\:\:\:\:=−\frac{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3x}^{\mathrm{3}} }+\mathrm{C} \\ $$$$ \\ $$

Answered by bobhans last updated on 08/Aug/20

^� bobhans^� ∫ ((√(x^2 (1+(1/x^2 ))))/x^4 ) dx= ∫ ((x(√(1+(1/x^2 ))) dx)/x^4 ) =∫ ((√(1+(1/x^2 )))/x^3 ) dx . [ let u = 1+(1/x^2 ) ] du = −2x^(−3) dx ⇒ (dx/x^3 ) = −(du/2) −∫ (u^(1/2) /2) du = −(1/2)×(2/3)u^(3/2) +c −(1/3)(√((1+(1/x^2 ))^3 ))+c = −((x^2 +1)/(3x^2 ))×((√(x^2 +1))/x)+c =−(((x^2 +1)(√(x^2 +1)))/(3x^3 )) + c

$$\:\:\:\:\:\:\hat {\:}\mathrm{bobhan}\hat {\mathrm{s}} \\ $$$$\int\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}}{\mathrm{x}^{\mathrm{4}} }\:\:\mathrm{dx}=\:\int\:\frac{\mathrm{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\int\:\frac{\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}{\mathrm{x}^{\mathrm{3}} }\:\mathrm{dx}\:.\:\left[\:\mathrm{let}\:\mathrm{u}\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\right]\: \\ $$$$\mathrm{du}\:=\:−\mathrm{2x}^{−\mathrm{3}} \:\mathrm{dx}\:\Rightarrow\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} }\:=\:−\frac{\mathrm{du}}{\mathrm{2}} \\ $$$$−\int\:\frac{\mathrm{u}^{\mathrm{1}/\mathrm{2}} }{\mathrm{2}}\:\mathrm{du}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}\mathrm{u}^{\mathrm{3}/\mathrm{2}} \:+\mathrm{c}\: \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{3}} }+\mathrm{c}\:=\:−\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{3x}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{x}}+\mathrm{c} \\ $$$$=−\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{3x}^{\mathrm{3}} }\:+\:\mathrm{c} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply