Question Number 92860 by i jagooll last updated on 09/May/20
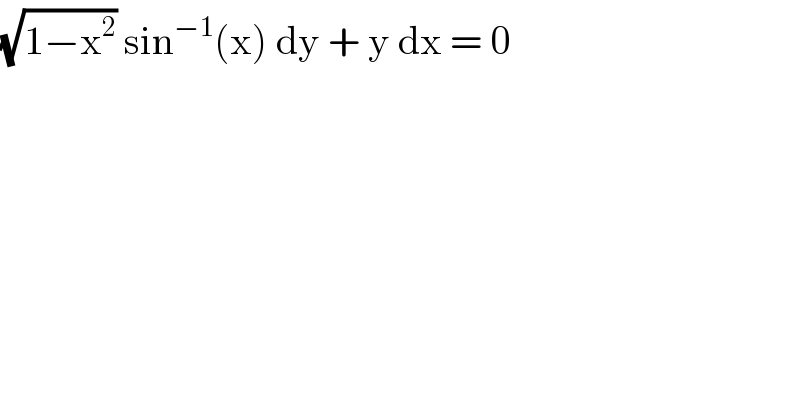
$$\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\:\mathrm{dy}\:+\:\mathrm{y}\:\mathrm{dx}\:=\:\mathrm{0}\: \\ $$
Commented by john santu last updated on 09/May/20
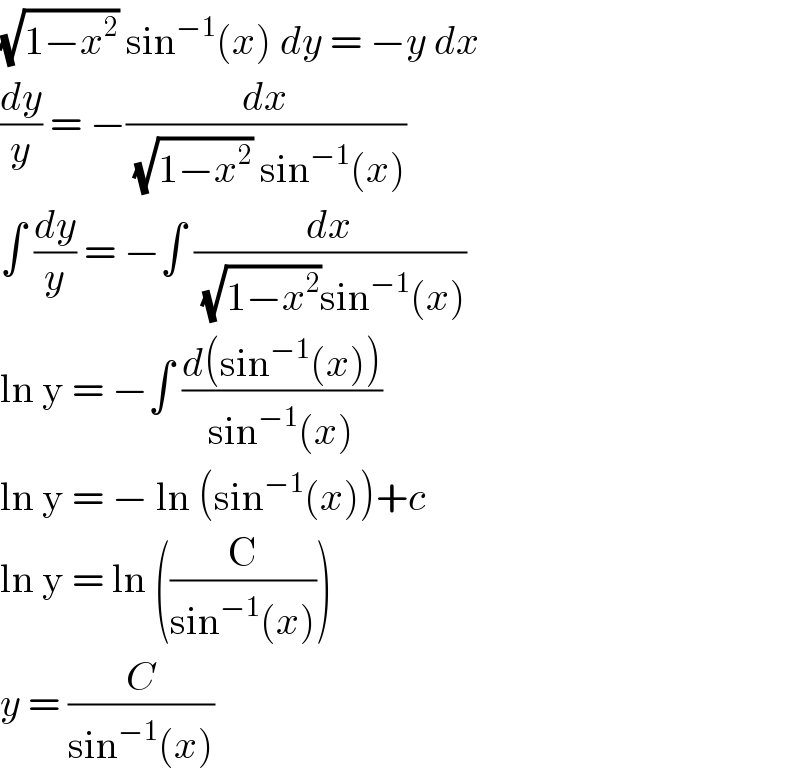
$$\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\:{dy}\:=\:−{y}\:{dx} \\ $$$$\frac{{dy}}{{y}}\:=\:−\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\mathrm{sin}^{−\mathrm{1}} \left({x}\right)} \\ $$$$\int\:\frac{{dy}}{{y}}\:=\:−\int\:\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\mathrm{sin}^{−\mathrm{1}} \left({x}\right)} \\ $$$$\mathrm{ln}\:\mathrm{y}\:=\:−\int\:\frac{{d}\left(\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\right)}{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)} \\ $$$$\mathrm{ln}\:\mathrm{y}\:=\:−\:\mathrm{ln}\:\left(\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\right)+{c} \\ $$$$\mathrm{ln}\:\mathrm{y}\:=\:\mathrm{ln}\:\left(\frac{\mathrm{C}}{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}\right)\: \\ $$$${y}\:=\:\frac{{C}}{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}\: \\ $$
Commented by niroj last updated on 09/May/20
����
