Menu Close

1-x-2-x-1-2-x-2-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 125194 by bemath last updated on 09/Dec/20
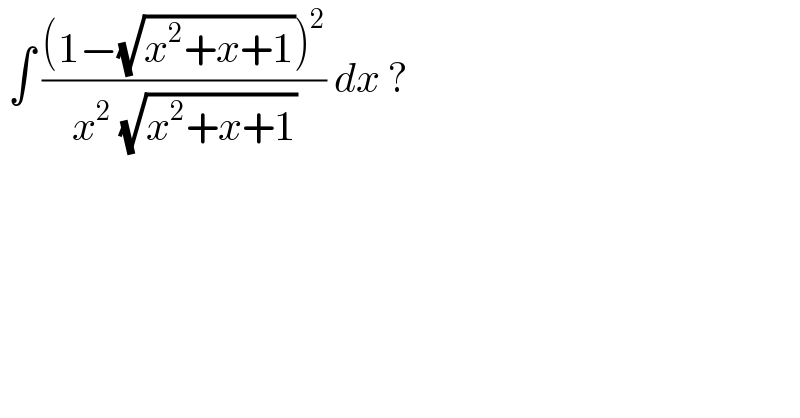
∫ (((1−(√(x^2 +x+1)))^2 )/(x^2 (√(x^2 +x+1)))) dx ?
∫(1−x2+x+1)2x2x2+x+1dx?
Answered by liberty last updated on 09/Dec/20
by second Euler substitution we set (√(x^2 +x+1)) = xt + 1 ; then x^2 +x+1 = x^2 t^2 + 2xt + 1 ; x=((2t−1)/(1−t^2 )) dx = ((2t^2 −2t+2)/((1−t^2 )^2 )) dt ; I= ∫(((1−(√(x^2 +x+1)) )^2 )/(x^2 (√(x^2 +x+1)))) dx = 2∫ (t^2 /(1−t^2 )) dt I = −2t + ln ∣ ((1+t)/(1−t)) ∣ + c I = −((2((√(x^2 +x+1)) −1))/x) + ln ∣ ((x+(√(x^2 +x+1))−1)/(x−(√(x^2 +x+1)) +1)) ∣ + c = −((2((√(x^2 +x+1)) −1))/x) + ln ∣2x+2(√(x^2 +x+1)) +1 ∣ + c
bysecondEulersubstitutionwesetx2+x+1=xt+1;thenx2+x+1=x2t2+2xt+1;x=2t−11−t2dx=2t2−2t+2(1−t2)2dt;I=∫(1−x2+x+1)2x2x2+x+1dx=2∫t21−t2dtI=−2t+ln∣1+t1−t∣+cI=−2(x2+x+1−1)x+ln∣x+x2+x+1−1x−x2+x+1+1∣+c=−2(x2+x+1−1)x+ln∣2x+2x2+x+1+1∣+c

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *