Question Number 156931 by cortano last updated on 17/Oct/21
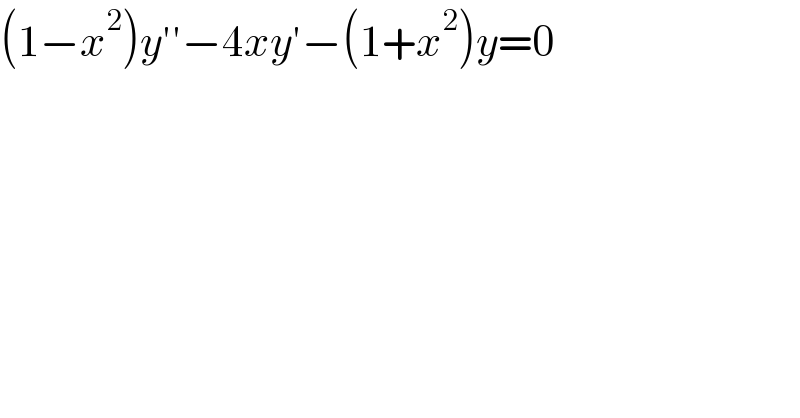
$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}''−\mathrm{4}{xy}'−\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}=\mathrm{0} \\ $$
Commented by john_santu last updated on 17/Oct/21

$${y}=\frac{\mathrm{sin}\:{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:+\:{c} \\ $$
Commented by aliyn last updated on 18/Oct/21

$$ \\ $$$$\boldsymbol{{Solution}}: \\ $$$$ \\ $$$$\boldsymbol{{y}}^{'} \:=\:\frac{\mathrm{4}\boldsymbol{{x}}\:\pm\:\sqrt{\mathrm{16}\boldsymbol{{x}}^{\mathrm{2}} \:+\mathrm{4}\:+\:\mathrm{4}\:\boldsymbol{{x}}^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\boldsymbol{{y}}^{'} \:=\:\frac{\mathrm{2}\boldsymbol{{x}}\:\pm\:\sqrt{\mathrm{5}\boldsymbol{{x}}^{\mathrm{2}} \:+\:\mathrm{1}}}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} } \\ $$$$ \\ $$$$\boldsymbol{{dy}}\:=\:\frac{\mathrm{2}\boldsymbol{{x}}\:}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\:\pm\:\frac{\sqrt{\mathrm{5}\boldsymbol{{x}}^{\mathrm{2}} \:+\:\mathrm{1}}}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\boldsymbol{{y}}\:=\:\:\boldsymbol{{ln}}\:\mid\:\frac{\mathrm{1}}{\:\sqrt{\:\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}\:\mid\:\pm\:\int\:\:\frac{\sqrt{\mathrm{5}\boldsymbol{{x}}^{\mathrm{2}} \:+\:\mathrm{1}}}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\boldsymbol{{now}}\::\:\boldsymbol{{x}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\boldsymbol{{tany}}\:\rightarrow\:\boldsymbol{{dx}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\boldsymbol{{sec}}^{\mathrm{2}} \boldsymbol{{y}}\:\boldsymbol{{dy}} \\ $$$$ \\ $$$$\boldsymbol{{complete}} \\ $$
Answered by mindispower last updated on 17/Oct/21
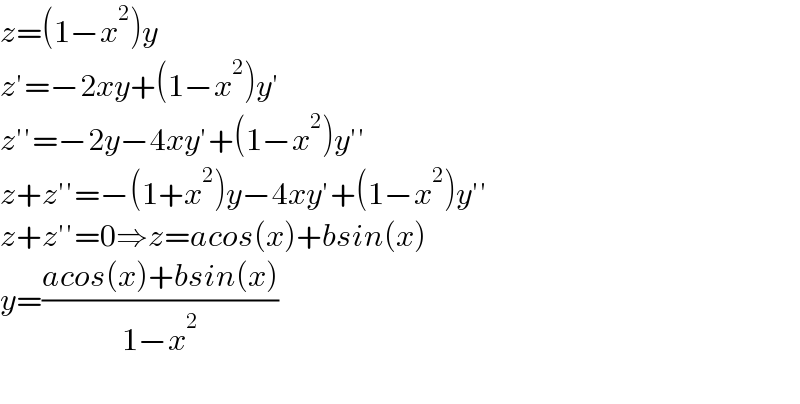
$${z}=\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y} \\ $$$${z}'=−\mathrm{2}{xy}+\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}' \\ $$$${z}''=−\mathrm{2}{y}−\mathrm{4}{xy}'+\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}'' \\ $$$${z}+{z}''=−\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}−\mathrm{4}{xy}'+\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}'' \\ $$$${z}+{z}''=\mathrm{0}\Rightarrow{z}={acos}\left({x}\right)+{bsin}\left({x}\right) \\ $$$${y}=\frac{{acos}\left({x}\right)+{bsin}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$ \\ $$
