Question Number 49220 by malwaan last updated on 04/Dec/18
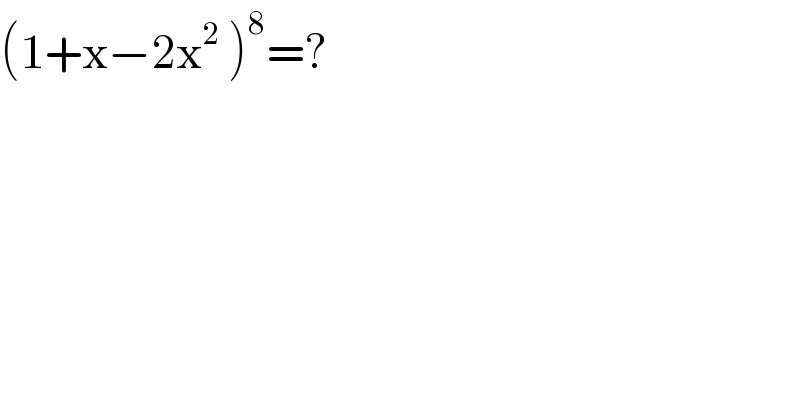
$$\left(\mathrm{1}+\mathrm{x}−\mathrm{2x}^{\mathrm{2}} \:\right)^{\mathrm{8}} =? \\ $$
Commented by Abdo msup. last updated on 04/Dec/18
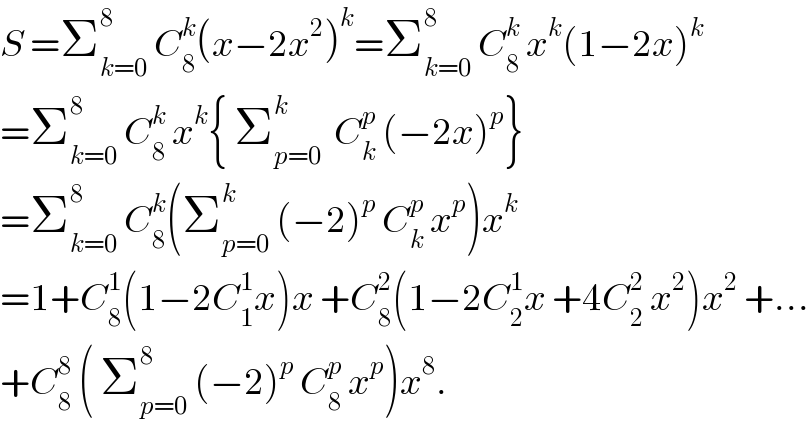
$${S}\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{8}} \:{C}_{\mathrm{8}} ^{{k}} \left({x}−\mathrm{2}{x}^{\mathrm{2}} \right)^{{k}} =\sum_{{k}=\mathrm{0}} ^{\mathrm{8}} \:{C}_{\mathrm{8}} ^{{k}} \:{x}^{{k}} \left(\mathrm{1}−\mathrm{2}{x}\right)^{{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{8}} \:{C}_{\mathrm{8}} ^{{k}} \:{x}^{{k}} \left\{\:\sum_{{p}=\mathrm{0}} ^{{k}} \:\:{C}_{{k}} ^{{p}} \:\left(−\mathrm{2}{x}\right)^{{p}} \right\} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{8}} \:{C}_{\mathrm{8}} ^{{k}} \left(\sum_{{p}=\mathrm{0}} ^{{k}} \:\left(−\mathrm{2}\right)^{{p}} \:{C}_{{k}} ^{{p}} \:{x}^{{p}} \right){x}^{{k}} \\ $$$$=\mathrm{1}+{C}_{\mathrm{8}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{2}{C}_{\mathrm{1}} ^{\mathrm{1}} {x}\right){x}\:+{C}_{\mathrm{8}} ^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{C}_{\mathrm{2}} ^{\mathrm{1}} {x}\:+\mathrm{4}{C}_{\mathrm{2}} ^{\mathrm{2}} \:{x}^{\mathrm{2}} \right){x}^{\mathrm{2}} \:+… \\ $$$$+{C}_{\mathrm{8}} ^{\mathrm{8}} \:\left(\:\sum_{{p}=\mathrm{0}} ^{\mathrm{8}} \:\left(−\mathrm{2}\right)^{{p}} \:{C}_{\mathrm{8}} ^{{p}} \:{x}^{{p}} \right){x}^{\mathrm{8}} . \\ $$
Commented by malwaan last updated on 05/Dec/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
