Question Number 109912 by mohammad17 last updated on 26/Aug/20
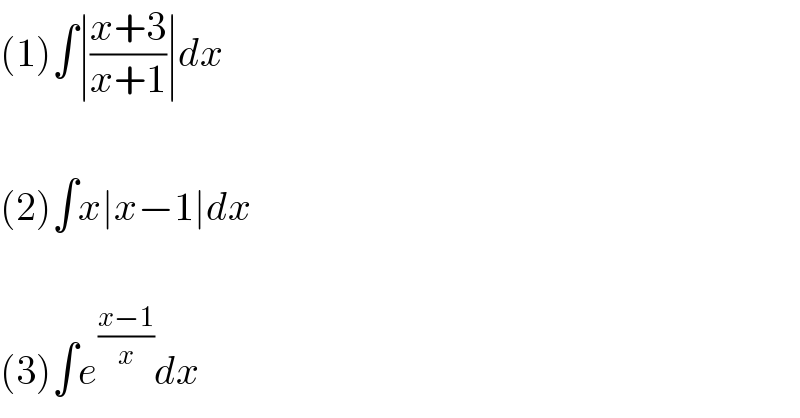
$$\left(\mathrm{1}\right)\int\mid\frac{{x}+\mathrm{3}}{{x}+\mathrm{1}}\mid{dx} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\int{x}\mid{x}−\mathrm{1}\mid{dx} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\int{e}^{\frac{{x}−\mathrm{1}}{{x}}} {dx} \\ $$
Commented by mohammad17 last updated on 26/Aug/20
$$ \\ $$$${ho}\:{is}\:{can}\:{help}\:{me} \\ $$
Answered by mathmax by abdo last updated on 26/Aug/20
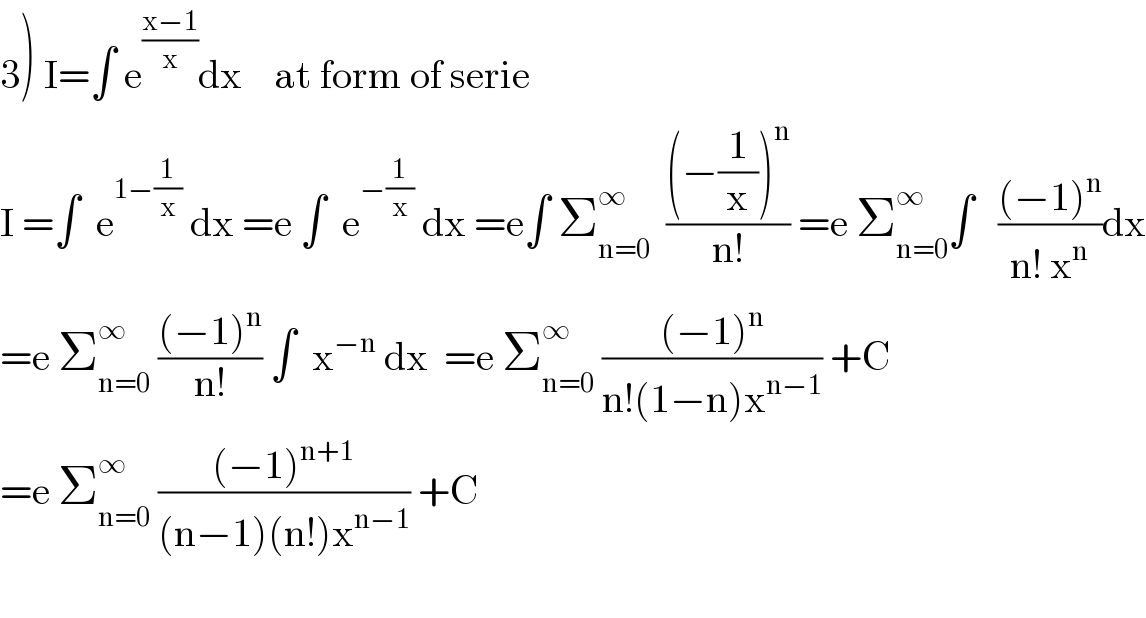
$$\left.\mathrm{3}\right)\:\mathrm{I}=\int\:\mathrm{e}^{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}} \mathrm{dx}\:\:\:\:\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie} \\ $$$$\mathrm{I}\:=\int\:\:\mathrm{e}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}} \:\mathrm{dx}\:=\mathrm{e}\:\int\:\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \:\mathrm{dx}\:=\mathrm{e}\int\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{n}} }{\mathrm{n}!}\:=\mathrm{e}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \int\:\:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!\:\mathrm{x}^{\mathrm{n}} }\mathrm{dx} \\ $$$$=\mathrm{e}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!}\:\int\:\:\mathrm{x}^{−\mathrm{n}} \:\mathrm{dx}\:\:=\mathrm{e}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!\left(\mathrm{1}−\mathrm{n}\right)\mathrm{x}^{\mathrm{n}−\mathrm{1}} }\:+\mathrm{C} \\ $$$$=\mathrm{e}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}!\right)\mathrm{x}^{\mathrm{n}−\mathrm{1}} }\:+\mathrm{C} \\ $$$$ \\ $$
Commented by mohammad17 last updated on 26/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 26/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mathmax by abdo last updated on 26/Aug/20
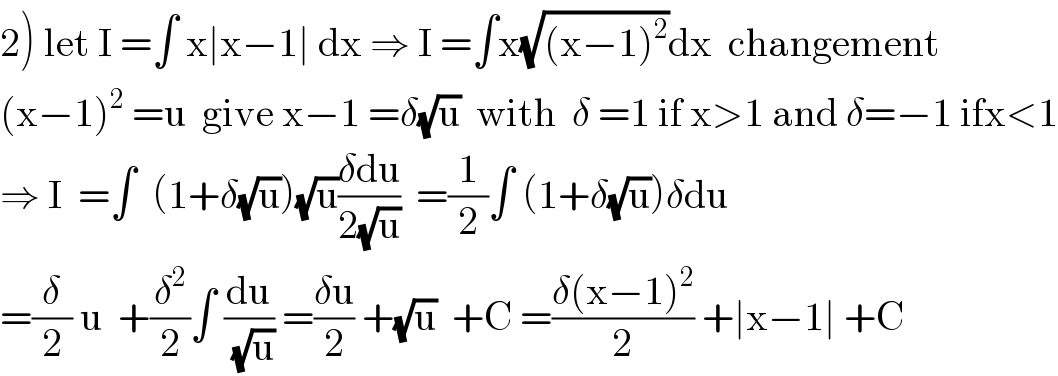
$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{I}\:=\int\:\mathrm{x}\mid\mathrm{x}−\mathrm{1}\mid\:\mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int\mathrm{x}\sqrt{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{changement} \\ $$$$\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:=\mathrm{u}\:\:\mathrm{give}\:\mathrm{x}−\mathrm{1}\:=\delta\sqrt{\mathrm{u}}\:\:\mathrm{with}\:\:\delta\:=\mathrm{1}\:\mathrm{if}\:\mathrm{x}>\mathrm{1}\:\mathrm{and}\:\delta=−\mathrm{1}\:\mathrm{ifx}<\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{I}\:\:=\int\:\:\left(\mathrm{1}+\delta\sqrt{\mathrm{u}}\right)\sqrt{\mathrm{u}}\frac{\delta\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{u}}}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{1}+\delta\sqrt{\mathrm{u}}\right)\delta\mathrm{du} \\ $$$$=\frac{\delta}{\mathrm{2}}\:\mathrm{u}\:\:+\frac{\delta^{\mathrm{2}} }{\mathrm{2}}\int\:\frac{\mathrm{du}}{\:\sqrt{\mathrm{u}}}\:=\frac{\delta\mathrm{u}}{\mathrm{2}}\:+\sqrt{\mathrm{u}}\:\:+\mathrm{C}\:=\frac{\delta\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\mid\mathrm{x}−\mathrm{1}\mid\:+\mathrm{C} \\ $$
Commented by mohammad17 last updated on 26/Aug/20

$${thank}\:{you}\:{sir} \\ $$
