Menu Close

1-x-4-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 36649 by rahul 19 last updated on 03/Jun/18
∫ (1/(x^4 +1)) dx
$$\int\:\frac{\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{1}}\:{dx} \\ $$
Commented by rahul 19 last updated on 03/Jun/18
∫ ((1/x^2 )/(x^2 +(1/x^2 ))) dx ⇒∫ ((1+(1/x^2 )−1)/(x^2 +(1/x^2 ))) dx ⇒∫ ((1+(1/x^2 ))/((x−(1/x))^2 +2))dx − ∫ (1/((x−(1/x))^2 +2))dx Continue....
$$\int\:\frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:{dx}\: \\ $$$$\Rightarrow\int\:\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:{dx} \\ $$$$\Rightarrow\int\:\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}{dx}\:−\:\int\:\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}{dx} \\ $$$$\mathrm{Continue}…. \\ $$
Commented by rahul 19 last updated on 03/Jun/18
By doing this way i am getting wrong result ! Can someone continue from here and do check?
$$\mathrm{By}\:\mathrm{doing}\:\mathrm{this}\:\mathrm{way}\:\mathrm{i}\:\mathrm{am}\:\mathrm{getting}\:\mathrm{wrong} \\ $$$$\mathrm{result}\:!\:\mathrm{Can}\:\mathrm{someone}\:\mathrm{continue}\:\mathrm{from} \\ $$$$\mathrm{here}\:\mathrm{and}\:\mathrm{do}\:\mathrm{check}? \\ $$
Commented by abdo mathsup last updated on 03/Jun/18
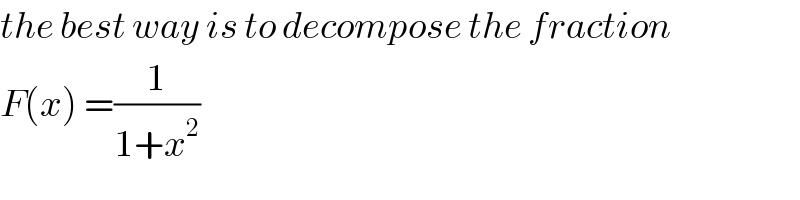
the best way is to decompose the fraction F(x) =(1/(1+x^2 ))
$${the}\:{best}\:{way}\:{is}\:{to}\:{decompose}\:{the}\:{fraction} \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$
Commented by abdo mathsup last updated on 04/Jun/18
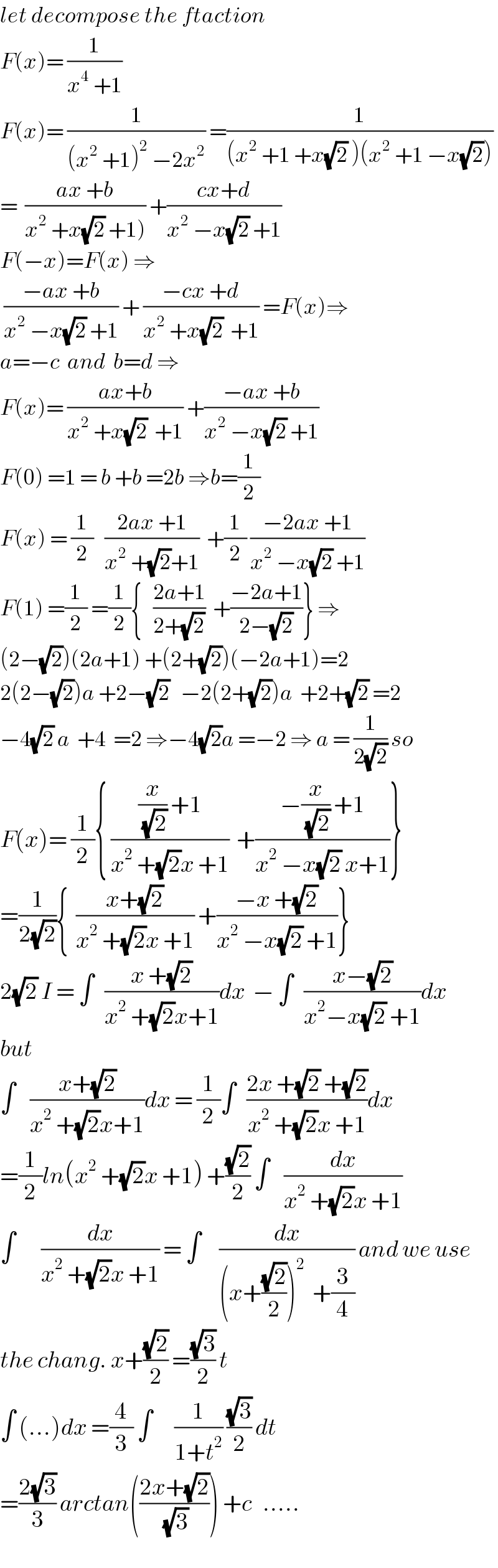
let decompose the ftaction F(x)= (1/(x^4 +1)) F(x)= (1/((x^2 +1)^2 −2x^2 )) =(1/((x^2 +1 +x(√2) )(x^2 +1 −x(√2)))) = ((ax +b)/(x^2 +x(√2) +1))) +((cx+d)/(x^2 −x(√2) +1)) F(−x)=F(x) ⇒ ((−ax +b)/(x^2 −x(√2) +1)) + ((−cx +d)/(x^2 +x(√2) +1)) =F(x)⇒ a=−c and b=d ⇒ F(x)= ((ax+b)/(x^2 +x(√2) +1)) +((−ax +b)/(x^2 −x(√2) +1)) F(0) =1 = b +b =2b ⇒b=(1/2) F(x) = (1/2) ((2ax +1)/(x^2 +(√2)+1)) +(1/2) ((−2ax +1)/(x^2 −x(√2) +1)) F(1) =(1/2) =(1/2){ ((2a+1)/(2+(√2))) +((−2a+1)/(2−(√2)))} ⇒ (2−(√2))(2a+1) +(2+(√2))(−2a+1)=2 2(2−(√2))a +2−(√2) −2(2+(√2))a +2+(√2) =2 −4(√2) a +4 =2 ⇒−4(√2)a =−2 ⇒ a = (1/(2(√2))) so F(x)= (1/2){ (((x/( (√2))) +1)/(x^2 +(√2)x +1)) +((−(x/( (√2))) +1)/(x^2 −x(√2) x+1))} =(1/(2(√2))){ ((x+(√2))/(x^2 +(√2)x +1)) +((−x +(√2))/(x^2 −x(√2) +1))} 2(√2) I = ∫ ((x +(√2))/(x^2 +(√2)x+1))dx − ∫ ((x−(√2))/(x^2 −x(√2) +1))dx but ∫ ((x+(√2))/(x^2 +(√2)x+1))dx = (1/2)∫ ((2x +(√2) +(√2))/(x^2 +(√2)x +1))dx =(1/2)ln(x^2 +(√2)x +1) +((√2)/2) ∫ (dx/(x^2 +(√2)x +1)) ∫ (dx/(x^2 +(√2)x +1)) = ∫ (dx/((x+((√2)/2))^2 +(3/4))) and we use the chang. x+((√2)/2) =((√3)/2) t ∫ (...)dx =(4/3) ∫ (1/(1+t^2 )) ((√3)/2) dt =((2(√3))/3) arctan(((2x+(√2))/( (√3)))) +c .....
$${let}\:{decompose}\:{the}\:{ftaction} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{{x}^{\mathrm{4}} \:+\mathrm{1}} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{2}{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\:+{x}\sqrt{\mathrm{2}}\:\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\:−{x}\sqrt{\mathrm{2}}\right)} \\ $$$$=\:\:\frac{{ax}\:+{b}}{\left.{x}^{\mathrm{2}} \:+{x}\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:−{x}\sqrt{\mathrm{2}}\:+\mathrm{1}} \\ $$$${F}\left(−{x}\right)={F}\left({x}\right)\:\Rightarrow \\ $$$$\:\frac{−{ax}\:+{b}}{{x}^{\mathrm{2}} \:−{x}\sqrt{\mathrm{2}}\:+\mathrm{1}}\:+\:\frac{−{cx}\:+{d}}{{x}^{\mathrm{2}} \:+{x}\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\:={F}\left({x}\right)\Rightarrow \\ $$$${a}=−{c}\:\:{and}\:\:{b}={d}\:\Rightarrow\: \\ $$$${F}\left({x}\right)=\:\frac{{ax}+{b}}{{x}^{\mathrm{2}} \:+{x}\sqrt{\mathrm{2}}\:\:+\mathrm{1}}\:+\frac{−{ax}\:+{b}}{{x}^{\mathrm{2}} \:−{x}\sqrt{\mathrm{2}}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\:{b}\:+{b}\:=\mathrm{2}{b}\:\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\frac{\mathrm{2}{ax}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}+\mathrm{1}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\frac{−\mathrm{2}{ax}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:−{x}\sqrt{\mathrm{2}}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\:\frac{\mathrm{2}{a}+\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:\:+\frac{−\mathrm{2}{a}+\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{2}}}\right\}\:\Rightarrow \\ $$$$\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{2}{a}+\mathrm{1}\right)\:+\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left(−\mathrm{2}{a}+\mathrm{1}\right)=\mathrm{2} \\ $$$$\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){a}\:+\mathrm{2}−\sqrt{\mathrm{2}}\:\:\:−\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){a}\:\:+\mathrm{2}+\sqrt{\mathrm{2}}\:=\mathrm{2} \\ $$$$−\mathrm{4}\sqrt{\mathrm{2}}\:{a}\:\:+\mathrm{4}\:\:=\mathrm{2}\:\Rightarrow−\mathrm{4}\sqrt{\mathrm{2}}{a}\:=−\mathrm{2}\:\Rightarrow\:{a}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:{so} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\frac{{x}}{\:\sqrt{\mathrm{2}}}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}\:\:+\frac{−\frac{{x}}{\:\sqrt{\mathrm{2}}}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:−{x}\sqrt{\mathrm{2}}\:{x}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\:\frac{{x}+\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}\:+\frac{−{x}\:+\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} \:−{x}\sqrt{\mathrm{2}}\:+\mathrm{1}}\right\} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}}\:{I}\:=\:\int\:\:\:\frac{{x}\:+\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}+\mathrm{1}}{dx}\:\:−\:\int\:\:\:\frac{{x}−\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} −{x}\sqrt{\mathrm{2}}\:+\mathrm{1}}{dx} \\ $$$${but} \\ $$$$\int\:\:\:\:\frac{{x}+\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}+\mathrm{1}}{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{\mathrm{2}{x}\:+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}} \\ $$$$\int\:\:\:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}\:=\:\int\:\:\:\:\:\frac{{dx}}{\left({x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:+\frac{\mathrm{3}}{\mathrm{4}}}\:{and}\:{we}\:{use} \\ $$$${the}\:{chang}.\:{x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{t} \\ $$$$\int\:\left(…\right){dx}\:=\frac{\mathrm{4}}{\mathrm{3}}\:\int\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{dt} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{2}{x}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right)\:+{c}\:\:\:….. \\ $$
Answered by ajfour last updated on 03/Jun/18
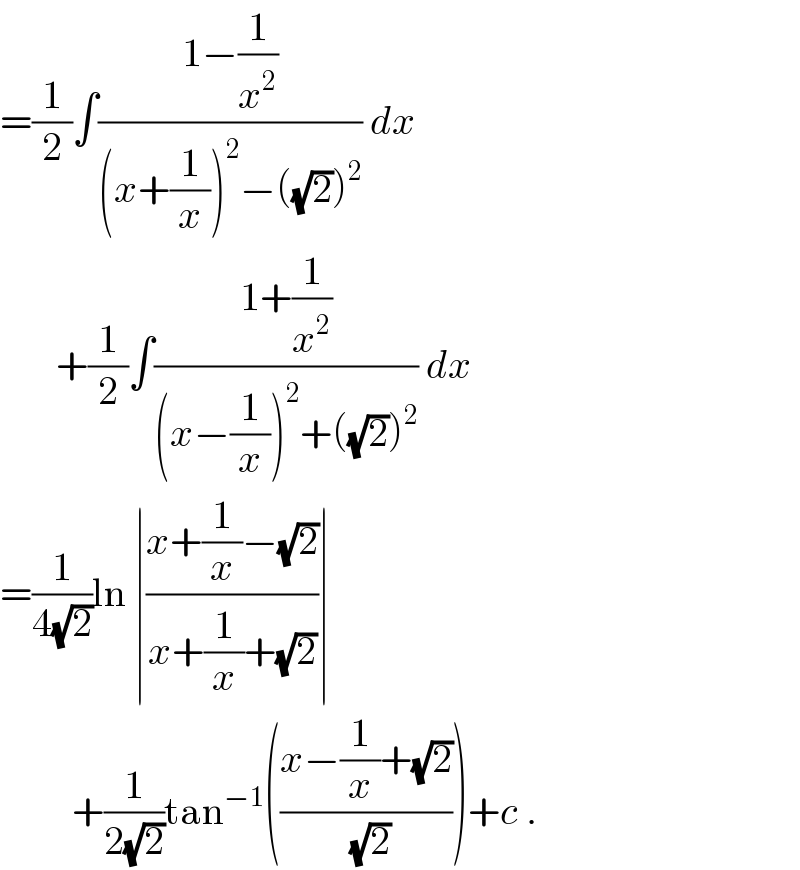
=(1/2)∫((1−(1/x^2 ))/((x+(1/x))^2 −((√2))^2 )) dx +(1/2)∫((1+(1/x^2 ))/((x−(1/x))^2 +((√2))^2 )) dx =(1/(4(√2)))ln ∣((x+(1/x)−(√2))/(x+(1/x)+(√2)))∣ +(1/(2(√2)))tan^(−1) (((x−(1/x)+(√2))/( (√2))))+c .
$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\frac{{x}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}\mid \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\right)+{c}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *