Menu Close

1-x-4-1-x-2-dx-2-3-5-x-3-dx-3-0-pi-2-4-sin-x-dx-4-e-2x-2-5x-3-dx-5-x-3-y-2x-2-y-2xy-8y-0-6-x-4-y-4-dx-2x-3-y-dy-0-7-2-xy-y-

Tinku Tara 0 Comments
Pin




Question Number 108893 by bobhans last updated on 20/Aug/20
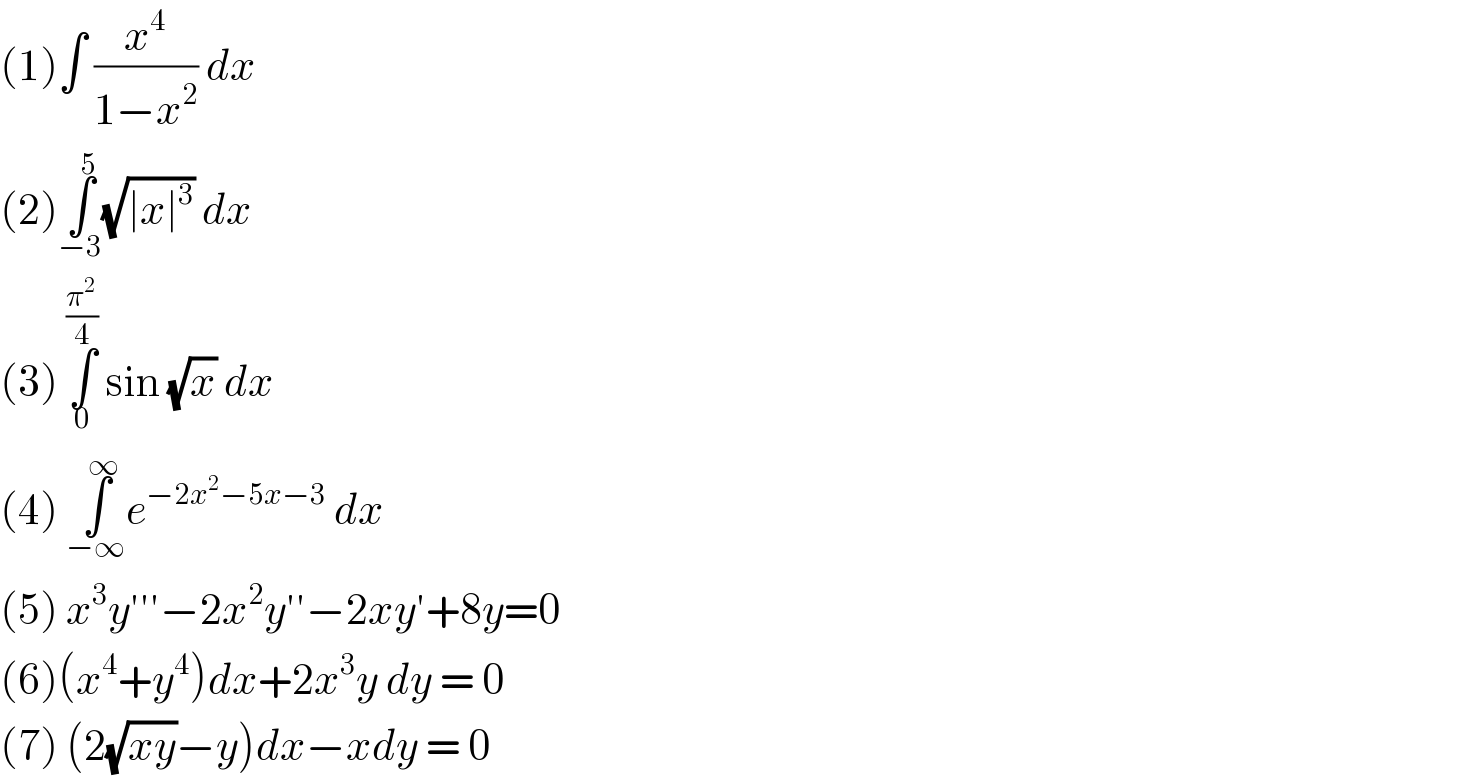
(1)∫ (x^4 /(1−x^2 )) dx (2)∫_(−3) ^5 (√(∣x∣^3 )) dx (3) ∫_0 ^(π^2 /4) sin (√x) dx (4) ∫_(−∞) ^∞ e^(−2x^2 −5x−3) dx (5) x^3 y′′′−2x^2 y′′−2xy′+8y=0 (6)(x^4 +y^4 )dx+2x^3 y dy = 0 (7) (2(√(xy))−y)dx−xdy = 0
$$\left(\mathrm{1}\right)\int\:\frac{{x}^{\mathrm{4}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\: \\ $$$$\left(\mathrm{2}\right)\underset{−\mathrm{3}} {\overset{\mathrm{5}} {\int}}\sqrt{\mid{x}\mid^{\mathrm{3}} }\:{dx}\: \\ $$$$\left(\mathrm{3}\right)\:\underset{\mathrm{0}} {\overset{\frac{\pi^{\mathrm{2}} }{\mathrm{4}}} {\int}}\:\mathrm{sin}\:\sqrt{{x}}\:{dx}\: \\ $$$$\left(\mathrm{4}\right)\:\underset{−\infty} {\overset{\infty} {\int}}{e}^{−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3}} \:{dx}\: \\ $$$$\left(\mathrm{5}\right)\:{x}^{\mathrm{3}} {y}'''−\mathrm{2}{x}^{\mathrm{2}} {y}''−\mathrm{2}{xy}'+\mathrm{8}{y}=\mathrm{0} \\ $$$$\left(\mathrm{6}\right)\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} \right){dx}+\mathrm{2}{x}^{\mathrm{3}} {y}\:{dy}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{7}\right)\:\left(\mathrm{2}\sqrt{{xy}}−{y}\right){dx}−{xdy}\:=\:\mathrm{0} \\ $$
Answered by bemath last updated on 20/Aug/20
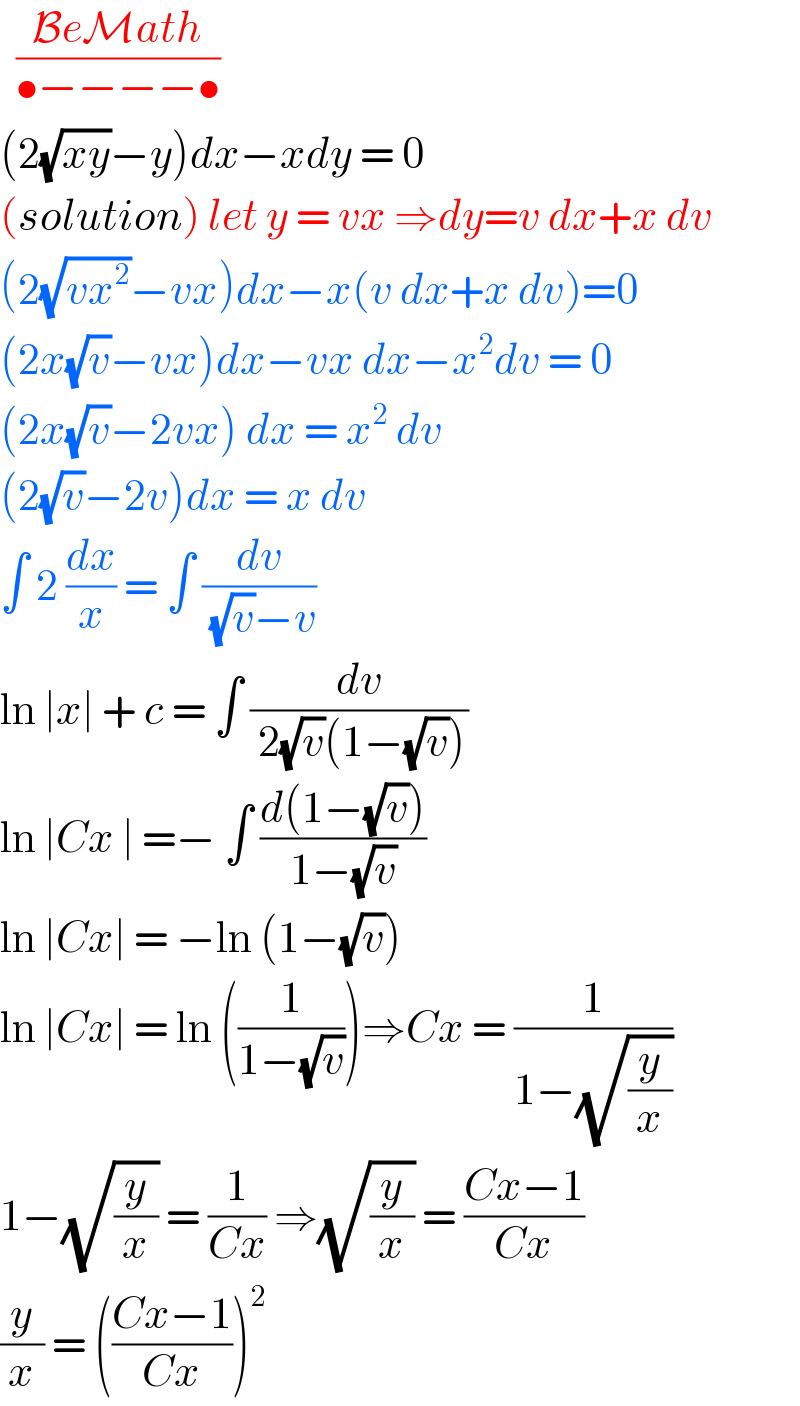
((BeMath)/(•−−−−•)) (2(√(xy))−y)dx−xdy = 0 (solution) let y = vx ⇒dy=v dx+x dv (2(√(vx^2 ))−vx)dx−x(v dx+x dv)=0 (2x(√v)−vx)dx−vx dx−x^2 dv = 0 (2x(√v)−2vx) dx = x^2 dv (2(√v)−2v)dx = x dv ∫ 2 (dx/x) = ∫ (dv/( (√v)−v)) ln ∣x∣ + c = ∫ (dv/( 2(√v)(1−(√v)))) ln ∣Cx ∣ =− ∫ ((d(1−(√v)))/(1−(√v))) ln ∣Cx∣ = −ln (1−(√v)) ln ∣Cx∣ = ln ((1/(1−(√v))))⇒Cx = (1/(1−(√(y/x)))) 1−(√(y/x)) = (1/(Cx)) ⇒(√(y/x)) = ((Cx−1)/(Cx)) (y/x) = (((Cx−1)/(Cx)))^2
$$\:\:\frac{\mathcal{B}{e}\mathcal{M}{ath}}{\bullet−−−−\bullet} \\ $$$$\left(\mathrm{2}\sqrt{{xy}}−{y}\right){dx}−{xdy}\:=\:\mathrm{0} \\ $$$$\left({solution}\right)\:{let}\:{y}\:=\:{vx}\:\Rightarrow{dy}={v}\:{dx}+{x}\:{dv} \\ $$$$\left(\mathrm{2}\sqrt{{vx}^{\mathrm{2}} }−{vx}\right){dx}−{x}\left({v}\:{dx}+{x}\:{dv}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}\sqrt{{v}}−{vx}\right){dx}−{vx}\:{dx}−{x}^{\mathrm{2}} {dv}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}{x}\sqrt{{v}}−\mathrm{2}{vx}\right)\:{dx}\:=\:{x}^{\mathrm{2}} \:{dv}\: \\ $$$$\left(\mathrm{2}\sqrt{{v}}−\mathrm{2}{v}\right){dx}\:=\:{x}\:{dv}\: \\ $$$$\int\:\mathrm{2}\:\frac{{dx}}{{x}}\:=\:\int\:\frac{{dv}}{\:\sqrt{{v}}−{v}}\: \\ $$$$\mathrm{ln}\:\mid{x}\mid\:+\:{c}\:=\:\int\:\frac{{dv}}{\:\mathrm{2}\sqrt{{v}}\left(\mathrm{1}−\sqrt{{v}}\right)} \\ $$$$\mathrm{ln}\:\mid{Cx}\:\mid\:=−\:\int\:\frac{{d}\left(\mathrm{1}−\sqrt{{v}}\right)}{\mathrm{1}−\sqrt{{v}}} \\ $$$$\mathrm{ln}\:\mid{Cx}\mid\:=\:−\mathrm{ln}\:\left(\mathrm{1}−\sqrt{{v}}\right) \\ $$$$\mathrm{ln}\:\mid{Cx}\mid\:=\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{1}−\sqrt{{v}}}\right)\Rightarrow{Cx}\:=\:\frac{\mathrm{1}}{\mathrm{1}−\sqrt{\frac{{y}}{{x}}}} \\ $$$$\mathrm{1}−\sqrt{\frac{{y}}{{x}}}\:=\:\frac{\mathrm{1}}{{Cx}}\:\Rightarrow\sqrt{\frac{{y}}{{x}}}\:=\:\frac{{Cx}−\mathrm{1}}{{Cx}} \\ $$$$\frac{{y}}{{x}}\:=\:\left(\frac{{Cx}−\mathrm{1}}{{Cx}}\right)^{\mathrm{2}} \\ $$
Answered by malwaan last updated on 20/Aug/20
(1)∫(x^4 /(1−x^2 ))dx=∫((x^4 −1+1)/(1−x^2 ))dx =∫ [(((x^2 −1)(x^2 +1))/(1−x^2 )) + (1/(1−x^2 ))]dx =∫ [−x^2 −1+ (1/((1−x)(1+x)))]dx =−(x^3 /3) − x + (1/2)ln∣((1+x)/(1−x))∣ + c
$$\left(\mathrm{1}\right)\int\frac{{x}^{\mathrm{4}} }{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\int\frac{{x}^{\mathrm{4}} −\mathrm{1}+\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$=\int\:\left[\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\right]{dx} \\ $$$$=\int\:\left[−{x}^{\mathrm{2}} −\mathrm{1}+\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)}\right]{dx} \\ $$$$=−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:−\:{x}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:+\:{c} \\ $$
Answered by john santu last updated on 20/Aug/20
((⊸JS⊸)/(⊸∼⊸∼)) (5) set y = x^(γ ) → { ((y′=γx^(γ−1) )),((y′′=(γ^2 −γ)x^(γ−2) )),((y′′′=(γ−2)(γ^2 −γ)x^(γ−3) )) :} ⇔((γ−2)(γ^2 −γ)−2(γ^2 −γ)−2γ+8)x^γ =0 (γ^2 −γ)(γ−4)−2γ+8= 0 γ^3 −5γ^2 +2γ+8= 0 (γ+1)(γ^2 −6γ+8) = 0 (γ+1)(γ−2)(γ−4) = 0 → { ((γ=−1)),((γ=2)),((γ=4)) :} General solution is y = C_1 x^(−1) +C_2 x^2 +C_3 x^4
$$\:\:\:\frac{\multimap{JS}\multimap}{\multimap\sim\multimap\sim} \\ $$$$\left(\mathrm{5}\right)\:{set}\:{y}\:=\:{x}^{\gamma\:} \rightarrow\begin{cases}{{y}'=\gamma{x}^{\gamma−\mathrm{1}} }\\{{y}''=\left(\gamma^{\mathrm{2}} −\gamma\right){x}^{\gamma−\mathrm{2}} }\\{{y}'''=\left(\gamma−\mathrm{2}\right)\left(\gamma^{\mathrm{2}} −\gamma\right){x}^{\gamma−\mathrm{3}} }\end{cases} \\ $$$$\Leftrightarrow\left(\left(\gamma−\mathrm{2}\right)\left(\gamma^{\mathrm{2}} −\gamma\right)−\mathrm{2}\left(\gamma^{\mathrm{2}} −\gamma\right)−\mathrm{2}\gamma+\mathrm{8}\right){x}^{\gamma} =\mathrm{0} \\ $$$$\left(\gamma^{\mathrm{2}} −\gamma\right)\left(\gamma−\mathrm{4}\right)−\mathrm{2}\gamma+\mathrm{8}=\:\mathrm{0} \\ $$$$\gamma^{\mathrm{3}} −\mathrm{5}\gamma^{\mathrm{2}} +\mathrm{2}\gamma+\mathrm{8}=\:\mathrm{0} \\ $$$$\left(\gamma+\mathrm{1}\right)\left(\gamma^{\mathrm{2}} −\mathrm{6}\gamma+\mathrm{8}\right)\:=\:\mathrm{0} \\ $$$$\left(\gamma+\mathrm{1}\right)\left(\gamma−\mathrm{2}\right)\left(\gamma−\mathrm{4}\right)\:=\:\mathrm{0}\:\rightarrow\begin{cases}{\gamma=−\mathrm{1}}\\{\gamma=\mathrm{2}}\\{\gamma=\mathrm{4}}\end{cases} \\ $$$$\mathcal{G}{eneral}\:{solution}\:{is}\: \\ $$$${y}\:=\:{C}_{\mathrm{1}} {x}^{−\mathrm{1}} +{C}_{\mathrm{2}} {x}^{\mathrm{2}} +{C}_{\mathrm{3}} {x}^{\mathrm{4}} \\ $$
Answered by john santu last updated on 20/Aug/20
((⊸JS⊸)/(⊸∼⊸∼)) (6) set y = zx →dy = z dx + x dz (x^4 +z^4 x^4 )dx +2x^3 (zx){z dx+x dz }= 0 dx + z^4 dx + 2z{z dx + x dz } = 0 (1+z^4 +2z^2 ) dx = −2zx dz (dx/x) = ((−2z dz)/((z^2 +1)^2 )) ⇒ ∫ (dx/x) = ∫ ((−2z dz)/((z^2 +1)^2 )) ln ∣x∣ + c = −∫ ((d(z^2 +1))/((z^2 +1)^2 )) ln ∣Cx∣ = (1/(z^2 +1)) ; (x^2 /(y^2 +x^2 )) = ln ∣Cx∣
$$\:\:\:\:\frac{\multimap{JS}\multimap}{\multimap\sim\multimap\sim} \\ $$$$\left(\mathrm{6}\right)\:{set}\:{y}\:=\:{zx}\:\rightarrow{dy}\:=\:{z}\:{dx}\:+\:{x}\:{dz} \\ $$$$\left({x}^{\mathrm{4}} +{z}^{\mathrm{4}} {x}^{\mathrm{4}} \right){dx}\:+\mathrm{2}{x}^{\mathrm{3}} \left({zx}\right)\left\{{z}\:{dx}+{x}\:{dz}\:\right\}=\:\mathrm{0} \\ $$$${dx}\:+\:{z}^{\mathrm{4}} {dx}\:+\:\mathrm{2}{z}\left\{{z}\:{dx}\:+\:{x}\:{dz}\:\right\}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{1}+{z}^{\mathrm{4}} +\mathrm{2}{z}^{\mathrm{2}} \right)\:{dx}\:=\:−\mathrm{2}{zx}\:{dz}\: \\ $$$$\frac{{dx}}{{x}}\:=\:\frac{−\mathrm{2}{z}\:{dz}}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\:\int\:\frac{{dx}}{{x}}\:=\:\int\:\frac{−\mathrm{2}{z}\:{dz}}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:\mid{x}\mid\:+\:{c}\:=\:−\int\:\frac{{d}\left({z}^{\mathrm{2}} +\mathrm{1}\right)}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:\mid{Cx}\mid\:=\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} +\mathrm{1}}\:;\:\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:=\:\mathrm{ln}\:\mid{Cx}\mid\: \\ $$
Answered by john santu last updated on 20/Aug/20
⊸J_… S_… ⊸ (3) ∫_0 ^(π^2 /4) sin (√x) dx = ? (solution)set (√x) = t ⇒x = t^2 → { ((dx=2t dt)),((x=(π^2 /4)→t=(π/2))),((x=0 →t = 0)) :} ∫_0 ^(π/2) 2t sin t dt = −∫_0 ^(π/2) 2t d(cos t) = −{ 2t cos t −∫ 2cos t dt } = −2t cos t + 2sin t ]_0 ^(π/2) = 2.
$$\:\:\:\multimap\underset{\ldots} {{J}}\underset{\ldots} {{S}}\multimap \\ $$$$\left(\mathrm{3}\right)\:\underset{\mathrm{0}} {\overset{\pi^{\mathrm{2}} /\mathrm{4}} {\int}}\mathrm{sin}\:\sqrt{{x}}\:{dx}\:=\:? \\ $$$$\left({solution}\right){set}\:\sqrt{{x}}\:=\:{t}\:\Rightarrow{x}\:=\:{t}^{\mathrm{2}} \:\rightarrow\begin{cases}{{dx}=\mathrm{2}{t}\:{dt}}\\{{x}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\rightarrow{t}=\frac{\pi}{\mathrm{2}}}\\{{x}=\mathrm{0}\:\rightarrow{t}\:=\:\mathrm{0}}\end{cases} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{2}{t}\:\mathrm{sin}\:{t}\:{dt}\:=\:−\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{2}{t}\:{d}\left(\mathrm{cos}\:{t}\right) \\ $$$$=\:−\left\{\:\mathrm{2}{t}\:\mathrm{cos}\:{t}\:−\int\:\mathrm{2cos}\:{t}\:{dt}\:\right\}\: \\ $$$$\left.=\:−\mathrm{2}{t}\:\mathrm{cos}\:{t}\:+\:\mathrm{2sin}\:{t}\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\:\mathrm{2}.\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 21/Aug/20
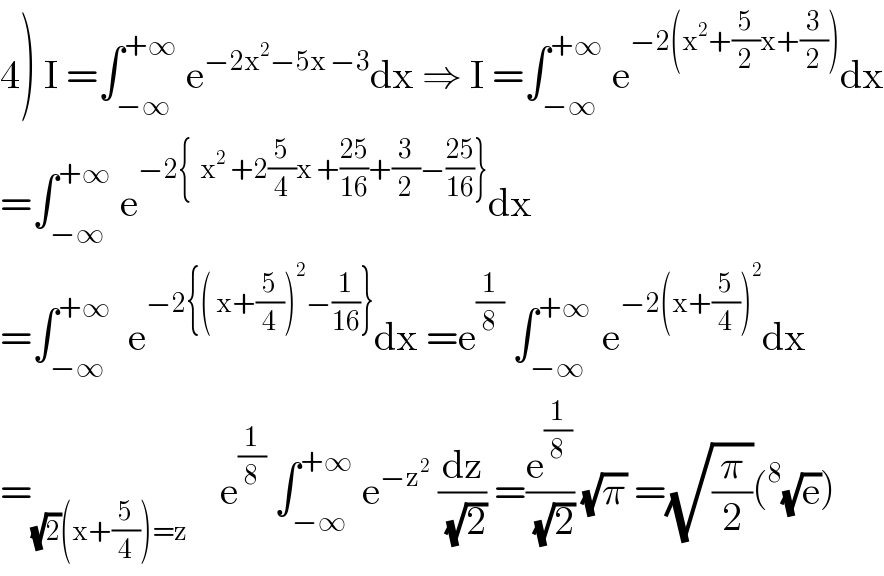
4) I =∫_(−∞) ^(+∞) e^(−2x^2 −5x −3) dx ⇒ I =∫_(−∞) ^(+∞) e^(−2(x^2 +(5/2)x+(3/2))) dx =∫_(−∞) ^(+∞) e^(−2{ x^2 +2(5/4)x +((25)/(16))+(3/2)−((25)/(16))}) dx =∫_(−∞) ^(+∞) e^(−2{( x+(5/4))^2 −(1/(16))}) dx =e^(1/8) ∫_(−∞) ^(+∞ ) e^(−2(x+(5/4))^2 ) dx =_((√2)(x+(5/4))=z) e^(1/8) ∫_(−∞) ^(+∞) e^(−z^2 ) (dz/( (√2))) =(e^(1/8) /( (√2))) (√π) =(√(π/2))(^8 (√e))
$$\left.\mathrm{4}\right)\:\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}\:−\mathrm{3}} \mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{2}}\mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{2}\left\{\:\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{5}}{\mathrm{4}}\mathrm{x}\:+\frac{\mathrm{25}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{25}}{\mathrm{16}}\right\}} \mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\mathrm{e}^{−\mathrm{2}\left\{\left(\:\mathrm{x}+\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{16}}\right\}} \mathrm{dx}\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{8}}} \:\int_{−\infty} ^{+\infty\:} \:\mathrm{e}^{−\mathrm{2}\left(\mathrm{x}+\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} } \mathrm{dx} \\ $$$$=_{\sqrt{\mathrm{2}}\left(\mathrm{x}+\frac{\mathrm{5}}{\mathrm{4}}\right)=\mathrm{z}} \:\:\:\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{8}}} \:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \:\frac{\mathrm{dz}}{\:\sqrt{\mathrm{2}}}\:=\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{8}}} }{\:\sqrt{\mathrm{2}}}\:\sqrt{\pi}\:=\sqrt{\frac{\pi}{\mathrm{2}}}\left(^{\mathrm{8}} \sqrt{\mathrm{e}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *