Question Number 88490 by M±th+et£s last updated on 11/Apr/20
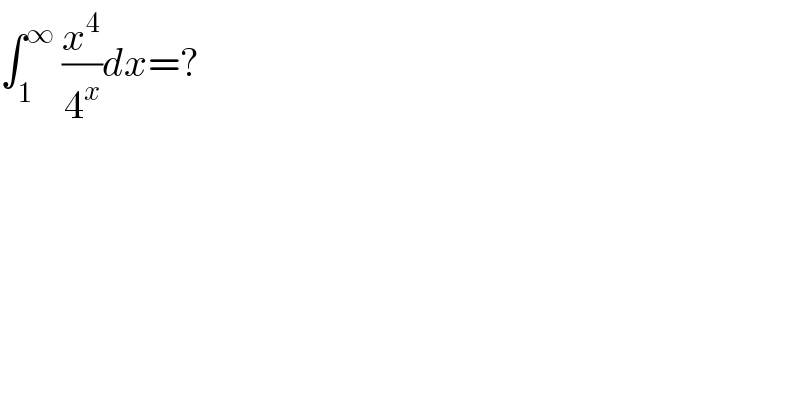
$$\int_{\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{4}} }{\mathrm{4}^{{x}} }{dx}=? \\ $$
Commented by jagoll last updated on 11/Apr/20

Commented by Ar Brandon last updated on 11/Apr/20

$${cool}! \\ $$
Commented by M±th+et£s last updated on 11/Apr/20

$${thanx}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 11/Apr/20
![I =∫_1 ^∞ (x^4 /4^x )dx ⇒ I =∫_1 ^(+∞) x^4 4^(−x) dx we do the changement 4^(−x) =t ⇒e^(−xln(4)) =t ⇒−xln(4) =ln(t) ⇒x =−((ln(t))/(2ln(2))) ⇒ I =−(1/(2ln2))∫_(1/4) ^0 (((lnt)^4 )/(4ln^4 (2))) ×t×(dt/t) =(1/(8ln^5 (2))) ∫_0 ^(1/4) ln^4 (t)dt let u_n =∫ ln^n (t)dt by parts u_n = t ln^n (t)−∫ t n(lnt)^(n−1) (dt/t) =t ln^n (t)−n u_(n−1) ⇒u_4 = t ln^4 (t)−4 u_3 =t ln^4 (t)−4( t ln^3 (t)−3 u_2 ) =t ln^4 (t)−4t ln^3 (t)+12 (t ln^2 (t)−2u_1 ) =t ln^4 (t)−4t ln^3 (t)+12 t ln^2 (t)−24 (t lnt−t) ⇒ ∫_0 ^(1/4) ln^4 (t)dt =[t ln^4 (t)−4t ln^3 (t)+12tln^2 (t)−24t ln(t)+24t]_0 ^(1/4) rest to finish the calculus...](https://www.tinkutara.com/question/Q88597.png)
$${I}\:=\int_{\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{4}} }{\mathrm{4}^{{x}} }{dx}\:\Rightarrow\:{I}\:=\int_{\mathrm{1}} ^{+\infty} \:{x}^{\mathrm{4}} \:\mathrm{4}^{−{x}} \:{dx}\:{we}\:{do}\:{the}\:{changement} \\ $$$$\mathrm{4}^{−{x}} \:={t}\:\Rightarrow{e}^{−{xln}\left(\mathrm{4}\right)} \:={t}\:\Rightarrow−{xln}\left(\mathrm{4}\right)\:={ln}\left({t}\right)\:\Rightarrow{x}\:=−\frac{{ln}\left({t}\right)}{\mathrm{2}{ln}\left(\mathrm{2}\right)}\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}{ln}\mathrm{2}}\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{0}} \:\frac{\left({lnt}\right)^{\mathrm{4}} }{\mathrm{4}{ln}^{\mathrm{4}} \left(\mathrm{2}\right)}\:×{t}×\frac{{dt}}{{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}{ln}^{\mathrm{5}} \left(\mathrm{2}\right)}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{4}}} \:{ln}^{\mathrm{4}} \left({t}\right){dt}\:\:\:\:{let}\:{u}_{{n}} =\int\:{ln}^{{n}} \left({t}\right){dt}\:{by}\:{parts}\: \\ $$$${u}_{{n}} =\:{t}\:{ln}^{{n}} \left({t}\right)−\int\:{t}\:{n}\left({lnt}\right)^{{n}−\mathrm{1}} \:\frac{{dt}}{{t}}\:={t}\:{ln}^{{n}} \left({t}\right)−{n}\:{u}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{u}_{\mathrm{4}} =\:{t}\:{ln}^{\mathrm{4}} \left({t}\right)−\mathrm{4}\:{u}_{\mathrm{3}} ={t}\:{ln}^{\mathrm{4}} \left({t}\right)−\mathrm{4}\left(\:{t}\:{ln}^{\mathrm{3}} \left({t}\right)−\mathrm{3}\:{u}_{\mathrm{2}} \right) \\ $$$$={t}\:{ln}^{\mathrm{4}} \left({t}\right)−\mathrm{4}{t}\:{ln}^{\mathrm{3}} \left({t}\right)+\mathrm{12}\:\left({t}\:{ln}^{\mathrm{2}} \left({t}\right)−\mathrm{2}{u}_{\mathrm{1}} \right) \\ $$$$={t}\:{ln}^{\mathrm{4}} \left({t}\right)−\mathrm{4}{t}\:{ln}^{\mathrm{3}} \left({t}\right)+\mathrm{12}\:{t}\:{ln}^{\mathrm{2}} \left({t}\right)−\mathrm{24}\:\left({t}\:{lnt}−{t}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{4}}} \:{ln}^{\mathrm{4}} \left({t}\right){dt}\:=\left[{t}\:{ln}^{\mathrm{4}} \left({t}\right)−\mathrm{4}{t}\:{ln}^{\mathrm{3}} \left({t}\right)+\mathrm{12}{tln}^{\mathrm{2}} \left({t}\right)−\mathrm{24}{t}\:{ln}\left({t}\right)+\mathrm{24}{t}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${rest}\:{to}\:{finish}\:{the}\:{calculus}… \\ $$
