1-x-4-dx-

Question Number 121384 by john santu last updated on 07/Nov/20

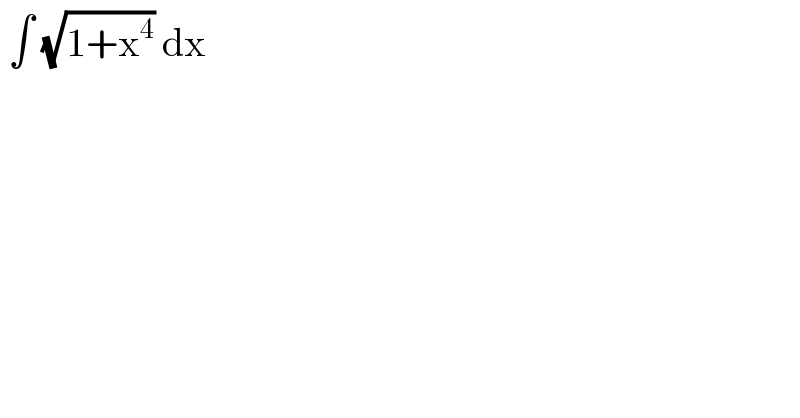
$$\:\int\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx}\: \\ $$

Commented by MJS_new last updated on 07/Nov/20

not possible to solve using only elementary calculus. I guess we need to substitute and transform to get an elliptic integral

$$\mathrm{not}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{using}\:\mathrm{only}\:\mathrm{elementary} \\ $$$$\mathrm{calculus}.\:\mathrm{I}\:\mathrm{guess}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{substitute}\:\mathrm{and} \\ $$$$\mathrm{transform}\:\mathrm{to}\:\mathrm{get}\:\mathrm{an}\:\mathrm{elliptic}\:\mathrm{integral} \\ $$

Commented by peter frank last updated on 08/Nov/20

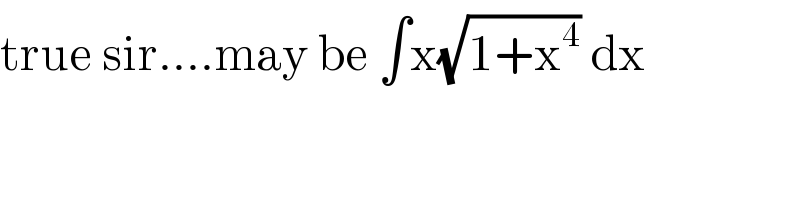
$$\mathrm{true}\:\mathrm{sir}….\mathrm{may}\:\mathrm{be}\:\int\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx} \\ $$

Answered by mathmax by abdo last updated on 07/Nov/20

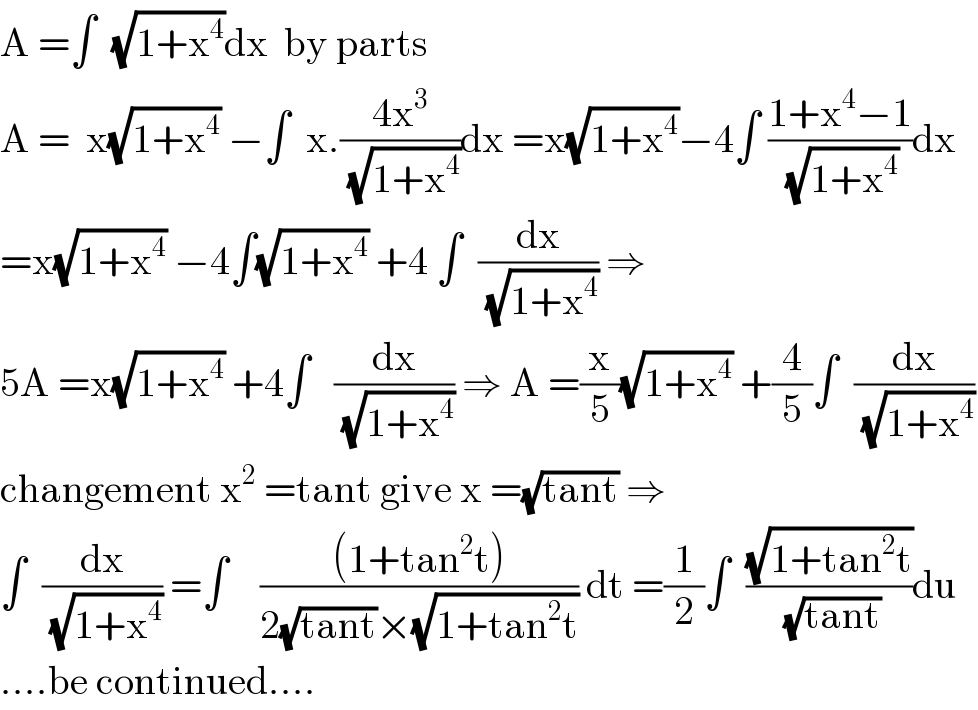
A =∫ (√(1+x^4 ))dx by parts A = x(√(1+x^4 )) −∫ x.((4x^3 )/( (√(1+x^4 ))))dx =x(√(1+x^4 ))−4∫ ((1+x^4 −1)/( (√(1+x^4 ))))dx =x(√(1+x^4 )) −4∫(√(1+x^4 )) +4 ∫ (dx/( (√(1+x^4 )))) ⇒ 5A =x(√(1+x^4 )) +4∫ (dx/( (√(1+x^4 )))) ⇒ A =(x/5)(√(1+x^4 )) +(4/5)∫ (dx/( (√(1+x^4 )))) changement x^2 =tant give x =(√(tant)) ⇒ ∫ (dx/( (√(1+x^4 )))) =∫ (((1+tan^2 t))/(2(√(tant))×(√(1+tan^2 t)))) dt =(1/2)∫ ((√(1+tan^2 t))/( (√(tant))))du ....be continued....

$$\mathrm{A}\:=\int\:\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\mathrm{A}\:=\:\:\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:−\int\:\:\mathrm{x}.\frac{\mathrm{4x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\mathrm{dx}\:=\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }−\mathrm{4}\int\:\frac{\mathrm{1}+\mathrm{x}^{\mathrm{4}} −\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\mathrm{dx} \\ $$$$=\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:−\mathrm{4}\int\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:+\mathrm{4}\:\int\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\:\Rightarrow \\ $$$$\mathrm{5A}\:=\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:+\mathrm{4}\int\:\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\:\Rightarrow\:\mathrm{A}\:=\frac{\mathrm{x}}{\mathrm{5}}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:+\frac{\mathrm{4}}{\mathrm{5}}\int\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }} \\ $$$$\mathrm{changement}\:\mathrm{x}^{\mathrm{2}} \:=\mathrm{tant}\:\mathrm{give}\:\mathrm{x}\:=\sqrt{\mathrm{tant}}\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\:=\int\:\:\:\:\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)}{\mathrm{2}\sqrt{\mathrm{tant}}×\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}}{\:\sqrt{\mathrm{tant}}}\mathrm{du} \\ $$$$….\mathrm{be}\:\mathrm{continued}…. \\ $$

Answered by peter frank last updated on 07/Nov/20

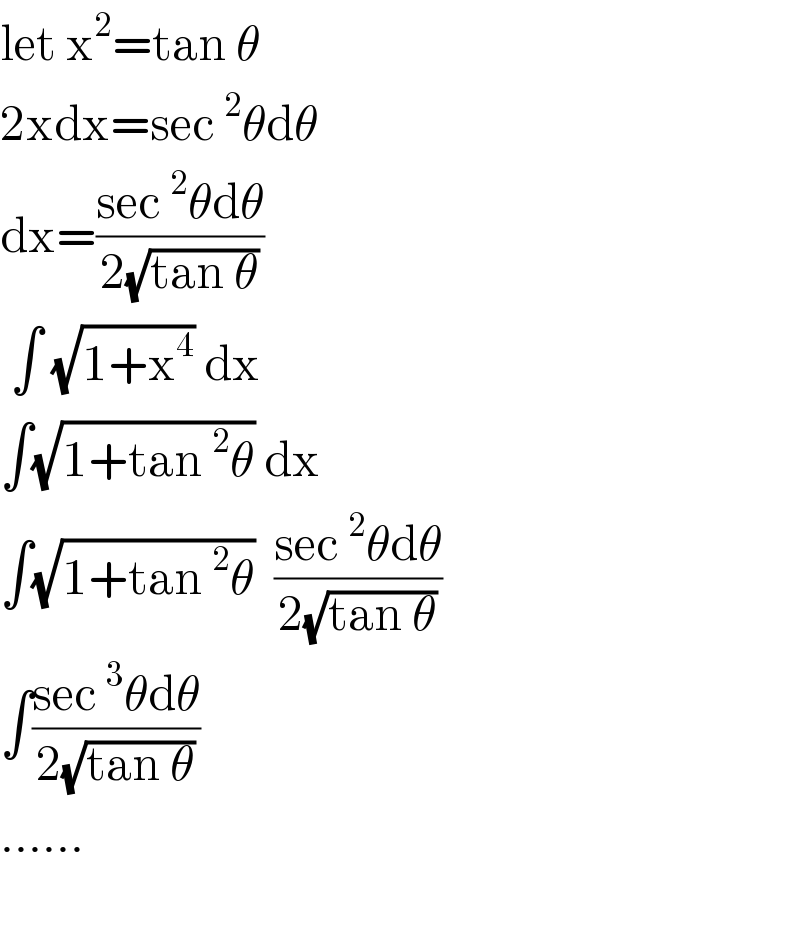
let x^2 =tan θ 2xdx=sec^2 θdθ dx=((sec^2 θdθ)/(2(√(tan θ)))) ∫ (√(1+x^4 )) dx ∫(√(1+tan^2 θ)) dx ∫(√(1+tan^2 θ)) ((sec^2 θdθ)/(2(√(tan θ)))) ∫((sec^3 θdθ)/(2(√(tan θ)))) ......

$$\mathrm{let}\:\mathrm{x}^{\mathrm{2}} =\mathrm{tan}\:\theta \\ $$$$\mathrm{2xdx}=\mathrm{sec}\:^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\mathrm{dx}=\frac{\mathrm{sec}\:^{\mathrm{2}} \theta\mathrm{d}\theta}{\mathrm{2}\sqrt{\mathrm{tan}\:\theta}} \\ $$$$\:\int\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:\mathrm{dx}\: \\ $$$$\int\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}\:\mathrm{dx} \\ $$$$\int\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}\:\:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta\mathrm{d}\theta}{\mathrm{2}\sqrt{\mathrm{tan}\:\theta}} \\ $$$$\int\frac{\mathrm{sec}\:^{\mathrm{3}} \theta\mathrm{d}\theta}{\mathrm{2}\sqrt{\mathrm{tan}\:\theta}} \\ $$$$…… \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply