Question Number 121519 by benjo_mathlover last updated on 09/Nov/20
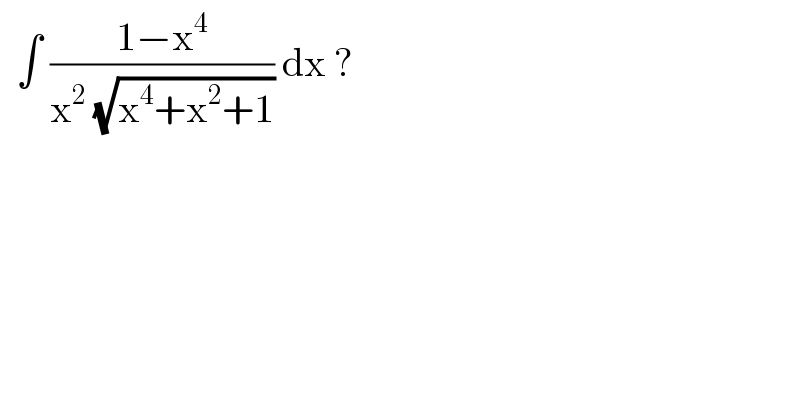
$$\:\:\int\:\frac{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\:\mathrm{dx}\:? \\ $$
Answered by liberty last updated on 09/Nov/20

$$\:\int\:\frac{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{3}} \:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{x}^{−\mathrm{2}} }}\:\mathrm{dx}\:= \\ $$$$\int\:\frac{\mathrm{x}^{−\mathrm{3}} −\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{−\mathrm{2}} +\mathrm{1}}}\:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{v}\:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{−\mathrm{2}} +\mathrm{1}\:\rightarrow\mathrm{dv}\:=\:\mathrm{2x}−\mathrm{2x}^{−\mathrm{3}} \:\mathrm{dx} \\ $$$$\mathrm{dv}\:=\:−\mathrm{2}\left(\mathrm{x}^{−\mathrm{3}} −\mathrm{x}\right)\mathrm{dx}\: \\ $$$$ \\ $$$$\int\:\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{dv}}{\:\sqrt{\mathrm{v}}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{v}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{dv} \\ $$$$=\:−\sqrt{\mathrm{v}}\:+\:\mathrm{c}\:=\:−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{−\mathrm{2}} +\mathrm{1}}\:+\:\mathrm{c} \\ $$$$=\:−\frac{\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{x}}\:+\:\mathrm{c} \\ $$
