Question Number 184031 by SEKRET last updated on 02/Jan/23
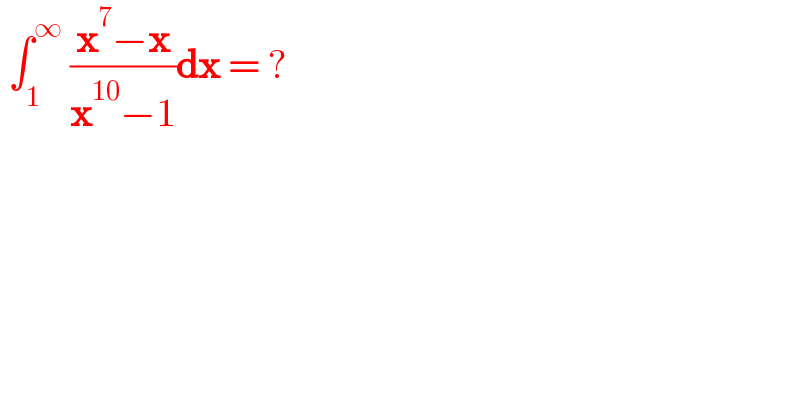
$$\:\int_{\mathrm{1}} ^{\infty} \:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{7}} −\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}^{\mathrm{10}} −\mathrm{1}}\boldsymbol{\mathrm{dx}}\:=\:? \\ $$
Answered by ARUNG_Brandon_MBU last updated on 02/Jan/23
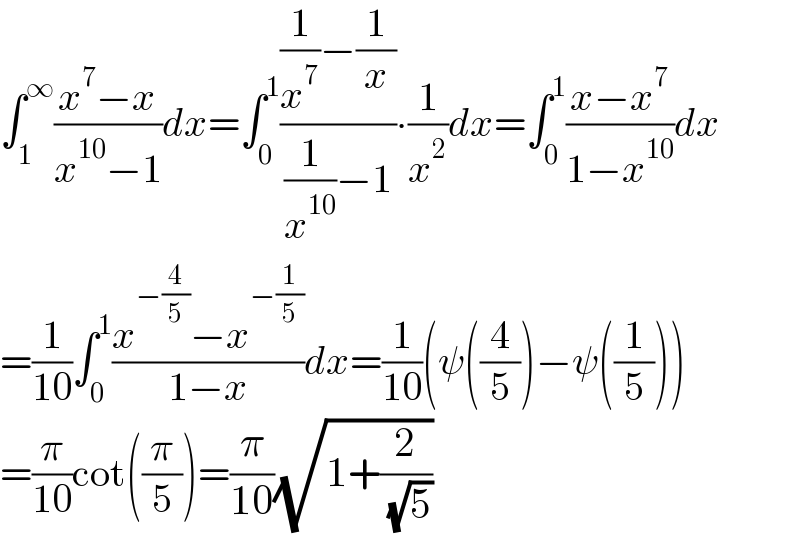
$$\int_{\mathrm{1}} ^{\infty} \frac{{x}^{\mathrm{7}} −{x}}{{x}^{\mathrm{10}} −\mathrm{1}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\frac{\mathrm{1}}{{x}^{\mathrm{7}} }−\frac{\mathrm{1}}{{x}}}{\frac{\mathrm{1}}{{x}^{\mathrm{10}} }−\mathrm{1}}\centerdot\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−{x}^{\mathrm{7}} }{\mathrm{1}−{x}^{\mathrm{10}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{−\frac{\mathrm{4}}{\mathrm{5}}} −{x}^{−\frac{\mathrm{1}}{\mathrm{5}}} }{\mathrm{1}−{x}}{dx}=\frac{\mathrm{1}}{\mathrm{10}}\left(\psi\left(\frac{\mathrm{4}}{\mathrm{5}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{10}}\mathrm{cot}\left(\frac{\pi}{\mathrm{5}}\right)=\frac{\pi}{\mathrm{10}}\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}} \\ $$
Commented by SEKRET last updated on 02/Jan/23
$$\boldsymbol{\mathrm{beatiful}}\:\boldsymbol{\mathrm{solution}}.\:\:\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{sir}} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 02/Jan/23
����
Commented by manxsol last updated on 02/Jan/23
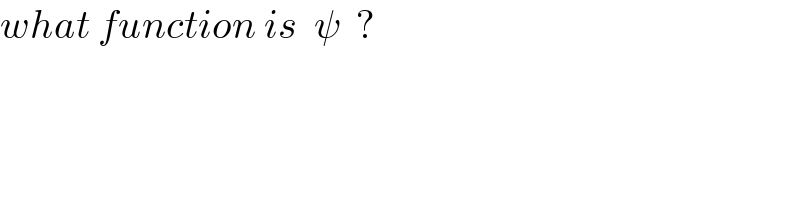
$${what}\:{function}\:{is}\:\:\psi\:\:? \\ $$
Commented by ARUNG_Brandon_MBU last updated on 02/Jan/23
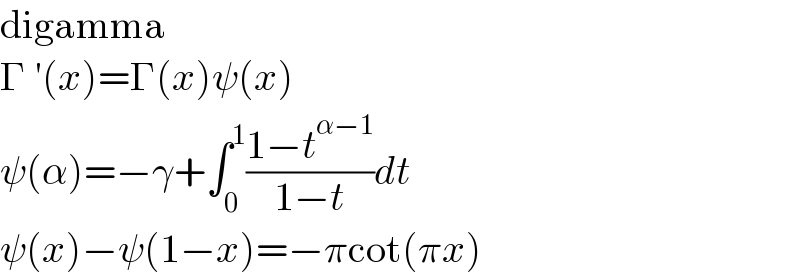
$$\mathrm{digamma} \\ $$$$\Gamma\:'\left({x}\right)=\Gamma\left({x}\right)\psi\left({x}\right) \\ $$$$\psi\left(\alpha\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}^{\alpha−\mathrm{1}} }{\mathrm{1}−{t}}{dt} \\ $$$$\psi\left({x}\right)−\psi\left(\mathrm{1}−{x}\right)=−\pi\mathrm{cot}\left(\pi{x}\right) \\ $$
