1-x-e-1-x-2-dx-

Question Number 146790 by puissant last updated on 15/Jul/21

$$\int\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \mathrm{dx} \\ $$

Answered by Cyriille last updated on 15/Jul/21

I=∫(1/x)e^(-(1/x^2 )) dx let u=e^(-(1/x^2 )) ⇒du=(1/x)e^(-(1/x^2 )) dx ⇒I=∫du=u+k, k∈R ⇒I=e^(-(1/x^2 )) +k, k∈R

$$\boldsymbol{\mathrm{I}}=\int\frac{\mathrm{1}}{{x}}{e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} {dx} \\ $$$${let}\:{u}={e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow{du}=\frac{\mathrm{1}}{{x}}{e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} {dx} \\ $$$$\Rightarrow\boldsymbol{\mathrm{I}}=\int{du}={u}+{k},\:\:\:\:{k}\in\boldsymbol{\mathrm{R}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{I}}={e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} +{k},\:\:\:\:\:\:{k}\in\boldsymbol{\mathrm{R}} \\ $$

Commented by puissant last updated on 15/Jul/21

at the level of the third line what is the derivative sir.?

$$\mathrm{at}\:\mathrm{the}\:\mathrm{level}\:\mathrm{of}\:\mathrm{the}\:\mathrm{third}\:\mathrm{line}\:\mathrm{what}\: \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{derivative}\:\mathrm{sir}.? \\ $$

Commented by mathmax by abdo last updated on 16/Jul/21

(d/dx)(e^(−(1/x^2 )) )=(−(1/x^2 ))^′ e^(−(1/x^2 )) =((2x)/x^4 )e^(−(1/x^2 )) =(2/x^3 )e^(−(1/x^2 )) answer given not correct...!

$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \right)=\left(−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)^{'} \:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:=\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{4}} }\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:\:=\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{answer}\:\mathrm{given}\:\mathrm{not}\:\mathrm{correct}…! \\ $$

Commented by puissant last updated on 16/Jul/21

$$\mathrm{done}\:\mathrm{then}\:\mathrm{sir} \\ $$

Commented by Cyriille last updated on 16/Jul/21

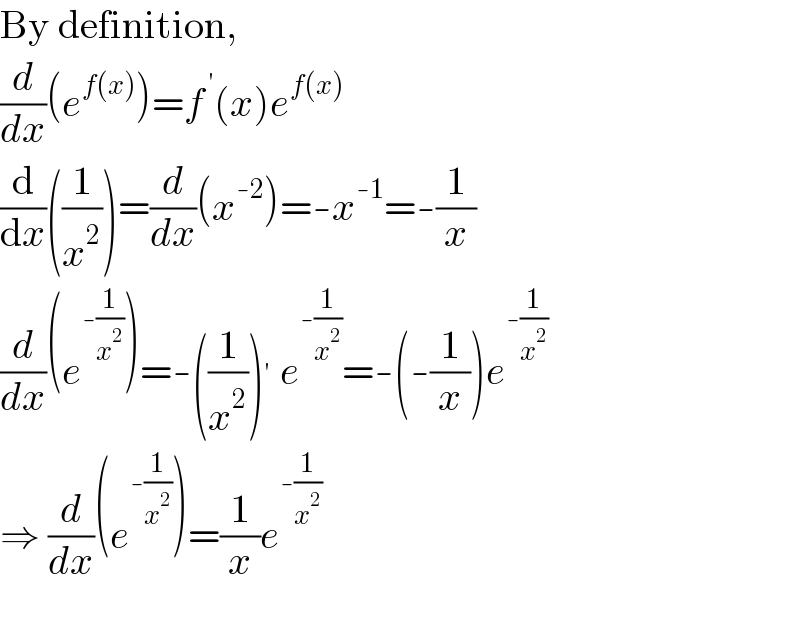
By definition, (d/dx)(e^(f(x)) )=f^( ′) (x)e^(f(x)) (d/dx)((1/x^2 ))=(d/dx)(x^(-2) )=-x^(-1) =-(1/x) (d/dx)(e^(-(1/x^2 )) )=-((1/x^2 ))^′ e^(-(1/x^2 )) =-(-(1/x))e^(-(1/x^2 )) ⇒ (d/dx)(e^(-(1/x^2 )) )=(1/x)e^(-(1/x^2 ))

$$\mathrm{By}\:\mathrm{definition}, \\ $$$$\frac{{d}}{{dx}}\left({e}^{{f}\left({x}\right)} \right)={f}^{\:'} \left({x}\right){e}^{{f}\left({x}\right)} \\ $$$$\frac{\mathrm{d}}{\mathrm{d}{x}}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)=\frac{{d}}{{dx}}\left({x}^{-\mathrm{2}} \right)=-{x}^{-\mathrm{1}} =-\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{d}}{{dx}}\left({e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \right)=-\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{'} \:{e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} =-\left(-\frac{\mathrm{1}}{{x}}\right){e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\frac{{d}}{{dx}}\left({e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \right)=\frac{\mathrm{1}}{{x}}{e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$ \\ $$

Commented by Cyriille last updated on 16/Jul/21

⇒∫d(e^(-(1/x^2 )) )=∫(1/x)e^(-(1/x^2 )) dx , ∫((1/x)e^(-(1/x^2 )) )dx=e^(-(1/x^2 ))

$$\Rightarrow\int{d}\left({e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \right)=\int\frac{\mathrm{1}}{{x}}{e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:{dx} \\ $$$$,\:\int\left(\frac{\mathrm{1}}{{x}}{e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \right){dx}={e}^{-\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$

Commented by mathmax by abdo last updated on 16/Jul/21

d(x^(−2) )=−2x^(−3) =−(2/x^3 ) ⇒d(−x^(−2) )=(2/x^3 )

$$\mathrm{d}\left(\mathrm{x}^{−\mathrm{2}} \right)=−\mathrm{2x}^{−\mathrm{3}} \:=−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }\:\Rightarrow\mathrm{d}\left(−\mathrm{x}^{−\mathrm{2}} \right)=\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} } \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply