Question Number 49144 by AdqhK ÐQeQqQ last updated on 03/Dec/18
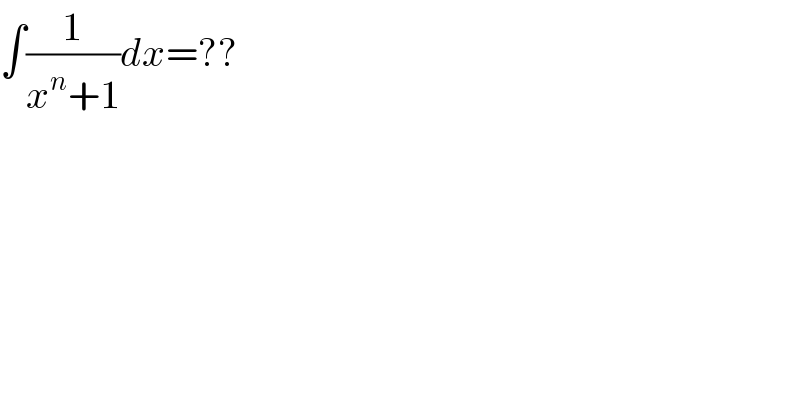
$$\int\frac{\mathrm{1}}{{x}^{{n}} +\mathrm{1}}{dx}=?? \\ $$
Commented by MJS last updated on 04/Dec/18
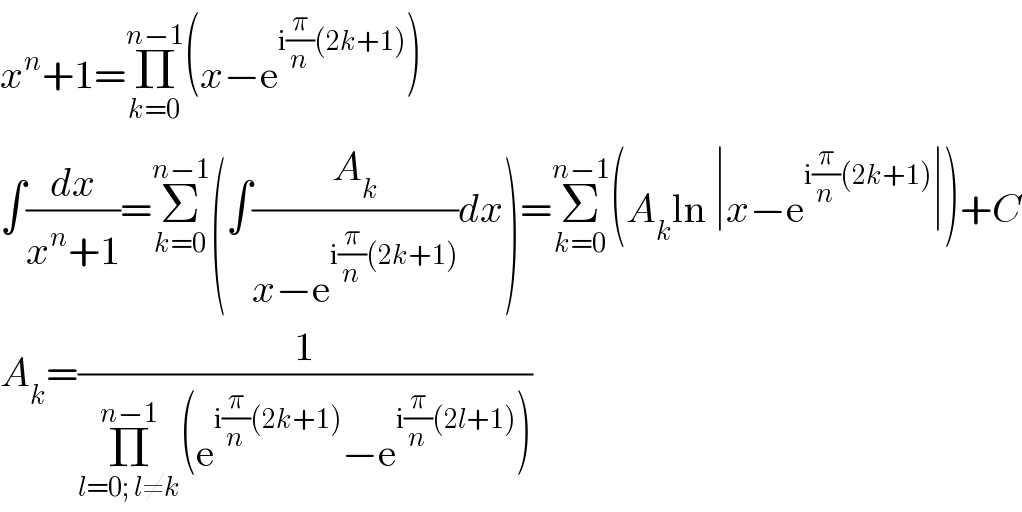
$${x}^{{n}} +\mathrm{1}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({x}−\mathrm{e}^{\mathrm{i}\frac{\pi}{{n}}\left(\mathrm{2}{k}+\mathrm{1}\right)} \right) \\ $$$$\int\frac{{dx}}{{x}^{{n}} +\mathrm{1}}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\int\frac{{A}_{{k}} }{{x}−\mathrm{e}^{\mathrm{i}\frac{\pi}{{n}}\left(\mathrm{2}{k}+\mathrm{1}\right)} }{dx}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left({A}_{{k}} \mathrm{ln}\:\mid{x}−\mathrm{e}^{\mathrm{i}\frac{\pi}{{n}}\left(\mathrm{2}{k}+\mathrm{1}\right)} \mid\right)+{C} \\ $$$${A}_{{k}} =\frac{\mathrm{1}}{\underset{{l}=\mathrm{0};\:{l}\neq{k}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{{n}}\left(\mathrm{2}{k}+\mathrm{1}\right)} −\mathrm{e}^{\mathrm{i}\frac{\pi}{{n}}\left(\mathrm{2}{l}+\mathrm{1}\right)} \right)} \\ $$
Commented by Abdo msup. last updated on 04/Dec/18
![let decompose inside R(x) the fraction F(x)=(1/(x^n +1)) roots of z^n +1 =0 ⇒z^n =e^(iπ) ⇒ if z=r e^(iθ) we get r =1 and nθ=(2k+1)π ⇒θ =(((2k+1)π)/n)?⇒ the roots are z_k = e^((i(2k+1)π)/n) k∈[[0,n−1]] ⇒ F(z) =(1/(Π_(k=0) ^(n−1) (z−z_k ))) =Σ_(k=0) ^(n−1) (λ_k /(z−z_k )) λ_k = (1/(n z_k ^(n−1) )) =(z_k /(−n)) =−(z_k /n) ⇒F(z) =−(1/n)Σ_(k=0) ^(n−1) (z_k /(z−z_k )) ⇒ ∫ F(x)dx =−(1/n) Σ_(k=0) ^(n−1) z_k ∫ (dx/(x−z_k )) let determine ∫ (dx/(x−z_k )) =A_k A_k = ∫ (dx/(x−e^(iθ_k ) )) =∫ (dx/(x−cos(θ_k )−isin(θ_k ))) = ∫ ((x−cos(θ_k )+i sin(θ_k ))/((x−cosθ_k )^2 +sin^2 θ_k ))dx =∫ ((x−cosθ_k )/(x^2 −2xcosθ_k +1))dx +isinθ_k ∫ (dx/((x−cosθ_k )^2 +sin^2 θ_k )) =(1/2)ln(x^2 −2xcosθ_k +1) +isinθ_k ∫ (dx/((x−cosθ_k )^2 +sin^2 θ_k )) but ∫ (dx/((x−cosθ)^2 +sin^2 θ_k )) =_(x−cosθ_k =u sinθ_k ) =∫ ((sinθ_k )/(sin^2 θ_k (1+u^2 )))du =(1/(sinθ_k )) arctan(((x−cosθ_k )/(sinθ_k ))) ⇒ A_k =(1/2)ln(x^2 −2xcosθ_k +1)+i arctan(((x−cosθ_k )/(sinθ_k ))) +C....](https://www.tinkutara.com/question/Q49221.png)
$${let}\:{decompose}\:{inside}\:{R}\left({x}\right)\:{the}\:{fraction}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}^{{n}} \:+\mathrm{1}} \\ $$$${roots}\:{of}\:{z}^{{n}} +\mathrm{1}\:=\mathrm{0}\:\Rightarrow{z}^{{n}} ={e}^{{i}\pi} \:\Rightarrow\:{if}\:{z}={r}\:{e}^{{i}\theta} \:{we}\:{get} \\ $$$${r}\:=\mathrm{1}\:{and}\:{n}\theta=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow\theta\:=\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}?\Rightarrow\:{the}\:{roots}\:{are} \\ $$$${z}_{{k}} =\:{e}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \:\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:\Rightarrow \\ $$$${F}\left({z}\right)\:=\frac{\mathrm{1}}{\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({z}−{z}_{{k}} \right)}\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\lambda_{{k}} }{{z}−{z}_{{k}} } \\ $$$$\lambda_{{k}} =\:\frac{\mathrm{1}}{{n}\:{z}_{{k}} ^{{n}−\mathrm{1}} }\:=\frac{{z}_{{k}} }{−{n}}\:=−\frac{{z}_{{k}} }{{n}}\:\Rightarrow{F}\left({z}\right)\:=−\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{{z}_{{k}} }{{z}−{z}_{{k}} }\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=−\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{z}_{{k}} \:\int\:\:\frac{{dx}}{{x}−{z}_{{k}} }\:{let}\:{determine} \\ $$$$\int\:\:\:\frac{{dx}}{{x}−{z}_{{k}} }\:\:={A}_{{k}} \\ $$$${A}_{{k}} =\:\int\:\:\frac{{dx}}{{x}−{e}^{{i}\theta_{{k}} } }\:\:=\int\:\:\:\frac{{dx}}{{x}−{cos}\left(\theta_{{k}} \right)−{isin}\left(\theta_{{k}} \right)} \\ $$$$=\:\int\:\:\:\:\frac{{x}−{cos}\left(\theta_{{k}} \right)+{i}\:{sin}\left(\theta_{{k}} \right)}{\left({x}−{cos}\theta_{{k}} \right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \theta_{{k}} }{dx} \\ $$$$=\int\:\:\:\frac{{x}−{cos}\theta_{{k}} }{{x}^{\mathrm{2}} \:−\mathrm{2}{xcos}\theta_{{k}} +\mathrm{1}}{dx}\:+{isin}\theta_{{k}} \:\int\:\:\:\frac{{dx}}{\left({x}−{cos}\theta_{{k}} \right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \theta_{{k}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta_{{k}} +\mathrm{1}\right)\:+{isin}\theta_{{k}} \:\:\int\:\:\:\frac{{dx}}{\left({x}−{cos}\theta_{{k}} \right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \theta_{{k}} } \\ $$$${but}\:\int\:\:\:\frac{{dx}}{\left({x}−{cos}\theta\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \theta_{{k}} }\:=_{{x}−{cos}\theta_{{k}} ={u}\:{sin}\theta_{{k}} } \\ $$$$=\int\:\:\:\frac{{sin}\theta_{{k}} }{{sin}^{\mathrm{2}} \theta_{{k}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du}\:=\frac{\mathrm{1}}{{sin}\theta_{{k}} }\:{arctan}\left(\frac{{x}−{cos}\theta_{{k}} }{{sin}\theta_{{k}} }\right)\:\Rightarrow \\ $$$${A}_{{k}} =\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:−\mathrm{2}{xcos}\theta_{{k}} \:+\mathrm{1}\right)+{i}\:{arctan}\left(\frac{{x}−{cos}\theta_{{k}} }{{sin}\theta_{{k}} }\right)\:+{C}…. \\ $$$$ \\ $$
