Menu Close

1-x-tanx-dx-2-tanx-cotx-dx-3-sinx-cosx-sinx-cosx-dx-

Tinku Tara 0 Comments
Pin




Question Number 150696 by tabata last updated on 14/Aug/21
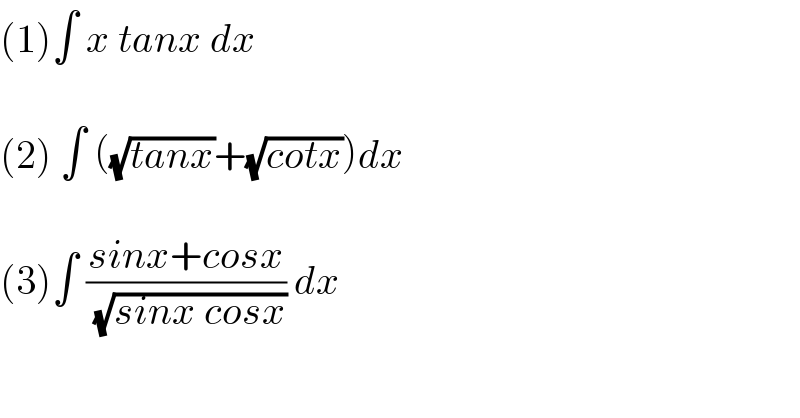
(1)∫ x tanx dx (2) ∫ ((√(tanx))+(√(cotx)))dx (3)∫ ((sinx+cosx)/( (√(sinx cosx)))) dx
$$\left(\mathrm{1}\right)\int\:{x}\:{tanx}\:{dx} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\int\:\left(\sqrt{{tanx}}+\sqrt{{cotx}}\right){dx} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\int\:\frac{{sinx}+{cosx}}{\:\sqrt{{sinx}\:{cosx}}}\:{dx} \\ $$
Commented by Ar Brandon last updated on 14/Aug/21
(2)⇔(3)
$$\left(\mathrm{2}\right)\Leftrightarrow\left(\mathrm{3}\right) \\ $$
Commented by puissant last updated on 14/Aug/21
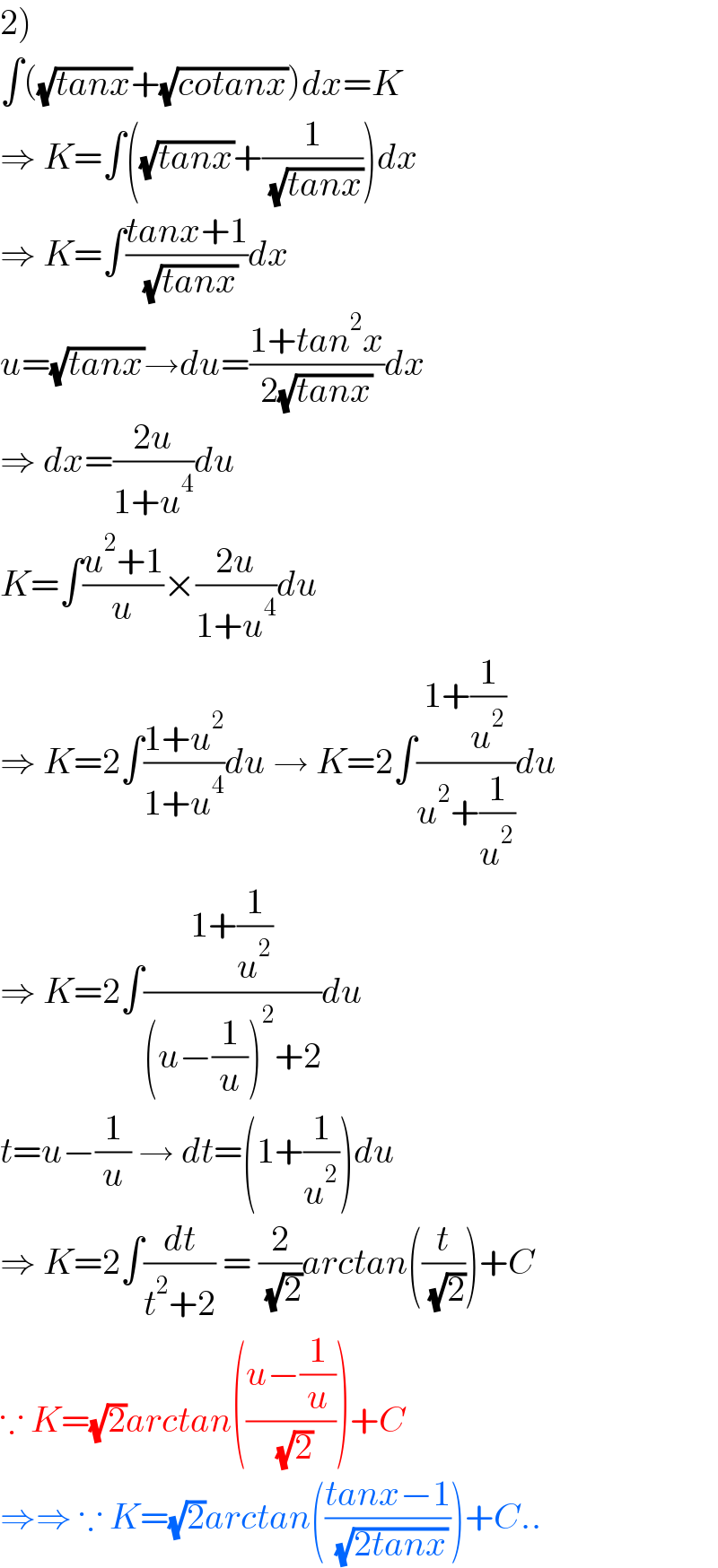
2) ∫((√(tanx))+(√(cotanx)))dx=K ⇒ K=∫((√(tanx))+(1/( (√(tanx)))))dx ⇒ K=∫((tanx+1)/( (√(tanx))))dx u=(√(tanx))→du=((1+tan^2 x)/(2(√(tanx))))dx ⇒ dx=((2u)/(1+u^4 ))du K=∫((u^2 +1)/u)×((2u)/(1+u^4 ))du ⇒ K=2∫((1+u^2 )/(1+u^4 ))du → K=2∫((1+(1/u^2 ))/(u^2 +(1/u^2 )))du ⇒ K=2∫((1+(1/u^2 ))/((u−(1/u))^2 +2))du t=u−(1/u) → dt=(1+(1/u^2 ))du ⇒ K=2∫(dt/(t^2 +2)) = (2/( (√2)))arctan((t/( (√2))))+C ∵ K=(√2)arctan(((u−(1/u))/( (√2))))+C ⇒⇒ ∵ K=(√2)arctan(((tanx−1)/( (√(2tanx)))))+C..
$$\left.\mathrm{2}\right) \\ $$$$\int\left(\sqrt{{tanx}}+\sqrt{{cotanx}}\right){dx}={K} \\ $$$$\Rightarrow\:{K}=\int\left(\sqrt{{tanx}}+\frac{\mathrm{1}}{\:\sqrt{{tanx}}}\right){dx} \\ $$$$\Rightarrow\:{K}=\int\frac{{tanx}+\mathrm{1}}{\:\sqrt{{tanx}}}{dx} \\ $$$${u}=\sqrt{{tanx}}\rightarrow{du}=\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{\mathrm{2}\sqrt{{tanx}}}{dx} \\ $$$$\Rightarrow\:{dx}=\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{4}} }{du} \\ $$$${K}=\int\frac{{u}^{\mathrm{2}} +\mathrm{1}}{{u}}×\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{4}} }{du} \\ $$$$\Rightarrow\:{K}=\mathrm{2}\int\frac{\mathrm{1}+{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{4}} }{du}\:\rightarrow\:{K}=\mathrm{2}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{{u}^{\mathrm{2}} +\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{du} \\ $$$$\Rightarrow\:{K}=\mathrm{2}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{\left({u}−\frac{\mathrm{1}}{{u}}\right)^{\mathrm{2}} +\mathrm{2}}{du} \\ $$$${t}={u}−\frac{\mathrm{1}}{{u}}\:\rightarrow\:{dt}=\left(\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\right){du} \\ $$$$\Rightarrow\:{K}=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}{arctan}\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\right)+{C} \\ $$$$\because\:{K}=\sqrt{\mathrm{2}}{arctan}\left(\frac{{u}−\frac{\mathrm{1}}{{u}}}{\:\sqrt{\mathrm{2}}}\right)+{C} \\ $$$$\Rightarrow\Rightarrow\:\because\:{K}=\sqrt{\mathrm{2}}{arctan}\left(\frac{{tanx}−\mathrm{1}}{\:\sqrt{\mathrm{2}{tanx}}}\right)+{C}.. \\ $$
Answered by Ar Brandon last updated on 14/Aug/21
I=∫(√(tanx))dx , t^2 =tanx ⇒2tdt=(1+t^4 )dx =∫((2t^2 dt)/(1+t^4 ))=∫(((t^2 +1)+(t^2 −1))/(t^4 +1))dt =∫((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt+∫((1−(1/t^2 ))/(t^2 +(1/t^2 )))dt=∫((1+(1/t^2 ))/((t−(1/t))^2 +2))dt+∫((1−(1/t^2 ))/((t+(1/t))^2 −2))dt =∫(du/(u^2 +2))+∫(dv/(v^2 −2))=((arctan(u/(√2)))/( (√2)))−((arctanh(v/(√2)))/( (√2)))+C =(1/( (√2)))arctan(((t^2 −1)/( (√2)t)))−(1/(2(√2)))ln∣((t^2 +(√2)t+1)/(t^2 −(√2)t+1))∣+C =(1/( (√2)))arctan(((tanx−1)/( (√(2tanx)))))−(1/(2(√2)))ln∣((tanx+(√(2tanx))+1)/(tanx−(√(2tanx))+1))∣+C
$$\mathcal{I}=\int\sqrt{\mathrm{tanx}}\mathrm{dx}\:,\:\mathrm{t}^{\mathrm{2}} =\mathrm{tanx}\:\Rightarrow\mathrm{2tdt}=\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)\mathrm{dx} \\ $$$$\:\:\:=\int\frac{\mathrm{2t}^{\mathrm{2}} \mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }=\int\frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:=\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}+\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}=\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt}+\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\mathrm{dt} \\ $$$$\:\:\:=\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2}}+\int\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}=\frac{\mathrm{arctan}\left(\mathrm{u}/\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{arctanh}\left(\mathrm{v}/\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}+\mathrm{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{t}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{t}+\mathrm{1}}\mid+\mathrm{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{tanx}−\mathrm{1}}{\:\sqrt{\mathrm{2tanx}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{tanx}+\sqrt{\mathrm{2tanx}}+\mathrm{1}}{\mathrm{tanx}−\sqrt{\mathrm{2tanx}}+\mathrm{1}}\mid+\mathrm{C} \\ $$
Commented by Ar Brandon last updated on 14/Aug/21
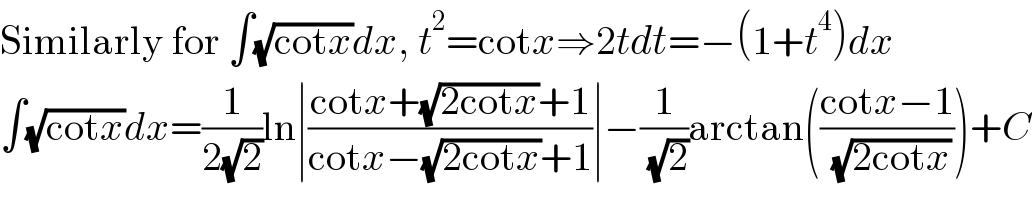
Similarly for ∫(√(cotx))dx, t^2 =cotx⇒2tdt=−(1+t^4 )dx ∫(√(cotx))dx=(1/(2(√2)))ln∣((cotx+(√(2cotx))+1)/(cotx−(√(2cotx))+1))∣−(1/( (√2)))arctan(((cotx−1)/( (√(2cotx)))))+C
$$\mathrm{Similarly}\:\mathrm{for}\:\int\sqrt{\mathrm{cot}{x}}{dx},\:{t}^{\mathrm{2}} =\mathrm{cot}{x}\Rightarrow\mathrm{2}{tdt}=−\left(\mathrm{1}+{t}^{\mathrm{4}} \right){dx} \\ $$$$\int\sqrt{\mathrm{cot}{x}}{dx}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{cot}{x}+\sqrt{\mathrm{2cot}{x}}+\mathrm{1}}{\mathrm{cot}{x}−\sqrt{\mathrm{2cot}{x}}+\mathrm{1}}\mid−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{cot}{x}−\mathrm{1}}{\:\sqrt{\mathrm{2cot}{x}}}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *