Question Number 79233 by jagoll last updated on 23/Jan/20
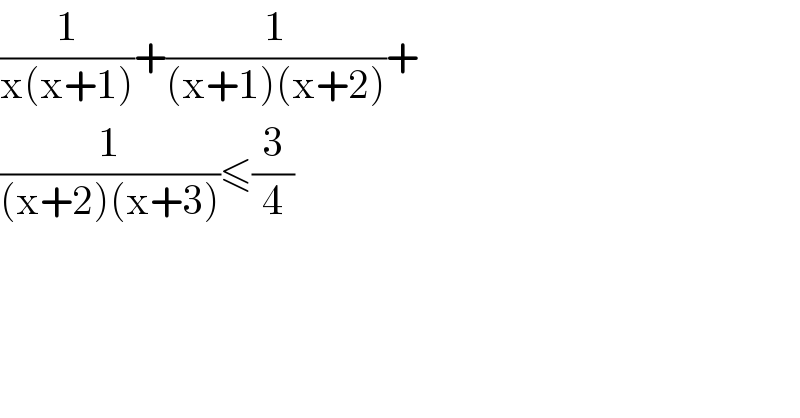
$$\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}+ \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{3}\right)}\leqslant\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by john santu last updated on 23/Jan/20
![(1/x)−(1/(x+1))+(1/(x+1))−(1/(x+2)) +(1/(x+2))−(1/(x+3))≤(3/4) ⇒(1/x)−(1/(x+3))≤(3/4) (4/(4x(x+3)))≤((x(x+3))/(4x(x+3))) ((x^2 +3x−4)/(x(x+3)))≥0 (i) x≠0∧x≠−1∧x≠−2∧x≠−3 (ii) (((x+4)(x−1))/(x(x+3)))≥0 solution ⇒(−∞,−4] ∨(−3,0)∨ [1,∞)∧x≠−1∧x≠−2](https://www.tinkutara.com/question/Q79242.png)
$$\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{2}} \\ $$$$+\frac{\mathrm{1}}{{x}+\mathrm{2}}−\frac{\mathrm{1}}{{x}+\mathrm{3}}\leqslant\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{3}}\leqslant\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{4}}{\mathrm{4}{x}\left({x}+\mathrm{3}\right)}\leqslant\frac{{x}\left({x}+\mathrm{3}\right)}{\mathrm{4}{x}\left({x}+\mathrm{3}\right)} \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}}{{x}\left({x}+\mathrm{3}\right)}\geqslant\mathrm{0}\: \\ $$$$\left({i}\right)\:{x}\neq\mathrm{0}\wedge{x}\neq−\mathrm{1}\wedge{x}\neq−\mathrm{2}\wedge{x}\neq−\mathrm{3} \\ $$$$\left({ii}\right)\:\frac{\left({x}+\mathrm{4}\right)\left({x}−\mathrm{1}\right)}{{x}\left({x}+\mathrm{3}\right)}\geqslant\mathrm{0} \\ $$$${solution}\:\Rightarrow\left(−\infty,−\mathrm{4}\right]\:\vee\left(−\mathrm{3},\mathrm{0}\right)\vee \\ $$$$\left[\mathrm{1},\infty\right)\wedge{x}\neq−\mathrm{1}\wedge{x}\neq−\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 23/Jan/20
![(e) ⇔ (1/x)−(1/(x+1))+(1/(x+1))−(1/(x+2)) +(1/(x+2))−(1/(x+3)) ≤(3/4) ⇔ (1/x)−(1/(x+3)) ≤(3/4) ⇔(3/(x(x+3)))≤(3/4) ⇔(1/(x(x+3)))−(1/4) ≤0 (but x≠0,−1,−2,−3) ⇒((4−x^2 −3x)/(x^2 +3x)) ≤0 ⇔((x^2 +3x−4)/(x^2 +3x)) ≥0 x^2 +3x −4 =0→Δ=9+16 =25 ⇒x_1 =((−3+5)/2) =1 x_2 =((−3−5)/2) =−4 x^2 +3x =0 →x^((1)) =0 and x^((2)) =−3 x −∞ −4 −3 0 1 +∞ x^2 +3x−4 + − − − + x^2 +3x + − − + + Q + + + − + so the set of solution is S =]−∞,−4[∪]−4,3[∪]−3,0[∪[1,+∞[](https://www.tinkutara.com/question/Q79258.png)
$$\left({e}\right)\:\Leftrightarrow\:\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{2}}\:+\frac{\mathrm{1}}{{x}+\mathrm{2}}−\frac{\mathrm{1}}{{x}+\mathrm{3}}\:\leqslant\frac{\mathrm{3}}{\mathrm{4}}\:\Leftrightarrow \\ $$$$\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{3}}\:\leqslant\frac{\mathrm{3}}{\mathrm{4}}\:\:\Leftrightarrow\frac{\mathrm{3}}{{x}\left({x}+\mathrm{3}\right)}\leqslant\frac{\mathrm{3}}{\mathrm{4}}\:\Leftrightarrow\frac{\mathrm{1}}{{x}\left({x}+\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{4}}\:\leqslant\mathrm{0} \\ $$$$\left({but}\:{x}\neq\mathrm{0},−\mathrm{1},−\mathrm{2},−\mathrm{3}\right)\:\Rightarrow\frac{\mathrm{4}−{x}^{\mathrm{2}} −\mathrm{3}{x}}{{x}^{\mathrm{2}} \:+\mathrm{3}{x}}\:\leqslant\mathrm{0}\:\Leftrightarrow\frac{{x}^{\mathrm{2}} \:+\mathrm{3}{x}−\mathrm{4}}{{x}^{\mathrm{2}} \:+\mathrm{3}{x}}\:\geqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}\:−\mathrm{4}\:=\mathrm{0}\rightarrow\Delta=\mathrm{9}+\mathrm{16}\:=\mathrm{25}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{3}+\mathrm{5}}{\mathrm{2}}\:=\mathrm{1} \\ $$$${x}_{\mathrm{2}} =\frac{−\mathrm{3}−\mathrm{5}}{\mathrm{2}}\:=−\mathrm{4} \\ $$$${x}^{\mathrm{2}} \:+\mathrm{3}{x}\:=\mathrm{0}\:\rightarrow{x}^{\left(\mathrm{1}\right)} =\mathrm{0}\:{and}\:{x}^{\left(\mathrm{2}\right)} =−\mathrm{3} \\ $$$${x}\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:+ \\ $$$${x}^{\mathrm{2}} \:+\mathrm{3}{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:+ \\ $$$${Q}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$$${so}\:{the}\:{set}\:{of}\:{solution}\:{is}\: \\ $$$$\left.{S}\:=\right]−\infty,−\mathrm{4}\left[\cup\right]−\mathrm{4},\mathrm{3}\left[\cup\right]−\mathrm{3},\mathrm{0}\left[\cup\left[\mathrm{1},+\infty\left[\right.\right.\right. \\ $$
Commented by mathmax by abdo last updated on 23/Jan/20

$${and}\:{x}\neq−\mathrm{1}\:{and}\:−\mathrm{2} \\ $$
Answered by mr W last updated on 23/Jan/20
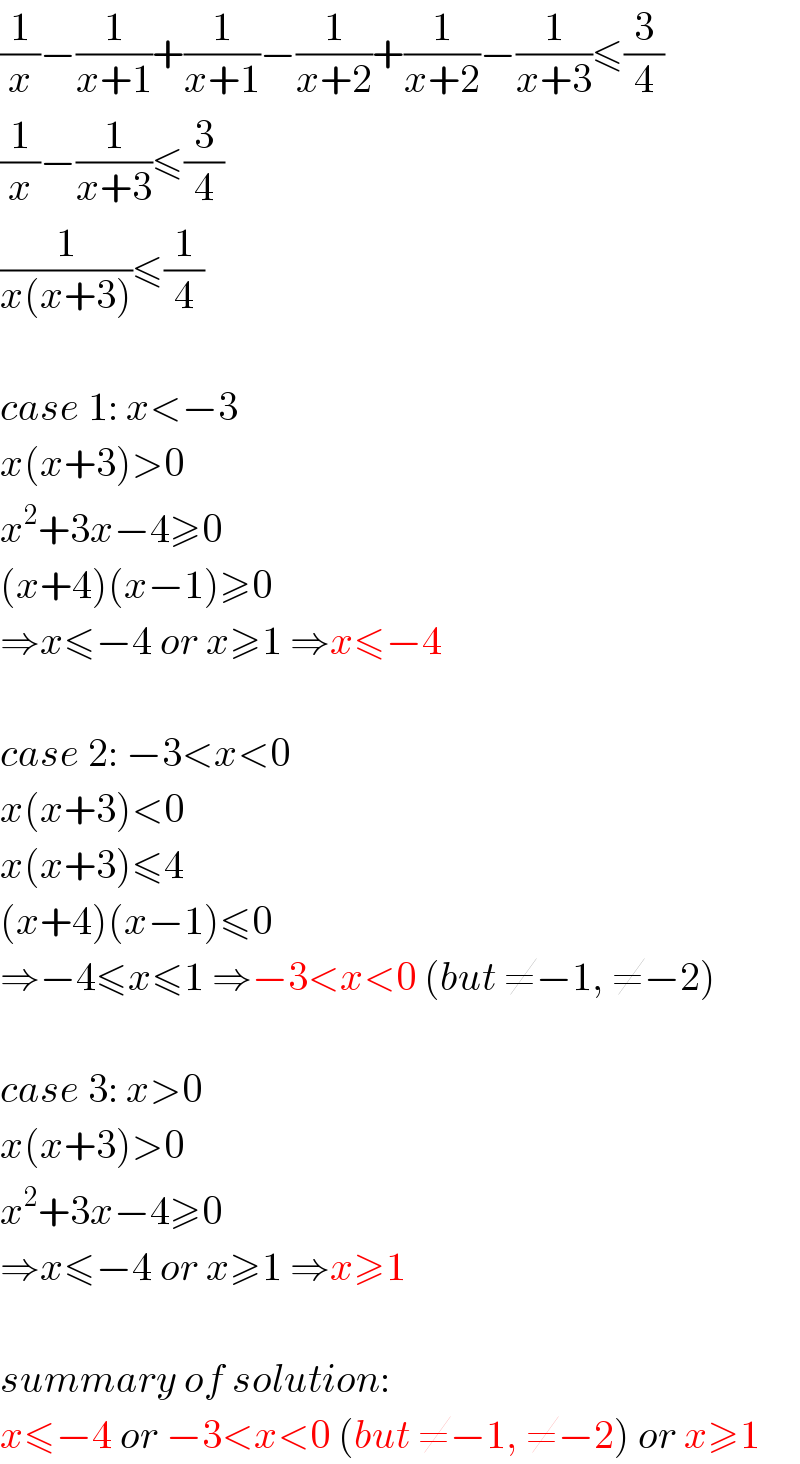
$$\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{2}}+\frac{\mathrm{1}}{{x}+\mathrm{2}}−\frac{\mathrm{1}}{{x}+\mathrm{3}}\leqslant\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{3}}\leqslant\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{{x}\left({x}+\mathrm{3}\right)}\leqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:{x}<−\mathrm{3} \\ $$$${x}\left({x}+\mathrm{3}\right)>\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}\geqslant\mathrm{0} \\ $$$$\left({x}+\mathrm{4}\right)\left({x}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\leqslant−\mathrm{4}\:{or}\:{x}\geqslant\mathrm{1}\:\Rightarrow{x}\leqslant−\mathrm{4} \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:−\mathrm{3}<{x}<\mathrm{0} \\ $$$${x}\left({x}+\mathrm{3}\right)<\mathrm{0} \\ $$$${x}\left({x}+\mathrm{3}\right)\leqslant\mathrm{4} \\ $$$$\left({x}+\mathrm{4}\right)\left({x}−\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow−\mathrm{4}\leqslant{x}\leqslant\mathrm{1}\:\Rightarrow−\mathrm{3}<{x}<\mathrm{0}\:\left({but}\:\neq−\mathrm{1},\:\neq−\mathrm{2}\right) \\ $$$$ \\ $$$${case}\:\mathrm{3}:\:{x}>\mathrm{0} \\ $$$${x}\left({x}+\mathrm{3}\right)>\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\leqslant−\mathrm{4}\:{or}\:{x}\geqslant\mathrm{1}\:\Rightarrow{x}\geqslant\mathrm{1} \\ $$$$ \\ $$$${summary}\:{of}\:{solution}: \\ $$$${x}\leqslant−\mathrm{4}\:{or}\:−\mathrm{3}<{x}<\mathrm{0}\:\left({but}\:\neq−\mathrm{1},\:\neq−\mathrm{2}\right)\:{or}\:{x}\geqslant\mathrm{1} \\ $$
