Question Number 168745 by MikeH last updated on 17/Apr/22
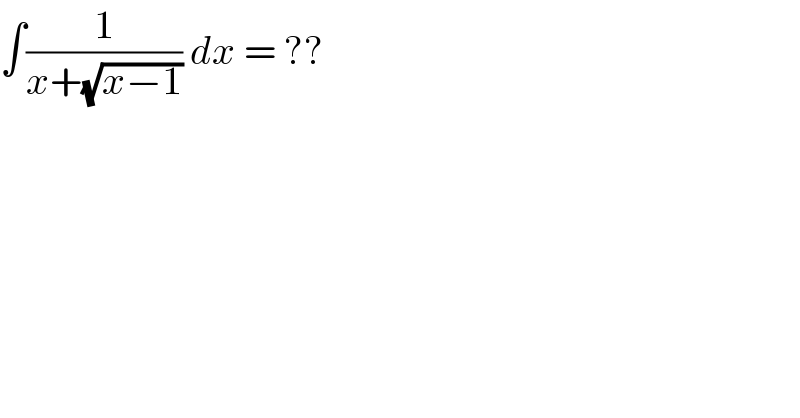
$$\int\frac{\mathrm{1}}{{x}+\sqrt{{x}−\mathrm{1}}}\:{dx}\:=\:?? \\ $$
Commented by safojontoshtemirov last updated on 17/Apr/22
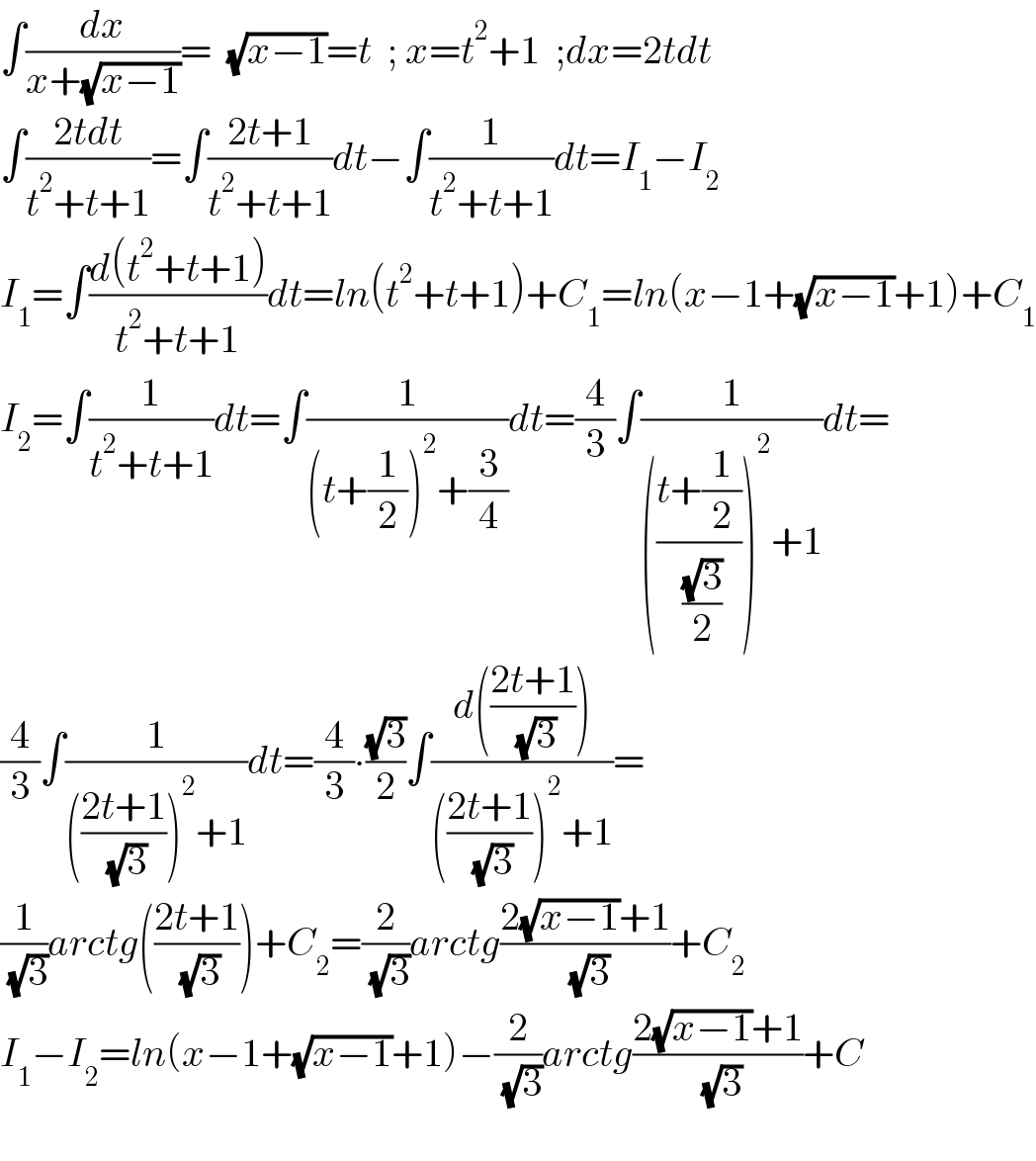
$$\int\frac{{dx}}{{x}+\sqrt{{x}−\mathrm{1}}}=\:\:\sqrt{{x}−\mathrm{1}}={t}\:\:;\:{x}={t}^{\mathrm{2}} +\mathrm{1}\:\:;{dx}=\mathrm{2}{tdt} \\ $$$$\int\frac{\mathrm{2}{tdt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}=\int\frac{\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}−\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}={I}_{\mathrm{1}} −{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\int\frac{{d}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}={ln}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)+{C}_{\mathrm{1}} ={ln}\left({x}−\mathrm{1}+\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)+{C}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}=\int\frac{\mathrm{1}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{dt}=\frac{\mathrm{4}}{\mathrm{3}}\int\frac{\mathrm{1}}{\left(\frac{{t}+\frac{\mathrm{1}}{\mathrm{2}}}{\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\int\frac{\mathrm{1}}{\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}}{dt}=\frac{\mathrm{4}}{\mathrm{3}}\centerdot\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\frac{{d}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}{\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}}= \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{arctg}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{C}_{\mathrm{2}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{arctg}\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}+{C}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} −{I}_{\mathrm{2}} ={ln}\left({x}−\mathrm{1}+\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{arctg}\frac{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}+{C} \\ $$$$ \\ $$
Answered by blackmamba last updated on 17/Apr/22
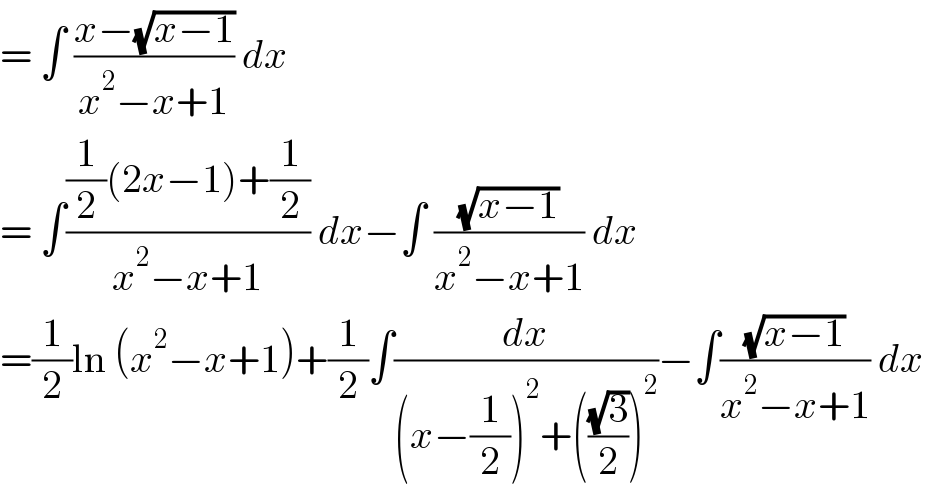
$$=\:\int\:\frac{{x}−\sqrt{{x}−\mathrm{1}}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx}\: \\ $$$$=\:\int\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx}−\int\:\frac{\sqrt{{x}−\mathrm{1}}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }−\int\frac{\sqrt{{x}−\mathrm{1}}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx}\: \\ $$
