Question Number 121066 by Jamshidbek2311 last updated on 05/Nov/20
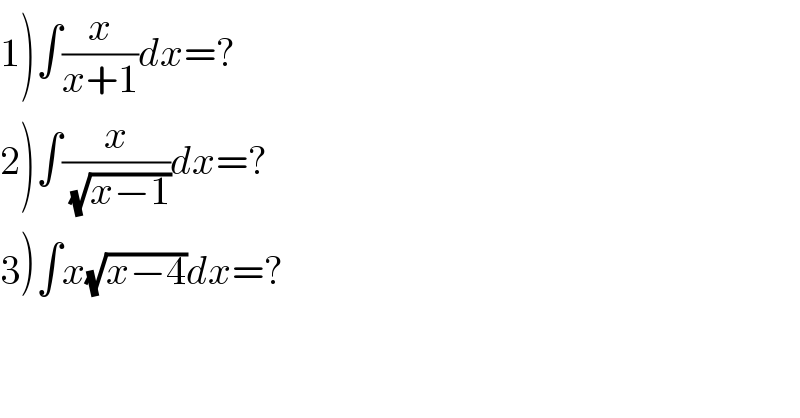
$$\left.\mathrm{1}\right)\int\frac{{x}}{{x}+\mathrm{1}}{dx}=? \\ $$$$\left.\mathrm{2}\right)\int\frac{{x}}{\:\sqrt{{x}−\mathrm{1}}}{dx}=? \\ $$$$\left.\mathrm{3}\right)\int{x}\sqrt{{x}−\mathrm{4}}{dx}=\overset{} {?} \\ $$$$ \\ $$
Commented by liberty last updated on 05/Nov/20
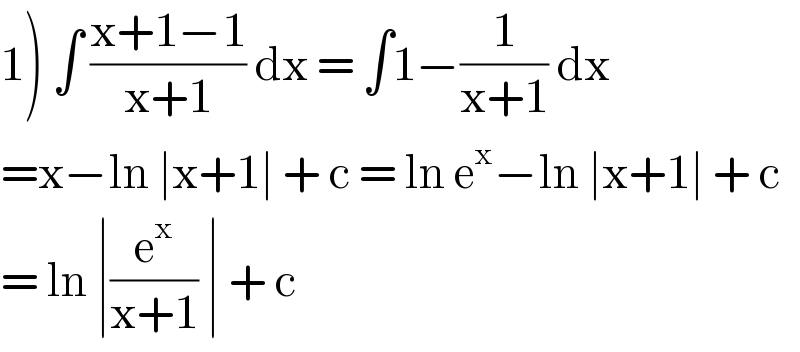
$$\left.\mathrm{1}\right)\:\int\:\frac{\mathrm{x}+\mathrm{1}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\mathrm{dx}\:=\:\int\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\mathrm{dx} \\ $$$$=\mathrm{x}−\mathrm{ln}\:\mid\mathrm{x}+\mathrm{1}\mid\:+\:\mathrm{c}\:=\:\mathrm{ln}\:\mathrm{e}^{\mathrm{x}} −\mathrm{ln}\:\mid\mathrm{x}+\mathrm{1}\mid\:+\:\mathrm{c} \\ $$$$=\:\mathrm{ln}\:\mid\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{x}+\mathrm{1}}\:\mid\:+\:\mathrm{c}\: \\ $$
Answered by Dwaipayan Shikari last updated on 05/Nov/20
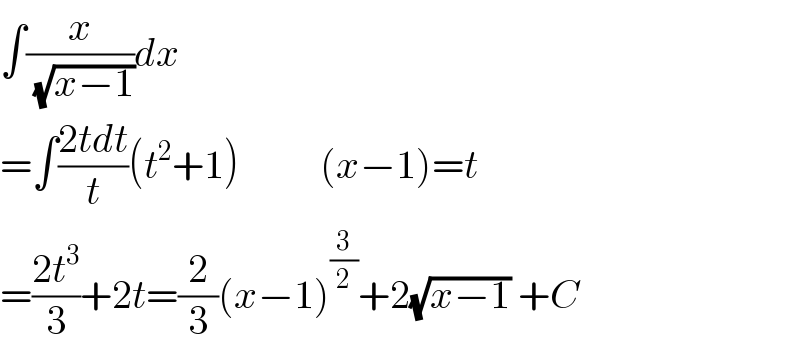
$$\int\frac{{x}}{\:\sqrt{{x}−\mathrm{1}}}{dx} \\ $$$$=\int\frac{\mathrm{2}{tdt}}{{t}}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\left({x}−\mathrm{1}\right)={t} \\ $$$$=\frac{\mathrm{2}{t}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{2}{t}=\frac{\mathrm{2}}{\mathrm{3}}\left({x}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{2}\sqrt{{x}−\mathrm{1}}\:+{C} \\ $$
Answered by bramlexs22 last updated on 05/Nov/20
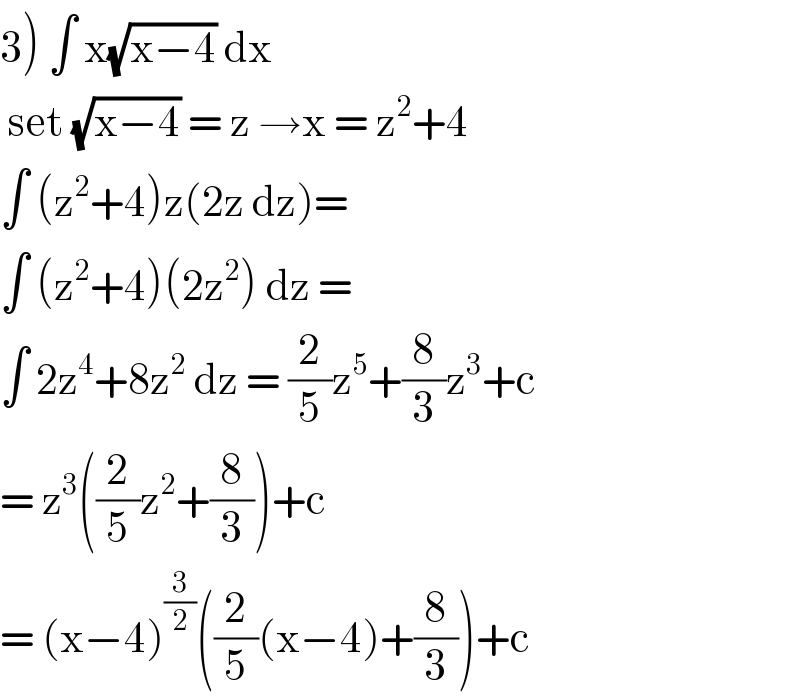
$$\left.\mathrm{3}\right)\:\int\:\mathrm{x}\sqrt{\mathrm{x}−\mathrm{4}}\:\mathrm{dx}\: \\ $$$$\:\mathrm{set}\:\sqrt{\mathrm{x}−\mathrm{4}}\:=\:\mathrm{z}\:\rightarrow\mathrm{x}\:=\:\mathrm{z}^{\mathrm{2}} +\mathrm{4} \\ $$$$\int\:\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)\mathrm{z}\left(\mathrm{2z}\:\mathrm{dz}\right)= \\ $$$$\int\:\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)\left(\mathrm{2z}^{\mathrm{2}} \right)\:\mathrm{dz}\:= \\ $$$$\int\:\mathrm{2z}^{\mathrm{4}} +\mathrm{8z}^{\mathrm{2}} \:\mathrm{dz}\:=\:\frac{\mathrm{2}}{\mathrm{5}}\mathrm{z}^{\mathrm{5}} +\frac{\mathrm{8}}{\mathrm{3}}\mathrm{z}^{\mathrm{3}} +\mathrm{c} \\ $$$$=\:\mathrm{z}^{\mathrm{3}} \left(\frac{\mathrm{2}}{\mathrm{5}}\mathrm{z}^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{3}}\right)+\mathrm{c} \\ $$$$=\:\left(\mathrm{x}−\mathrm{4}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{x}−\mathrm{4}\right)+\frac{\mathrm{8}}{\mathrm{3}}\right)+\mathrm{c} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Nov/20
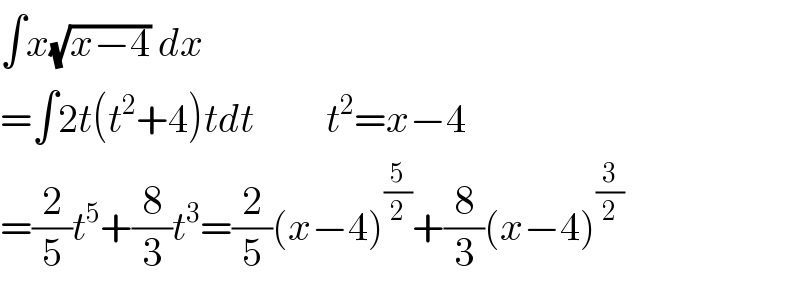
$$\int{x}\sqrt{{x}−\mathrm{4}}\:{dx} \\ $$$$=\int\mathrm{2}{t}\left({t}^{\mathrm{2}} +\mathrm{4}\right){tdt}\:\:\:\:\:\:\:\:\:{t}^{\mathrm{2}} ={x}−\mathrm{4} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}{t}^{\mathrm{5}} +\frac{\mathrm{8}}{\mathrm{3}}{t}^{\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{5}}\left({x}−\mathrm{4}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} +\frac{\mathrm{8}}{\mathrm{3}}\left({x}−\mathrm{4}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$
