Menu Close

1-x-x-2-x-1-dx-2-1-x-1-x-2-x-1-dx-3-x-2-4x-10-dx-

Tinku Tara 0 Comments
Pin




Question Number 89146 by M±th+et£s last updated on 15/Apr/20
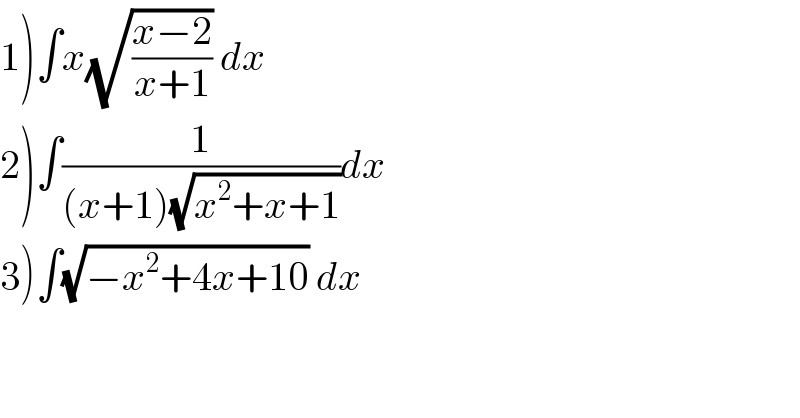
1)∫x(√((x−2)/(x+1))) dx 2)∫(1/((x+1)(√(x^2 +x+1))))dx 3)∫(√(−x^2 +4x+10)) dx
$$\left.\mathrm{1}\right)\int{x}\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}\:{dx} \\ $$$$\left.\mathrm{2}\right)\int\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx} \\ $$$$\left.\mathrm{3}\right)\int\sqrt{−{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{10}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 16/Apr/20
1) I =∫x(√((x−2)/(x+1)))dx changement (√((x−2)/(x+1)))=t give ((x−2)/(x+1))=t^2 ⇒ x−2=t^2 x +t^2 ⇒(1−t^2 )x =t^2 +2 ⇒x=((t^2 +2)/(1−t^2 )) ⇒ (dx/dt) =((2t(1−t^2 )+2t(t^2 +2))/((1−t^2 )^2 )) =((2t−2t^3 +2t^3 +4t)/((1−t^2 )^2 )) =((6t)/((t^2 −1)^2 )) ⇒I =∫((t^2 +2)/(1−t^2 ))×t×((6t)/((t^2 −1)^2 ))dt =−6 ∫ ((t^3 +2t)/((t^2 −1)^3 ))dt ⇒ −(1/6)I =∫ ((t^3 +2t)/((t−1)^3 (t+1)^3 ))dt =∫ ((t^3 +2t)/((((t−1)/(t+1)))^3 (t+1)^6 )) we do the changement ((t−1)/(t+1)) =u ⇒t−1 =ut+u ⇒(1−u)t =u+1 ⇒t =((1+u)/(1−u)) ⇒ (dt/du) =((1−u+1+u)/((1−u)^2 )) =(2/((u−1)^2 )) also t+1 =((1+u)/(1−u)) +1 =((1+u+1−u)/(1−u)) =(2/(1−u)) ⇒ −(1/6)I = ∫ (((((1+u)^3 )/((1−u)^3 ))+2((1+u)/(1−u)))/(u^3 ((2/(1−u)))^6 ))×((2du)/((u−1)^2 )) =(1/2^5 ) ∫ (((1+u)^3 +2(1+u)(1−u)^2 )/((1−u)^3 u^3 ))×(u−1)^4 du =−(1/2^5 )∫ (((u−1){ u^3 +3u^2 +3u +1 +2(u+1)(u^2 −2u +1)})/u^3 )du ⇒I =(6/2^5 ) ∫ (((u−1){ u^3 +3u^2 +3u +1 +2(u^3 −2u^2 +u+u^2 −2u+1)})/u^3 )du =(3/(16))∫ (((u−1){u^3 +3u^2 +3u+1 +(2u^3 −2u^2 −2u+2)})/u^3 )du =(3/(16))∫ (((u−1){5u^3 +u^2 +u +3})/u^3 )du =(3/(16))∫ ((5u^4 +u^3 +u^2 +3u −5u^3 −u^2 −u−3)/u^3 ) du =(3/(16))∫ ((5u^4 −4u^3 +2u−3)/u^3 )du =((15)/(16)) ∫u du −(3/4) ∫ du +(3/8) ∫ (du/u^2 )−(9/(16))∫ (du/u^3 ) =((15)/(32))u^2 −(3/4)u −(3/(8u)) +(9/(32u^2 )) +C =((15)/(32))(((t−1)/(t+1)))^2 −(3/4)(((t−1)/(t+1))) −(3/8)(((t+1)/(t−1))) +(9/(32))(((t+1)/(t−1)))^2 +C =((15)/(32))((((√((x−2)/(x+1)))−1)/( (√(((x−2)/(x+1))+1)))))^2 −(3/4)((((√((x−2)/(x+1)))−1)/( (√((x−2)/(x+1)))+1)))−(3/8)((((√((x−2)/(x+1)))+1)/( (√((x−2)/(x+1)))−1))) +(9/(32))((((√((x−2)/(x+1)))+1)/( (√(((x−2)/(x+1))−1)))))^2 +C
$$\left.\mathrm{1}\right)\:{I}\:=\int{x}\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}{dx}\:{changement}\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}={t}\:{give}\:\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}−\mathrm{2}={t}^{\mathrm{2}} {x}\:+{t}^{\mathrm{2}} \:\Rightarrow\left(\mathrm{1}−{t}^{\mathrm{2}} \right){x}\:={t}^{\mathrm{2}} \:+\mathrm{2}\:\Rightarrow{x}=\frac{{t}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{1}−{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\mathrm{2}{t}\left({t}^{\mathrm{2}} \:+\mathrm{2}\right)}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{4}{t}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{6}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{I}\:=\int\frac{{t}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{1}−{t}^{\mathrm{2}} }×{t}×\frac{\mathrm{6}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=−\mathrm{6}\:\int\:\:\frac{{t}^{\mathrm{3}} \:+\mathrm{2}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }{dt}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}{I}\:\:=\int\:\:\frac{{t}^{\mathrm{3}} \:+\mathrm{2}{t}}{\left({t}−\mathrm{1}\right)^{\mathrm{3}} \left({t}+\mathrm{1}\right)^{\mathrm{3}} }{dt}\:=\int\:\:\frac{{t}^{\mathrm{3}} \:+\mathrm{2}{t}}{\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)^{\mathrm{3}} \left({t}+\mathrm{1}\right)^{\mathrm{6}} }\:{we}\:{do}\:{the}\:{changement} \\ $$$$\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\:={u}\:\Rightarrow{t}−\mathrm{1}\:={ut}+{u}\:\Rightarrow\left(\mathrm{1}−{u}\right){t}\:={u}+\mathrm{1}\:\Rightarrow{t}\:=\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\:\Rightarrow \\ $$$$\frac{{dt}}{{du}}\:=\frac{\mathrm{1}−{u}+\mathrm{1}+{u}}{\left(\mathrm{1}−{u}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\left({u}−\mathrm{1}\right)^{\mathrm{2}} }\:\:{also}\:{t}+\mathrm{1}\:=\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\:+\mathrm{1}\:=\frac{\mathrm{1}+{u}+\mathrm{1}−{u}}{\mathrm{1}−{u}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−{u}}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}{I}\:=\:\int\:\:\:\frac{\frac{\left(\mathrm{1}+{u}\right)^{\mathrm{3}} }{\left(\mathrm{1}−{u}\right)^{\mathrm{3}} }+\mathrm{2}\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}}{{u}^{\mathrm{3}} \left(\frac{\mathrm{2}}{\mathrm{1}−{u}}\right)^{\mathrm{6}} }×\frac{\mathrm{2}{du}}{\left({u}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\:\int\:\:\:\:\frac{\left(\mathrm{1}+{u}\right)^{\mathrm{3}} \:+\mathrm{2}\left(\mathrm{1}+{u}\right)\left(\mathrm{1}−{u}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{u}\right)^{\mathrm{3}} \:{u}^{\mathrm{3}} }×\left({u}−\mathrm{1}\right)^{\mathrm{4}} \:{du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\int\:\:\:\frac{\left({u}−\mathrm{1}\right)\left\{\:{u}^{\mathrm{3}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{3}{u}\:+\mathrm{1}\:+\mathrm{2}\left({u}+\mathrm{1}\right)\left({u}^{\mathrm{2}} −\mathrm{2}{u}\:+\mathrm{1}\right)\right\}}{{u}^{\mathrm{3}} }{du} \\ $$$$\Rightarrow{I}\:=\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{5}} }\:\int\:\frac{\left({u}−\mathrm{1}\right)\left\{\:{u}^{\mathrm{3}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{3}{u}\:+\mathrm{1}\:+\mathrm{2}\left({u}^{\mathrm{3}} −\mathrm{2}{u}^{\mathrm{2}} +{u}+{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{1}\right)\right\}}{{u}^{\mathrm{3}} }{du} \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\int\:\frac{\left({u}−\mathrm{1}\right)\left\{{u}^{\mathrm{3}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{3}{u}+\mathrm{1}\:+\left(\mathrm{2}{u}^{\mathrm{3}} −\mathrm{2}{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{2}\right)\right\}}{{u}^{\mathrm{3}} }{du} \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\int\:\:\frac{\left({u}−\mathrm{1}\right)\left\{\mathrm{5}{u}^{\mathrm{3}} +{u}^{\mathrm{2}} +{u}\:+\mathrm{3}\right\}}{{u}^{\mathrm{3}} }{du} \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\int\:\frac{\mathrm{5}{u}^{\mathrm{4}} \:+{u}^{\mathrm{3}} +{u}^{\mathrm{2}} +\mathrm{3}{u}\:−\mathrm{5}{u}^{\mathrm{3}} −{u}^{\mathrm{2}} −{u}−\mathrm{3}}{{u}^{\mathrm{3}} }\:{du} \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\int\:\frac{\mathrm{5}{u}^{\mathrm{4}} −\mathrm{4}{u}^{\mathrm{3}} +\mathrm{2}{u}−\mathrm{3}}{{u}^{\mathrm{3}} }{du} \\ $$$$=\frac{\mathrm{15}}{\mathrm{16}}\:\int{u}\:{du}\:−\frac{\mathrm{3}}{\mathrm{4}}\:\int\:{du}\:\:+\frac{\mathrm{3}}{\mathrm{8}}\:\int\:\frac{{du}}{{u}^{\mathrm{2}} }−\frac{\mathrm{9}}{\mathrm{16}}\int\:\frac{{du}}{{u}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{15}}{\mathrm{32}}{u}^{\mathrm{2}} \:−\frac{\mathrm{3}}{\mathrm{4}}{u}\:\:−\frac{\mathrm{3}}{\mathrm{8}{u}}\:+\frac{\mathrm{9}}{\mathrm{32}{u}^{\mathrm{2}} }\:+{C} \\ $$$$=\frac{\mathrm{15}}{\mathrm{32}}\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)\:−\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\right)\:+\frac{\mathrm{9}}{\mathrm{32}}\left(\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\right)^{\mathrm{2}} \:+{C} \\ $$$$=\frac{\mathrm{15}}{\mathrm{32}}\left(\frac{\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}−\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}+\mathrm{1}}}\right)^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}−\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}+\mathrm{1}}\right)−\frac{\mathrm{3}}{\mathrm{8}}\left(\frac{\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}+\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}−\mathrm{1}}\right) \\ $$$$+\frac{\mathrm{9}}{\mathrm{32}}\left(\frac{\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}+\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}−\mathrm{1}}}\right)^{\mathrm{2}} \:+{C} \\ $$
Commented by mathmax by abdo last updated on 16/Apr/20
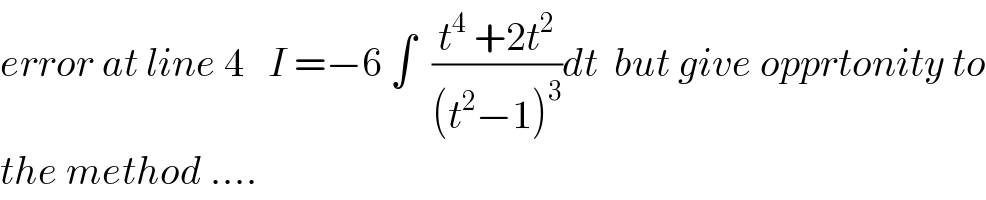
error at line 4 I =−6 ∫ ((t^4 +2t^2 )/((t^2 −1)^3 ))dt but give opprtonity to the method ....
$${error}\:{at}\:{line}\:\mathrm{4}\:\:\:{I}\:=−\mathrm{6}\:\int\:\:\frac{{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }{dt}\:\:{but}\:{give}\:{opprtonity}\:{to} \\ $$$${the}\:{method}\:…. \\ $$
Commented by M±th+et£s last updated on 16/Apr/20
thank you for the try sir
$${thank}\:{you}\:{for}\:{the}\:{try}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 16/Apr/20
2) I =∫ (dx/((x+1)(√(x^2 +x+1)))) ⇒ I=∫ (dx/((x+1)(√((x+(1/2))^2 +(3/4))))) we do the changement x+(1/2) =((√3)/2) sh(t) ⇒ I =((√3)/2)∫((ch(t)dt)/((((√3)/2)sht+(1/2))((√3)/2)ch(t))) =∫ ((2dt)/(1+(√3)sh(t))) =∫((2dt)/(1+(√3)((e^t −e^(−t) )/2))) =4 ∫ (dt/(2 +(√3)e^t −(√3)e^(−t) )) =_(e^t =z) 4 ∫ (dz/(z(2+(√3)z −(√3)z^(−1) ))) =4 ∫ (dz/(2z+(√3)z^2 −(√3))) =4 ∫ (dz/( (√3)z^2 +2z−(√3))) Δ^′ =1+3 =4 ⇒z_1 =((−1+2)/( (√3))) =(1/( (√3))) and z_2 =((−1−2)/( (√3))) =−(√3) ⇒ I =4 ∫ (dz/( (√3)(z−(1/( (√3))))(z+(√3)))) =(4/( (√3)((√3)+(1/( (√3))))))∫ ((1/(z−(1/( (√3)))))−(1/(z+(√3))))dz =ln∣((z−(1/( (√3))))/(z+(√3)))∣ +C =ln∣(((√3)z−1)/( (√3)z +3))∣ +C =ln∣(((√3)e^t −1)/( (√3)e^t +3))∣ +C we have t=argsh(((2x+1)/( (√3)))) =ln(((2x+1)/( (√3)))+(√(1+(((2x+1)/( (√3))))^2 ))) ⇒ I =ln∣(((√3)(((2x+1)/( (√3) ))+(√(1+(((2x+1)/( (√3))))^2 ))−1)/( (√3)(((2x+1)/( (√3)))+(√(1+(((2x+1)/( (√3))))^2 ))+3))∣ +C
$$\left.\mathrm{2}\right)\:{I}\:=\int\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\:\Rightarrow\:{I}=\int\:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}} \\ $$$${we}\:{do}\:{the}\:{changement}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{sh}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\frac{{ch}\left({t}\right){dt}}{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sht}+\frac{\mathrm{1}}{\mathrm{2}}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)}\:=\int\:\frac{\mathrm{2}{dt}}{\mathrm{1}+\sqrt{\mathrm{3}}{sh}\left({t}\right)}\:=\int\frac{\mathrm{2}{dt}}{\mathrm{1}+\sqrt{\mathrm{3}}\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}} \\ $$$$=\mathrm{4}\:\int\:\:\frac{{dt}}{\mathrm{2}\:+\sqrt{\mathrm{3}}{e}^{{t}} −\sqrt{\mathrm{3}}{e}^{−{t}} }\:=_{{e}^{{t}} ={z}} \:\mathrm{4}\:\int\:\:\frac{{dz}}{{z}\left(\mathrm{2}+\sqrt{\mathrm{3}}{z}\:−\sqrt{\mathrm{3}}{z}^{−\mathrm{1}} \right)} \\ $$$$=\mathrm{4}\:\int\:\:\frac{{dz}}{\mathrm{2}{z}+\sqrt{\mathrm{3}}{z}^{\mathrm{2}} −\sqrt{\mathrm{3}}}\:=\mathrm{4}\:\int\:\frac{{dz}}{\:\sqrt{\mathrm{3}}{z}^{\mathrm{2}} \:+\mathrm{2}{z}−\sqrt{\mathrm{3}}} \\ $$$$\Delta^{'} =\mathrm{1}+\mathrm{3}\:=\mathrm{4}\:\Rightarrow{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\:{and}\:{z}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:=−\sqrt{\mathrm{3}}\:\Rightarrow \\ $$$${I}\:=\mathrm{4}\:\int\:\frac{{dz}}{\:\sqrt{\mathrm{3}}\left({z}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\left({z}+\sqrt{\mathrm{3}}\right)}\:=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}\int\:\left(\frac{\mathrm{1}}{{z}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}−\frac{\mathrm{1}}{{z}+\sqrt{\mathrm{3}}}\right){dz} \\ $$$$={ln}\mid\frac{{z}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{{z}+\sqrt{\mathrm{3}}}\mid\:+{C} \\ $$$$={ln}\mid\frac{\sqrt{\mathrm{3}}{z}−\mathrm{1}}{\:\sqrt{\mathrm{3}}{z}\:+\mathrm{3}}\mid\:+{C}\:={ln}\mid\frac{\sqrt{\mathrm{3}}{e}^{{t}} −\mathrm{1}}{\:\sqrt{\mathrm{3}}{e}^{{t}} \:+\mathrm{3}}\mid\:+{C}\:\:{we}\:{have}\:{t}={argsh}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$={ln}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${I}\:={ln}\mid\frac{\sqrt{\mathrm{3}}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}\:}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }−\mathrm{1}\right.}{\:\sqrt{\mathrm{3}}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }+\mathrm{3}\right.}\mid\:+{C} \\ $$
Answered by TANMAY PANACEA. last updated on 15/Apr/20
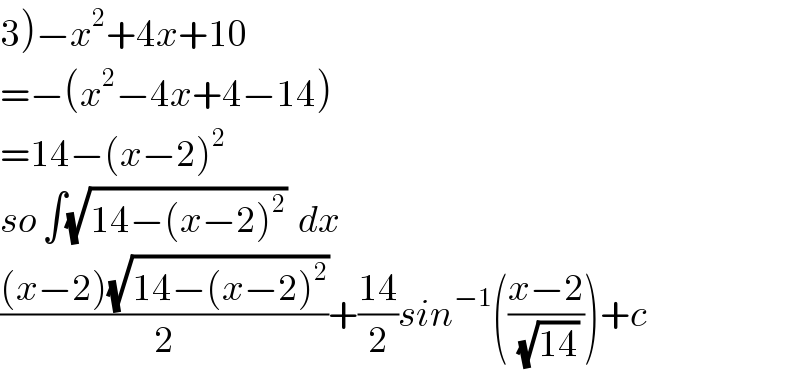
3)−x^2 +4x+10 =−(x^2 −4x+4−14) =14−(x−2)^2 so ∫(√(14−(x−2)^2 )) dx (((x−2)(√(14−(x−2)^2 )))/2)+((14)/2)sin^(−1) (((x−2)/( (√(14)))))+c
$$\left.\mathrm{3}\right)−{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{10} \\ $$$$=−\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}−\mathrm{14}\right) \\ $$$$=\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$${so}\:\int\sqrt{\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} }\:\:{dx} \\ $$$$\frac{\left({x}−\mathrm{2}\right)\sqrt{\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} }}{\mathrm{2}}+\frac{\mathrm{14}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{2}}{\:\sqrt{\mathrm{14}}}\right)+{c} \\ $$
Commented by peter frank last updated on 15/Apr/20
good
$${good} \\ $$
Commented by peter frank last updated on 15/Apr/20
good
$${good} \\ $$
Commented by TANMAY PANACEA. last updated on 15/Apr/20
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$
Commented by M±th+et£s last updated on 15/Apr/20
nice work thanx sir
$${nice}\:{work}\:{thanx}\:{sir} \\ $$
Answered by TANMAY PANACEA. last updated on 15/Apr/20
2)∫(dx/((x+1)(√(x^2 +x+1)))) x+1=(1/t) ∫((−dt)/(t^2 ×(1/t)(√(((1/t)−1)^2 +((1/t)−1)+1)))) ∫((−dt)/(t(√((1/t^2 )−(2/t)+1+(1/t))))) ∫((−tdt)/(t(√(1−2t+t^2 +t)))) ∫((−dt)/( (√(t^2 −t+1)))) ∫((−dt)/( (√(t^2 −2.t.(1/2)+(1/4)+(3/4))))) ∫((−dt)/( (√((t−(1/2))^2 +(((√3)/2))^2 )))) =(−1)[(((t−(1/2)))/2)(√((t−(1/2))^2 +(((√3)/2))^2 )) +(((((√3)/2))^2 )/2)ln{(t−(1/2))+(√((t−(1/2))^2 +(((√3)/2))^2 )) ] pls check and put t=(1/(x+1))
$$\left.\mathrm{2}\right)\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$${x}+\mathrm{1}=\frac{\mathrm{1}}{{t}} \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}}\sqrt{\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)+\mathrm{1}}} \\ $$$$\int\frac{−{dt}}{{t}\sqrt{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\mathrm{2}}{{t}}+\mathrm{1}+\frac{\mathrm{1}}{{t}}}} \\ $$$$\int\frac{−{tdt}}{{t}\sqrt{\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} +{t}}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{{t}^{\mathrm{2}} −{t}+\mathrm{1}}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{2}.{t}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}}} \\ $$$$\int\frac{−{dt}}{\:\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }} \\ $$$$=\left(−\mathrm{1}\right)\left[\frac{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:+\frac{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left\{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\right]\right. \\ $$$${pls}\:{check}\:{and}\:{put}\:{t}=\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$
Commented by TANMAY PANACEA. last updated on 15/Apr/20
most welcome
$${most}\:{welcome} \\ $$
Commented by M±th+et£s last updated on 15/Apr/20
its correct thank you sir
$${its}\:{correct}\:{thank}\:{you}\:{sir} \\ $$
Commented by peter frank last updated on 20/Apr/20
help Qn 89833(physics)
$${help}\:{Qn}\:\mathrm{89833}\left({physics}\right) \\ $$$$ \\ $$
Answered by MJS last updated on 15/Apr/20
∫x(√((x−2)/(x+1)))dx= [t=(√((x−2)/(x+1))) → dx=(2/3)(√((x−2)(x+1)))(x+1)dt] =−6∫((t^4 +2t^2 )/((t^2 −1)^3 ))dt= [Ostrogradski] =((3t(7t^2 −1))/(4(t^2 −1)^2 ))−(3/4)∫(dt/(t^2 −1))= =((3t(7t^2 −1))/(4(t^2 −1)^2 ))−(3/8)ln ((t−1)/(t+1))= =(((2x−5)(√((x−2)(x+1))))/4)−(3/8)ln ∣2x−1−2(√((x−2)(x+1)))∣ +C
$$\int{x}\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}}\:\rightarrow\:{dx}=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}\left({x}+\mathrm{1}\right){dt}\right] \\ $$$$=−\mathrm{6}\int\frac{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\frac{\mathrm{3}{t}\left(\mathrm{7}{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{4}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}= \\ $$$$=\frac{\mathrm{3}{t}\left(\mathrm{7}{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{8}}\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}= \\ $$$$=\frac{\left(\mathrm{2}{x}−\mathrm{5}\right)\sqrt{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{8}}\mathrm{ln}\:\mid\mathrm{2}{x}−\mathrm{1}−\mathrm{2}\sqrt{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}\mid\:+{C} \\ $$
Commented by M±th+et£s last updated on 15/Apr/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by TANMAY PANACEA. last updated on 15/Apr/20
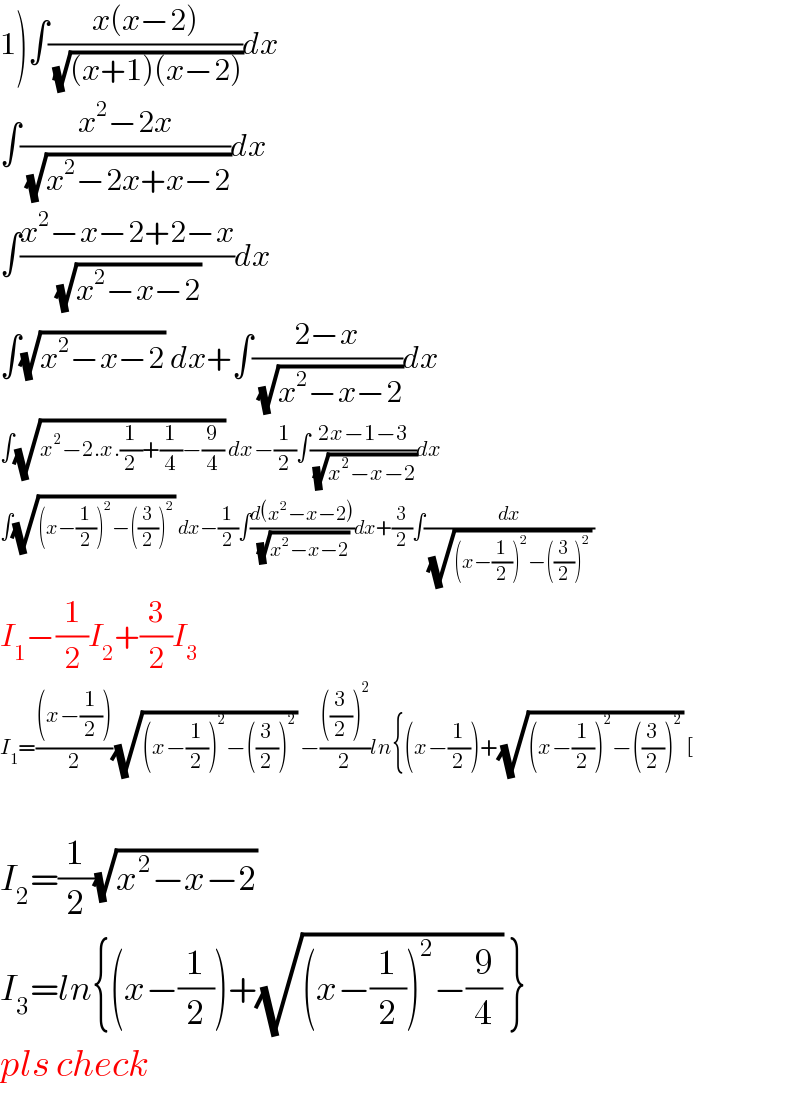
1)∫((x(x−2))/( (√((x+1)(x−2)))))dx ∫((x^2 −2x)/( (√(x^2 −2x+x−2))))dx ∫((x^2 −x−2+2−x)/( (√(x^2 −x−2))))dx ∫(√(x^2 −x−2)) dx+∫((2−x)/( (√(x^2 −x−2))))dx ∫(√(x^2 −2.x.(1/2)+(1/4)−(9/4))) dx−(1/2)∫((2x−1−3)/( (√(x^2 −x−2))))dx ∫(√((x−(1/2))^2 −((3/2))^2 )) dx−(1/2)∫((d(x^2 −x−2))/( (√(x^2 −x−2))))dx+(3/2)∫(dx/( (√((x−(1/2))^2 −((3/2))^2 )) )) I_1 −(1/2)I_2 +(3/2)I_3 I_1 =(((x−(1/2)))/2)(√((x−(1/2))^2 −((3/2))^2 )) −((((3/2))^2 )/2)ln{(x−(1/2))+(√((x−(1/2))^2 −((3/2))^2 )) [ I_2 =(1/2)(√(x^2 −x−2)) I_3 =ln{(x−(1/2))+(√((x−(1/2))^2 −(9/4))) } pls check
$$\left.\mathrm{1}\right)\int\frac{{x}\left({x}−\mathrm{2}\right)}{\:\sqrt{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}}{dx} \\ $$$$\int\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+{x}−\mathrm{2}}}{dx} \\ $$$$\int\frac{{x}^{\mathrm{2}} −{x}−\mathrm{2}+\mathrm{2}−{x}}{\:\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{2}}}{dx} \\ $$$$\int\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{2}}\:{dx}+\int\frac{\mathrm{2}−{x}}{\:\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{2}}}{dx} \\ $$$$\int\sqrt{{x}^{\mathrm{2}} −\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{4}}}\:{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{3}}{\:\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{2}}}{dx} \\ $$$$\int\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right)}{\:\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{2}}}{dx}+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }\:} \\ $$$${I}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{1}} =\frac{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }\:−\frac{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left\{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\left[\right.\right. \\ $$$$ \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −{x}−\mathrm{2}}\: \\ $$$${I}_{\mathrm{3}} ={ln}\left\{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}}\:\right\} \\ $$$${pls}\:{check} \\ $$
Commented by M±th+et£s last updated on 15/Apr/20
thank you verry much
$${thank}\:{you}\:{verry}\:{much} \\ $$
Commented by TANMAY PANACEA. last updated on 15/Apr/20
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$
Answered by MJS last updated on 15/Apr/20
∫(dx/((x+1)(√(x^2 +x+1))))= [t=2x+1 → dx=(dt/2)] =2∫(dt/((t+1)(√(t^2 +3))))= [u=((√3)/3)(t+(√(t^2 +3))) → dt=((√(3(t^2 +3)))/(t+(√(t^2 +3))))du] =((4(√3))/3)∫(du/(u^2 +((2(√3))/3)u−1))= =∫(du/(u−((√3)/3)))−∫(du/(u+(√3)))=ln (u−((√3)/3)) −ln (u+(√3)) = =ln ((u−((√3)/3))/(u+(√3))) =...=ln ((t−3+2(√(t^2 +3)))/(t+1)) = =ln ((x−1+2(√(x^2 +x+1)))/(x+1)) +C
$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}{x}+\mathrm{1}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}\right)\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{3}\right)}}{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{du}\right] \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}{u}−\mathrm{1}}= \\ $$$$=\int\frac{{du}}{{u}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}−\int\frac{{du}}{{u}+\sqrt{\mathrm{3}}}=\mathrm{ln}\:\left({u}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\:−\mathrm{ln}\:\left({u}+\sqrt{\mathrm{3}}\right)\:= \\ $$$$=\mathrm{ln}\:\frac{{u}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}{{u}+\sqrt{\mathrm{3}}}\:=…=\mathrm{ln}\:\frac{{t}−\mathrm{3}+\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{{t}+\mathrm{1}}\:= \\ $$$$=\mathrm{ln}\:\frac{{x}−\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}+\mathrm{1}}\:+{C} \\ $$
Answered by 242242864 last updated on 16/Apr/20
3) ∫(√(−x^2 +4x+10 )) dx consider −x^2 +4x+10 =−[x^2 −4x−10] −[(x−2)^2 −10−4] −[(x−2)^2 −14] 14−(x−2)^2 ⇒∫(√(−x+4x+10)) = ∫(√(14−(x−2)^2 )) let (√(14−(x−2)^2 )) =(√(a^2 (1−sin^2 𝛉))) 14−(x−2)^2 = a^2 (1−sin^2 𝛉) 14−(x−2)^2 = a^2 −a^2 sin^2 𝛉 ⇒a^2 = 14 (x−2)^2 =14sin^2 θ (x−2)=(√(14))sin θ sin θ= (((x−2))/( (√(14)))) θ= sin^(−1 ) (((x−2))/( (√(14)))) from (x−2)= (√(14))sin θ dx=(√(14))cos θdθ ∫(√(14(1−sin^2 θ))) .(((√(14))cos θdθ)/1) ∫dθ = θ+C =sin^(−1) (((x−2))/( (√(14))))+C something missing?
$$ \\ $$$$ \\ $$$$\left.\mathrm{3}\right)\:\:\int\sqrt{−{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{10}\:}\:{dx} \\ $$$${consider}\:−{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{10} \\ $$$$=−\left[{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{10}\right] \\ $$$$−\left[\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{10}−\mathrm{4}\right] \\ $$$$−\left[\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{14}\right] \\ $$$$\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\int\sqrt{−{x}+\mathrm{4}{x}+\mathrm{10}}\:=\:\int\sqrt{\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\boldsymbol{{let}}\:\sqrt{\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} }\:=\sqrt{\boldsymbol{{a}}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\theta}\right)} \\ $$$$\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\:\boldsymbol{{a}}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\theta}\right) \\ $$$$ \\ $$$$\mathrm{14}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} \:=\:\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\theta} \\ $$$$\Rightarrow\boldsymbol{{a}}^{\mathrm{2}} \:=\:\mathrm{14} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{14sin}\:^{\mathrm{2}} \theta \\ $$$$\left({x}−\mathrm{2}\right)=\sqrt{\mathrm{14}}\mathrm{sin}\:\theta \\ $$$$\mathrm{sin}\:\theta=\:\frac{\left({x}−\mathrm{2}\right)}{\:\sqrt{\mathrm{14}}} \\ $$$$\theta=\:\mathrm{sin}\:^{−\mathrm{1}\:} \frac{\left({x}−\mathrm{2}\right)}{\:\sqrt{\mathrm{14}}} \\ $$$${from}\:\left({x}−\mathrm{2}\right)=\:\sqrt{\mathrm{14}}\mathrm{sin}\:\theta \\ $$$${dx}=\sqrt{\mathrm{14}}\mathrm{cos}\:\theta{d}\theta \\ $$$$\int\sqrt{\mathrm{14}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta\right)}\:.\frac{\sqrt{\mathrm{14}}\mathrm{cos}\:\theta{d}\theta}{\mathrm{1}} \\ $$$$\int{d}\theta\:=\:\theta+{C} \\ $$$$=\mathrm{sin}\:^{−\mathrm{1}} \:\frac{\left({x}−\mathrm{2}\right)}{\:\sqrt{\mathrm{14}}}+{C} \\ $$$$ \\ $$$${something}\:{missing}? \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *