Question Number 55992 by Mikael_Marshall last updated on 07/Mar/19
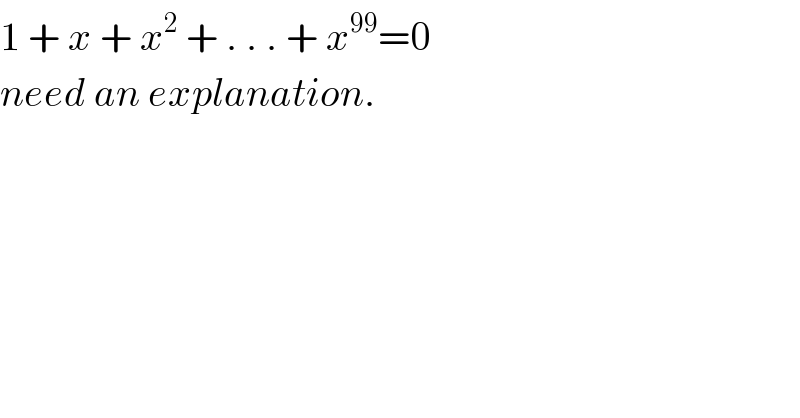
$$\mathrm{1}\:+\:{x}\:+\:{x}^{\mathrm{2}} \:+\:.\:.\:.\:+\:{x}^{\mathrm{99}} =\mathrm{0} \\ $$$${need}\:{an}\:{explanation}. \\ $$
Commented by mr W last updated on 07/Mar/19
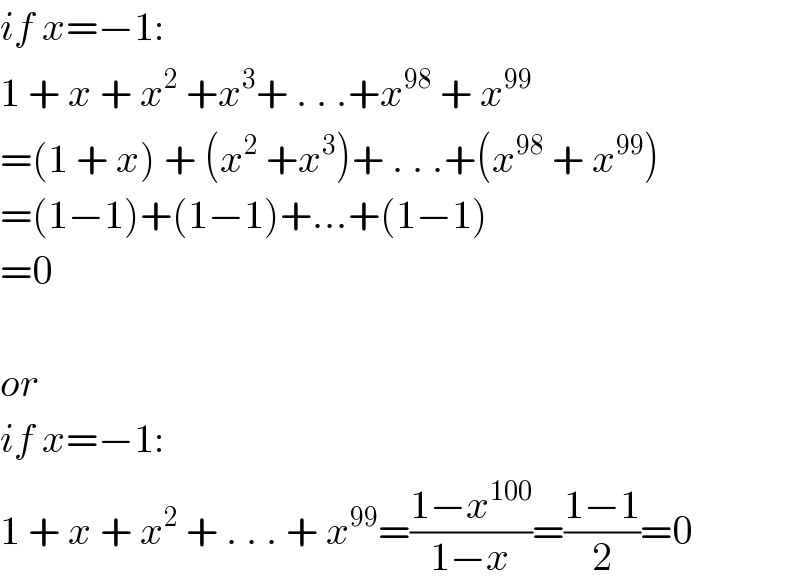
$${if}\:{x}=−\mathrm{1}: \\ $$$$\mathrm{1}\:+\:{x}\:+\:{x}^{\mathrm{2}} \:+{x}^{\mathrm{3}} +\:.\:.\:.+{x}^{\mathrm{98}} \:+\:{x}^{\mathrm{99}} \\ $$$$=\left(\mathrm{1}\:+\:{x}\right)\:+\:\left({x}^{\mathrm{2}} \:+{x}^{\mathrm{3}} \right)+\:.\:.\:.+\left({x}^{\mathrm{98}} \:+\:{x}^{\mathrm{99}} \right) \\ $$$$=\left(\mathrm{1}−\mathrm{1}\right)+\left(\mathrm{1}−\mathrm{1}\right)+…+\left(\mathrm{1}−\mathrm{1}\right) \\ $$$$=\mathrm{0} \\ $$$$ \\ $$$${or} \\ $$$${if}\:{x}=−\mathrm{1}: \\ $$$$\mathrm{1}\:+\:{x}\:+\:{x}^{\mathrm{2}} \:+\:.\:.\:.\:+\:{x}^{\mathrm{99}} =\frac{\mathrm{1}−{x}^{\mathrm{100}} }{\mathrm{1}−{x}}=\frac{\mathrm{1}−\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$
Commented by maxmathsup by imad last updated on 07/Mar/19
![if x from C (e) ⇔ ((1−x^(100) )/(1−x)) =0 with x≠1 ⇒x^(100) =1 =e^(i2kπ) ⇒ x_k =e^((ikπ)/(50)) and k∈[[1,99]] are roots of this equation.](https://www.tinkutara.com/question/Q56002.png)
$${if}\:{x}\:{from}\:{C}\:\:\:\left({e}\right)\:\Leftrightarrow\:\frac{\mathrm{1}−{x}^{\mathrm{100}} }{\mathrm{1}−{x}}\:=\mathrm{0}\:\:{with}\:{x}\neq\mathrm{1}\:\Rightarrow{x}^{\mathrm{100}} =\mathrm{1}\:={e}^{{i}\mathrm{2}{k}\pi} \:\Rightarrow \\ $$$${x}_{{k}} ={e}^{\frac{{ik}\pi}{\mathrm{50}}} \:\:\:\:\:\:{and}\:{k}\in\left[\left[\mathrm{1},\mathrm{99}\right]\right]\:\:{are}\:{roots}\:{of}\:\:{this}\:{equation}. \\ $$
