1-x-x-dx-

Question Number 36997 by rahul 19 last updated on 07/Jun/18

$$\int\:\sqrt{\frac{\mathrm{1}+{x}}{{x}}\:}{dx}\:=\:? \\ $$

Commented by behi83417@gmail.com last updated on 07/Jun/18

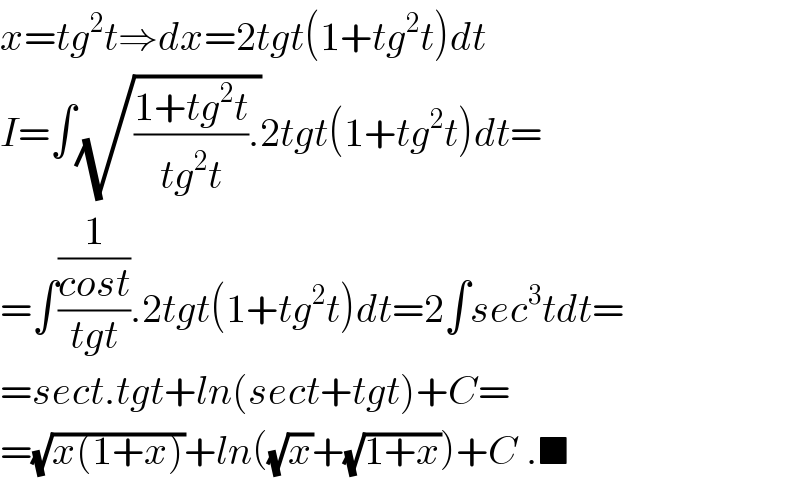
x=tg^2 t⇒dx=2tgt(1+tg^2 t)dt I=∫(√(((1+tg^2 t)/(tg^2 t)).))2tgt(1+tg^2 t)dt= =∫((1/(cost))/(tgt)).2tgt(1+tg^2 t)dt=2∫sec^3 tdt= =sect.tgt+ln(sect+tgt)+C= =(√(x(1+x)))+ln((√x)+(√(1+x)))+C .■

$${x}={tg}^{\mathrm{2}} {t}\Rightarrow{dx}=\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt} \\ $$$${I}=\int\sqrt{\frac{\mathrm{1}+{tg}^{\mathrm{2}} {t}}{{tg}^{\mathrm{2}} {t}}.}\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt}= \\ $$$$=\int\frac{\frac{\mathrm{1}}{{cost}}}{{tgt}}.\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt}=\mathrm{2}\int{sec}^{\mathrm{3}} {tdt}= \\ $$$$={sect}.{tgt}+{ln}\left({sect}+{tgt}\right)+{C}= \\ $$$$=\sqrt{{x}\left(\mathrm{1}+{x}\right)}+{ln}\left(\sqrt{{x}}+\sqrt{\mathrm{1}+{x}}\right)+{C}\:.\blacksquare \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jun/18

∫((1+x)/( (√(x+x^2 ))))dx (1/2)∫((1+1+2x)/( (√(x+x^2 ))))dx =(1/2)∫(dx/( (√(x^2 +2.x.(1/2)+(1/4)−(1/4)))))+(1/2)∫((d(x+x^2 ))/( (√(x+x^2 )))) =(1/2)∫(dx/( (√((x+(1/2))^2 −((1/2))^2 )))) +(1/2)×(((x+x^2 )^(1/2) )/(1/2)) use formula ∫(dx/( (√(X^2 −A^2 ))))

$$\int\frac{\mathrm{1}+{x}}{\:\sqrt{{x}+{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\mathrm{1}+\mathrm{2}{x}}{\:\sqrt{{x}+{x}^{\mathrm{2}} }}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}.{x}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+{x}^{\mathrm{2}} \right)}{\:\sqrt{{x}+{x}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }}\:+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left({x}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${use}\:{formula}\:\int\frac{{dx}}{\:\sqrt{{X}^{\mathrm{2}} −{A}^{\mathrm{2}} }} \\ $$

Answered by MJS last updated on 07/Jun/18

∫(√((1+x)/x))dx=∫((√(1+x))/( (√x)))dx= [t=(√x) → dx=2(√x)dt] =2∫(√(1+t^2 ))= [u=arctan t → dt=sec^2 u du] =2∫sec^2 u (√(1+tan^2 u)) du=2∫sec^3 u du= [∫sec^n u du=((sec^(n−2) u tan u)/(n−1))+((n−2)/(n−1))∫sec^(n−2) u du] =sec u tan u +∫sec u du= =sec u tan u +ln(sec u +tan u)= =t(√(1+t^2 ))+ln((√(1+t^2 ))+t)= =(√(x(1+x)))+ln((√(1+x))+(√x))+C

$$\int\sqrt{\frac{\mathrm{1}+{x}}{{x}}}{dx}=\int\frac{\sqrt{\mathrm{1}+{x}}}{\:\sqrt{{x}}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}{dt}\right] \\ $$$$=\mathrm{2}\int\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\mathrm{arctan}\:{t}\:\rightarrow\:{dt}=\mathrm{sec}^{\mathrm{2}} \:{u}\:{du}\right] \\ $$$$=\mathrm{2}\int\mathrm{sec}^{\mathrm{2}} \:{u}\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{u}}\:{du}=\mathrm{2}\int\mathrm{sec}^{\mathrm{3}} \:{u}\:{du}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\int\mathrm{sec}^{{n}} \:{u}\:{du}=\frac{\mathrm{sec}^{{n}−\mathrm{2}} \:{u}\:\mathrm{tan}\:{u}}{{n}−\mathrm{1}}+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{sec}^{{n}−\mathrm{2}} \:{u}\:{du}\right] \\ $$$$=\mathrm{sec}\:{u}\:\mathrm{tan}\:{u}\:+\int\mathrm{sec}\:{u}\:{du}= \\ $$$$=\mathrm{sec}\:{u}\:\mathrm{tan}\:{u}\:+\mathrm{ln}\left(\mathrm{sec}\:{u}\:+\mathrm{tan}\:{u}\right)= \\ $$$$={t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{ln}\left(\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+{t}\right)= \\ $$$$=\sqrt{{x}\left(\mathrm{1}+{x}\right)}+\mathrm{ln}\left(\sqrt{\mathrm{1}+{x}}+\sqrt{{x}}\right)+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply