1-x-y-2-x-1-y-3-find-x-2-y-2-

Question Number 91843 by jagoll last updated on 03/May/20

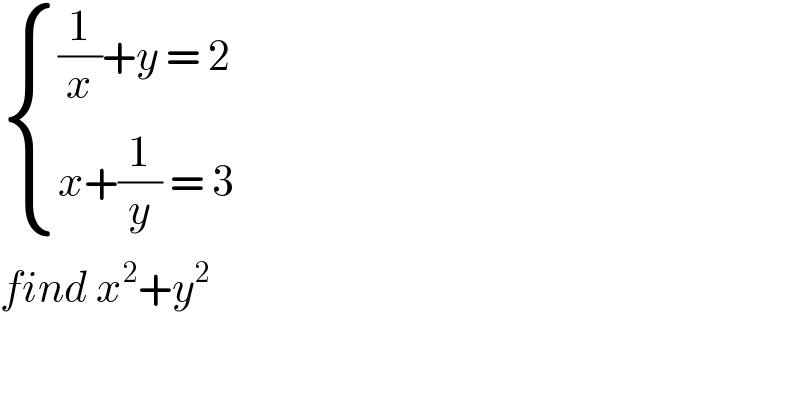
$$\begin{cases}{\frac{\mathrm{1}}{{x}}+{y}\:=\:\mathrm{2}}\\{{x}+\frac{\mathrm{1}}{{y}}\:=\:\mathrm{3}}\end{cases} \\ $$$${find}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$

Commented by jagoll last updated on 03/May/20

Commented by jagoll last updated on 03/May/20

��

Commented by john santu last updated on 03/May/20

��

Commented by Prithwish Sen 1 last updated on 03/May/20

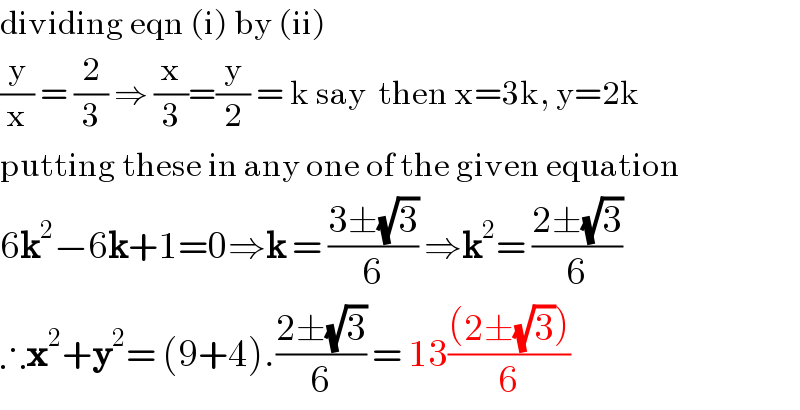
dividing eqn (i) by (ii) (y/x) = (2/3) ⇒ (x/3)=(y/2) = k say then x=3k, y=2k putting these in any one of the given equation 6k^2 −6k+1=0⇒k = ((3±(√3))/6) ⇒k^2 = ((2±(√3))/6) ∴x^2 +y^2 = (9+4).((2±(√3))/6) = 13(((2±(√3)))/6)

$$\mathrm{dividing}\:\mathrm{eqn}\:\left(\mathrm{i}\right)\:\mathrm{by}\:\left(\mathrm{ii}\right) \\ $$$$\frac{\mathrm{y}}{\mathrm{x}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\:\frac{\mathrm{x}}{\mathrm{3}}=\frac{\mathrm{y}}{\mathrm{2}}\:=\:\mathrm{k}\:\mathrm{say}\:\:\mathrm{then}\:\mathrm{x}=\mathrm{3k},\:\mathrm{y}=\mathrm{2k} \\ $$$$\mathrm{putting}\:\mathrm{these}\:\mathrm{in}\:\mathrm{any}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\mathrm{6}\boldsymbol{\mathrm{k}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{\mathrm{k}}+\mathrm{1}=\mathrm{0}\Rightarrow\boldsymbol{\mathrm{k}}\:=\:\frac{\mathrm{3}\pm\sqrt{\mathrm{3}}}{\mathrm{6}}\:\Rightarrow\boldsymbol{\mathrm{k}}^{\mathrm{2}} =\:\frac{\mathrm{2}\pm\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$$$\therefore\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\:\left(\mathrm{9}+\mathrm{4}\right).\frac{\mathrm{2}\pm\sqrt{\mathrm{3}}}{\mathrm{6}}\:=\:\mathrm{13}\frac{\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right)}{\mathrm{6}} \\ $$

Commented by jagoll last updated on 03/May/20

��✒️

Answered by mr W last updated on 03/May/20

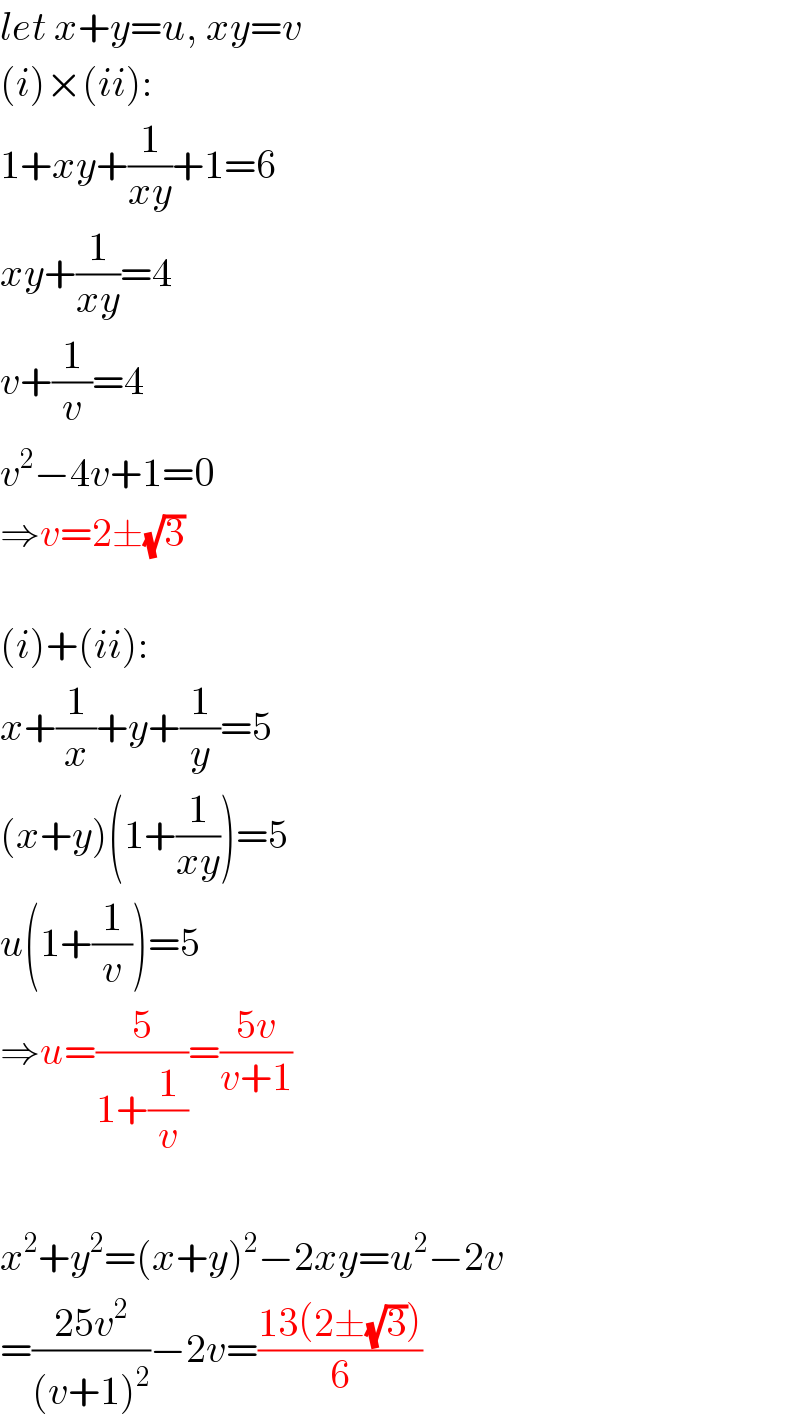
let x+y=u, xy=v (i)×(ii): 1+xy+(1/(xy))+1=6 xy+(1/(xy))=4 v+(1/v)=4 v^2 −4v+1=0 ⇒v=2±(√3) (i)+(ii): x+(1/x)+y+(1/y)=5 (x+y)(1+(1/(xy)))=5 u(1+(1/v))=5 ⇒u=(5/(1+(1/v)))=((5v)/(v+1)) x^2 +y^2 =(x+y)^2 −2xy=u^2 −2v =((25v^2 )/((v+1)^2 ))−2v=((13(2±(√3)))/6)

$${let}\:{x}+{y}={u},\:{xy}={v} \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\mathrm{1}+{xy}+\frac{\mathrm{1}}{{xy}}+\mathrm{1}=\mathrm{6} \\ $$$${xy}+\frac{\mathrm{1}}{{xy}}=\mathrm{4} \\ $$$${v}+\frac{\mathrm{1}}{{v}}=\mathrm{4} \\ $$$${v}^{\mathrm{2}} −\mathrm{4}{v}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{v}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${x}+\frac{\mathrm{1}}{{x}}+{y}+\frac{\mathrm{1}}{{y}}=\mathrm{5} \\ $$$$\left({x}+{y}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{xy}}\right)=\mathrm{5} \\ $$$${u}\left(\mathrm{1}+\frac{\mathrm{1}}{{v}}\right)=\mathrm{5} \\ $$$$\Rightarrow{u}=\frac{\mathrm{5}}{\mathrm{1}+\frac{\mathrm{1}}{{v}}}=\frac{\mathrm{5}{v}}{{v}+\mathrm{1}} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}={u}^{\mathrm{2}} −\mathrm{2}{v} \\ $$$$=\frac{\mathrm{25}{v}^{\mathrm{2}} }{\left({v}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{2}{v}=\frac{\mathrm{13}\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\right)}{\mathrm{6}} \\ $$

Commented by jagoll last updated on 03/May/20

��

Answered by MJS last updated on 03/May/20

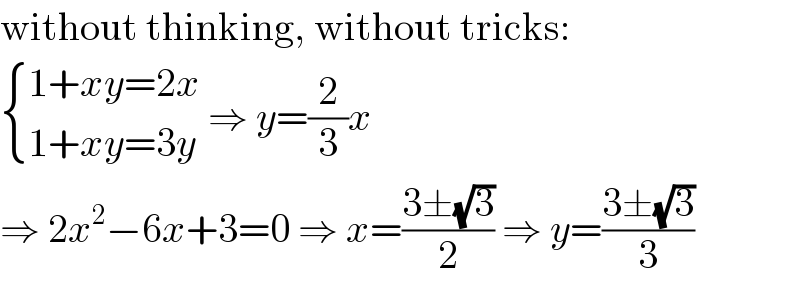
without thinking, without tricks: { ((1+xy=2x)),((1+xy=3y)) :} ⇒ y=(2/3)x ⇒ 2x^2 −6x+3=0 ⇒ x=((3±(√3))/2) ⇒ y=((3±(√3))/3)

$$\mathrm{without}\:\mathrm{thinking},\:\mathrm{without}\:\mathrm{tricks}: \\ $$$$\begin{cases}{\mathrm{1}+{xy}=\mathrm{2}{x}}\\{\mathrm{1}+{xy}=\mathrm{3}{y}}\end{cases}\:\Rightarrow\:{y}=\frac{\mathrm{2}}{\mathrm{3}}{x} \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{3}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{3}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\:{y}=\frac{\mathrm{3}\pm\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$

Commented by jagoll last updated on 03/May/20

��

Commented by Ar Brandon last updated on 03/May/20

�� Brilliant !

Facebook Tweet Pin

1-x-y-2-x-1-y-3-find-x-2-y-2-

Leave a Reply Cancel reply