Question Number 126229 by MathSh last updated on 18/Dec/20

$$\left(\mathrm{1}+{y}\right){x}'={x} \\ $$
Answered by Dwaipayan Shikari last updated on 18/Dec/20
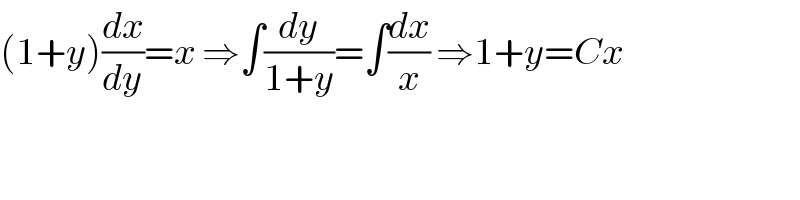
$$\left(\mathrm{1}+{y}\right)\frac{{dx}}{{dy}}={x}\:\Rightarrow\int\frac{{dy}}{\mathrm{1}+{y}}=\int\frac{{dx}}{{x}}\:\Rightarrow\mathrm{1}+{y}={Cx} \\ $$
Answered by ebi last updated on 18/Dec/20
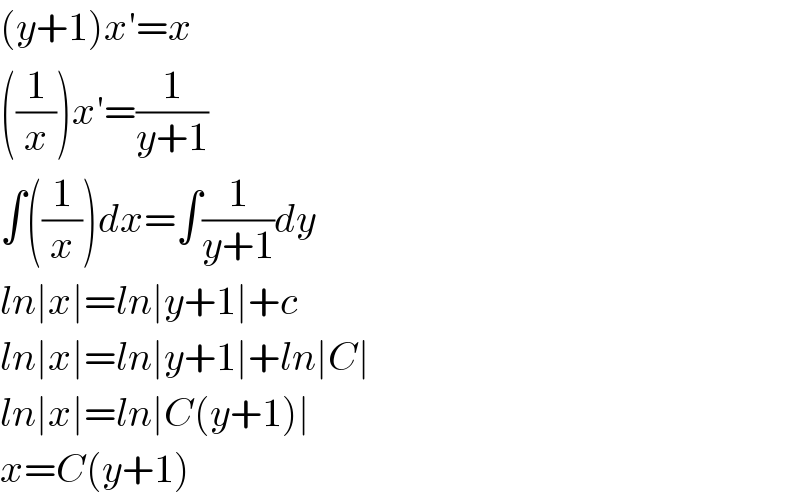
$$\left({y}+\mathrm{1}\right){x}'={x} \\ $$$$\left(\frac{\mathrm{1}}{{x}}\right){x}'=\frac{\mathrm{1}}{{y}+\mathrm{1}} \\ $$$$\int\left(\frac{\mathrm{1}}{{x}}\right){dx}=\int\frac{\mathrm{1}}{{y}+\mathrm{1}}{dy} \\ $$$${ln}\mid{x}\mid={ln}\mid{y}+\mathrm{1}\mid+{c} \\ $$$${ln}\mid{x}\mid={ln}\mid{y}+\mathrm{1}\mid+{ln}\mid{C}\mid \\ $$$${ln}\mid{x}\mid={ln}\mid{C}\left({y}+\mathrm{1}\right)\mid \\ $$$${x}={C}\left({y}+\mathrm{1}\right) \\ $$
