Question Number 183059 by Shrinava last updated on 19/Dec/22
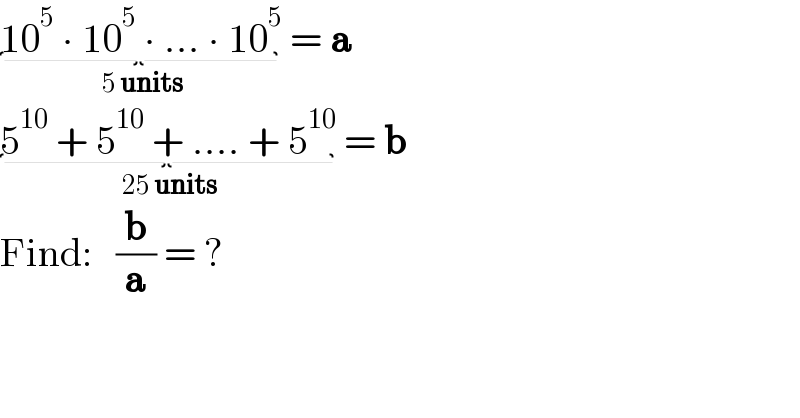
$$\underset{\:\mathrm{5}\:\boldsymbol{\mathrm{units}}} {\underbrace{\mathrm{10}^{\mathrm{5}} \:\centerdot\:\mathrm{10}^{\mathrm{5}} \:\centerdot\:…\:\centerdot\:\mathrm{10}^{\mathrm{5}} }}\:=\:\boldsymbol{\mathrm{a}} \\ $$$$\underset{\:\mathrm{25}\:\boldsymbol{\mathrm{units}}} {\underbrace{\mathrm{5}^{\mathrm{10}} \:+\:\mathrm{5}^{\mathrm{10}} \:+\:….\:+\:\mathrm{5}^{\mathrm{10}} }}\:=\:\boldsymbol{\mathrm{b}} \\ $$$$\mathrm{Find}:\:\:\:\frac{\boldsymbol{\mathrm{b}}}{\boldsymbol{\mathrm{a}}}\:=\:? \\ $$
Commented by Jeduardo7 last updated on 19/Dec/22
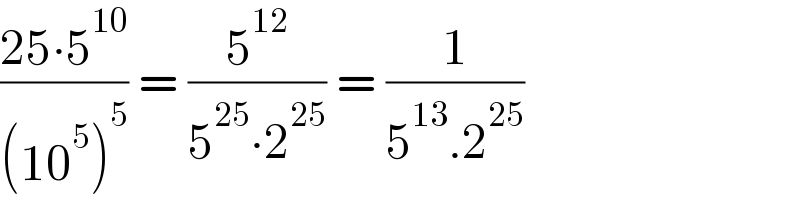
$$\frac{\mathrm{25}\centerdot\mathrm{5}^{\mathrm{10}} }{\left(\mathrm{10}^{\mathrm{5}} \right)^{\mathrm{5}} }\:=\:\frac{\mathrm{5}^{\mathrm{12}} }{\mathrm{5}^{\mathrm{25}} \centerdot\mathrm{2}^{\mathrm{25}} }\:=\:\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{13}} .\mathrm{2}^{\mathrm{25}} } \\ $$
