Question Number 103406 by mr W last updated on 16/Jul/20

$$\mathrm{100}\:{students}\:{are}\:{standing}\:{in}\:{a}\:{row}. \\ $$$$\mathrm{4}\:{students}\:{should}\:{be}\:{selected}\:{in}\:{the} \\ $$$${way}\:{that}\:{no}\:{two}\:{of}\:{them}\:{are}\:{next}\:{to} \\ $$$${each}\:{other}.\:{how}\:{many}\:{ways}\:{do}\:{you} \\ $$$${have}\:{to}\:{do}\:{this}? \\ $$
Commented by bobhans last updated on 15/Jul/20
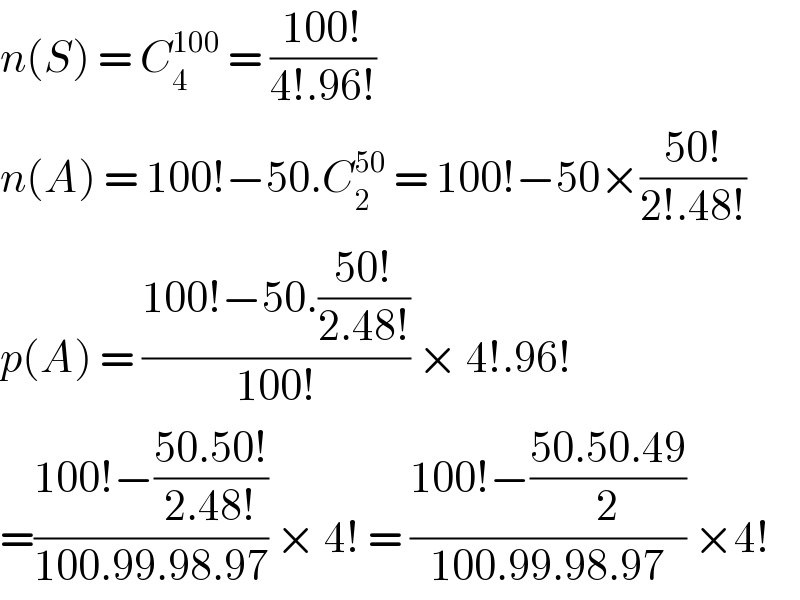
$${n}\left({S}\right)\:=\:{C}_{\mathrm{4}} ^{\mathrm{100}} \:=\:\frac{\mathrm{100}!}{\mathrm{4}!.\mathrm{96}!} \\ $$$${n}\left({A}\right)\:=\:\mathrm{100}!−\mathrm{50}.{C}_{\mathrm{2}} ^{\mathrm{50}} \:=\:\mathrm{100}!−\mathrm{50}×\frac{\mathrm{50}!}{\mathrm{2}!.\mathrm{48}!} \\ $$$${p}\left({A}\right)\:=\:\frac{\mathrm{100}!−\mathrm{50}.\frac{\mathrm{50}!}{\mathrm{2}.\mathrm{48}!}}{\mathrm{100}!}\:×\:\mathrm{4}!.\mathrm{96}! \\ $$$$=\frac{\mathrm{100}!−\frac{\mathrm{50}.\mathrm{50}!}{\mathrm{2}.\mathrm{48}!}}{\mathrm{100}.\mathrm{99}.\mathrm{98}.\mathrm{97}}\:×\:\mathrm{4}!\:=\:\frac{\mathrm{100}!−\frac{\mathrm{50}.\mathrm{50}.\mathrm{49}}{\mathrm{2}}}{\mathrm{100}.\mathrm{99}.\mathrm{98}.\mathrm{97}}\:×\mathrm{4}! \\ $$
Commented by mr W last updated on 16/Jul/20

$$\mathrm{3}\:\mathrm{464}\:\mathrm{840}\:{ways} \\ $$
Commented by mr W last updated on 16/Jul/20

$${answer}\:{see}\:{Q}\mathrm{103716} \\ $$
