Question Number 25387 by mubeen897@hotmail.com last updated on 09/Dec/17
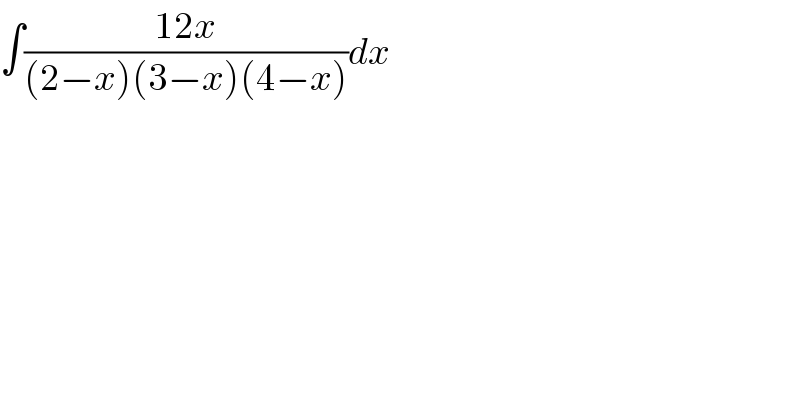
$$\int\frac{\mathrm{12}{x}}{\left(\mathrm{2}−{x}\right)\left(\mathrm{3}−{x}\right)\left(\mathrm{4}−{x}\right)}{dx} \\ $$$$ \\ $$
Answered by A1B1C1D1 last updated on 09/Dec/17

$$\mathrm{Problem}: \\ $$$$ \\ $$$$\int\:\:\frac{\mathrm{12x}}{\left(\mathrm{2}\:−\:\mathrm{x}\right)\left(\mathrm{3}\:−\:\mathrm{x}\right)\left(\mathrm{4}\:−\:\mathrm{x}\right)}\:\mathrm{dx} \\ $$$$ \\ $$$$\mathrm{Rewrite}/\mathrm{simplify}: \\ $$$$ \\ $$$$\int\:−\:\frac{\mathrm{12x}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)\left(\mathrm{x}\:−\:\mathrm{3}\right)\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:\mathrm{dx} \\ $$$$−\mathrm{12}\:\int\:\frac{\mathrm{x}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)\left(\mathrm{x}\:−\:\mathrm{3}\right)\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:\mathrm{dx}\: \\ $$$$ \\ $$$$\mathrm{Now}\:\mathrm{solving}: \\ $$$$\:\int\:\frac{\mathrm{x}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)\left(\mathrm{x}\:−\:\mathrm{3}\right)\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:\mathrm{dx} \\ $$$$\mathrm{Perform}\:\mathrm{partial}\:\mathrm{fraction}\:\mathrm{decomposition}: \\ $$$$\int\:\left(\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:−\:\frac{\mathrm{3}}{\left(\mathrm{x}\:−\:\mathrm{3}\right)}\:+\:\frac{\mathrm{2}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)}\right)\:\mathrm{dx} \\ $$$$\mathrm{Apply}\:\mathrm{linearity}: \\ $$$$\int\:\frac{\mathrm{1}}{\left(\mathrm{x}−\:\mathrm{2}\right)}\:\mathrm{dx}\:−\:\mathrm{3}\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{3}\right)}\:\mathrm{dx}\:+\:\mathrm{2}\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)}\:\mathrm{dx} \\ $$$$\mathrm{Now}\:\mathrm{solving}: \\ $$$$\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:\mathrm{dx} \\ $$$$\mathrm{Substitute}\:\mathrm{u}\:=\:\mathrm{x}\:−\:\mathrm{2}\:=>\:\mathrm{du}\:=\:\mathrm{dx}: \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{u}}\:\mathrm{du}\: \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{a}\:\mathrm{standard}\:\mathrm{integral}: \\ $$$$\mathrm{ln}\left(\mathrm{u}\right) \\ $$$$\mathrm{Undo}\:\mathrm{substituition}\:\mathrm{u}\:=\:\mathrm{x}\:−\:\mathrm{2}: \\ $$$$\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{2}\right) \\ $$$$\mathrm{Now}\:\mathrm{solving}: \\ $$$$\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{3}\right)}\:\mathrm{dx} \\ $$$$\mathrm{Substitute}\:\mathrm{u}\:=\:\mathrm{x}\:−\:\mathrm{3}\:=>\:\mathrm{du}\:=\:\mathrm{dx}: \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{u}}\:\mathrm{du} \\ $$$$\mathrm{Use}\:\mathrm{previous}\:\mathrm{result}: \\ $$$$\mathrm{ln}\left(\mathrm{u}\right) \\ $$$$\mathrm{Undo}\:\mathrm{substituition}\:\mathrm{u}\:=\:\mathrm{x}\:−\:\mathrm{3}: \\ $$$$\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{3}\right) \\ $$$$\mathrm{Now}\:\mathrm{solving}: \\ $$$$\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)}\:\mathrm{dx} \\ $$$$\mathrm{Substitute}\:\mathrm{u}\:=\:\mathrm{x}\:−\:\mathrm{4}\:=>\:\mathrm{du}\:=\:\mathrm{dx}: \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{u}}\:\mathrm{du} \\ $$$$\mathrm{Use}\:\mathrm{previous}\:\mathrm{result}: \\ $$$$\mathrm{ln}\left(\mathrm{u}\right) \\ $$$$\mathrm{Undo}\:\mathrm{substituition}\:\mathrm{u}\:=\:\mathrm{x}\:−\:\mathrm{4}: \\ $$$$\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{4}\right) \\ $$$$\mathrm{Plug}\:\mathrm{in}\:\mathrm{solved}\:\mathrm{integrals}: \\ $$$$\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:\mathrm{dx}\:−\:\mathrm{3}\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\:\mathrm{3}\right)}\:\mathrm{dx}\:+\:\mathrm{2}\int\:\frac{\mathrm{1}}{\left(\mathrm{x}\:−\mathrm{4}\right)}\:\mathrm{dx} \\ $$$$ \\ $$$$\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{2}\right)\:−\:\mathrm{3}\:\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{3}\right)\:+\:\mathrm{2}\:\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{4}\right) \\ $$$$\mathrm{Plug}\:\mathrm{in}\:\mathrm{solved}\:\mathrm{integrals}: \\ $$$$−\:\mathrm{12}\int\:\frac{\mathrm{x}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)\left(\mathrm{x}\:−\:\mathrm{3}\right)\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:\mathrm{dx} \\ $$$$ \\ $$$$−\:\mathrm{12}\:\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{2}\right)\:+\:\mathrm{36}\:\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{3}\right)\:−\:\mathrm{24}\:\mathrm{ln}\left(\mathrm{x}\:−\:\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{problem}\:\mathrm{is}\:\mathrm{solved}.\:\mathrm{Apply}\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{value}\:\mathrm{function}\:\mathrm{to}\:\mathrm{arguments}\:\mathrm{of}\:\mathrm{logarithm}\:\mathrm{functions}\:\mathrm{in}\:\mathrm{order}\:\mathrm{to}\:\mathrm{extend}\:\mathrm{the}\:\mathrm{antiderivative}'\mathrm{s}\:\mathrm{domain}: \\ $$$$\int\:−\:\frac{\mathrm{12x}}{\left(\mathrm{x}\:−\:\mathrm{4}\right)\left(\mathrm{x}\:−\:\mathrm{3}\right)\left(\mathrm{x}\:−\:\mathrm{2}\right)}\:\mathrm{dx} \\ $$$$ \\ $$$$−\mathrm{12}\:\mathrm{ln}\left(\mid\mathrm{x}−\mathrm{2}\mid\right)\:+\:\mathrm{36}\:\mathrm{ln}\left(\mid\mathrm{x}\:−\:\mathrm{3}\mid\right)\:−\:\mathrm{24}\:\mathrm{ln}\left(\mid\mathrm{x}\:−\:\mathrm{4}\mid\right)\:+\:\mathrm{C} \\ $$
