Question Number 60337 by arcana last updated on 20/May/19

$$\mathrm{15},\mathrm{25},\mathrm{42},…? \\ $$
Commented by MJS last updated on 20/May/19
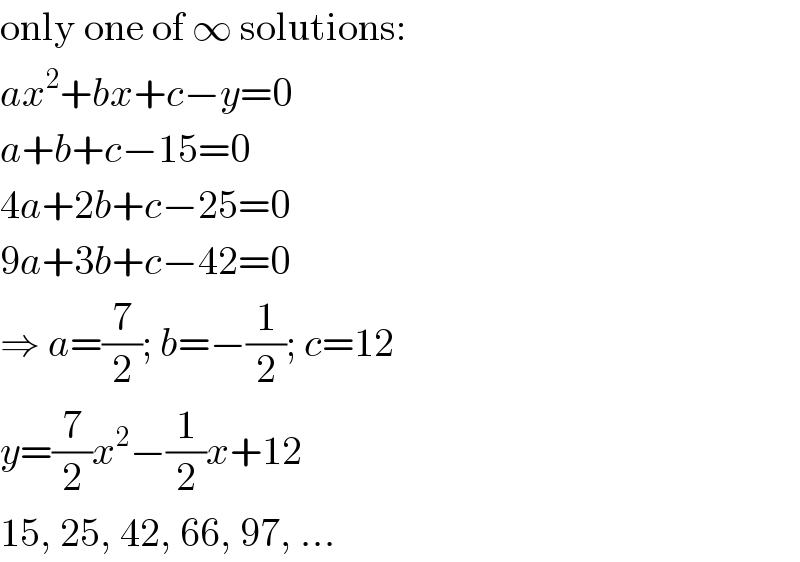
$$\mathrm{only}\:\mathrm{one}\:\mathrm{of}\:\infty\:\mathrm{solutions}: \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}−{y}=\mathrm{0} \\ $$$${a}+{b}+{c}−\mathrm{15}=\mathrm{0} \\ $$$$\mathrm{4}{a}+\mathrm{2}{b}+{c}−\mathrm{25}=\mathrm{0} \\ $$$$\mathrm{9}{a}+\mathrm{3}{b}+{c}−\mathrm{42}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=\frac{\mathrm{7}}{\mathrm{2}};\:{b}=−\frac{\mathrm{1}}{\mathrm{2}};\:{c}=\mathrm{12} \\ $$$${y}=\frac{\mathrm{7}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{12} \\ $$$$\mathrm{15},\:\mathrm{25},\:\mathrm{42},\:\mathrm{66},\:\mathrm{97},\:… \\ $$
Commented by arcana last updated on 20/May/19

$$\mathrm{graciaaas}.\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{method}\:\mathrm{name}'\mathrm{s}? \\ $$
