Question Number 27213 by shiv15031973@gmail.com last updated on 04/Jan/18
![[(16x^4 −1)]/[2x−1] factorise it](https://www.tinkutara.com/question/Q27213.png)
$$\left[\left(\mathrm{16}{x}^{\mathrm{4}} −\mathrm{1}\right)\right]/\left[\mathrm{2}{x}−\mathrm{1}\right]\:{factorise}\:{it} \\ $$
Commented by abdo imad last updated on 03/Jan/18
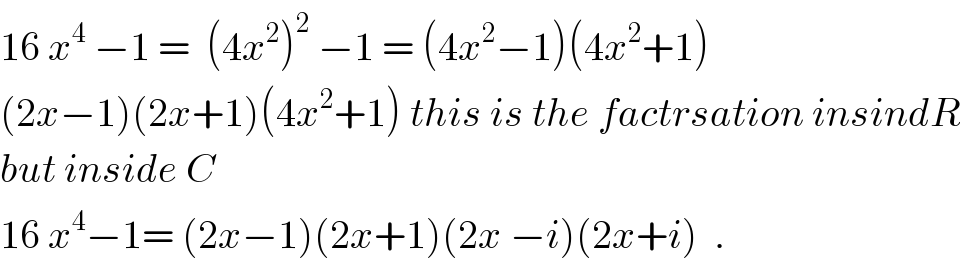
$$\mathrm{16}\:{x}^{\mathrm{4}} \:−\mathrm{1}\:=\:\:\left(\mathrm{4}{x}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{1}\:=\:\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)\:{this}\:{is}\:{the}\:{factrsation}\:{insindR} \\ $$$${but}\:{inside}\:{C} \\ $$$$\mathrm{16}\:{x}^{\mathrm{4}} −\mathrm{1}=\:\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}\:−{i}\right)\left(\mathrm{2}{x}+{i}\right)\:\:. \\ $$
Answered by shiv15031973@gmail.com last updated on 04/Jan/18
![(4x^2 )^2 −(1^2 )^2 =a^2 −b^2 (4x^2 +1)(4x^2 −1) [(4x^2 +1)(2x+1)(2x^× −1)]/(2x^× −1) ∵8x^3 +4x^2 +2x+1](https://www.tinkutara.com/question/Q27279.png)
$$\left(\mathrm{4}{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{1}^{\mathrm{2}} \right)^{\mathrm{2}} ={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)\: \\ $$$$\left[\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}\overset{×} {{x}}−\mathrm{1}\right)\right]/\left(\mathrm{2}\overset{×} {\boldsymbol{{x}}}−\mathrm{1}\right) \\ $$$$\because\mathrm{8}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$
