Question Number 147320 by Gbenga last updated on 19/Jul/21
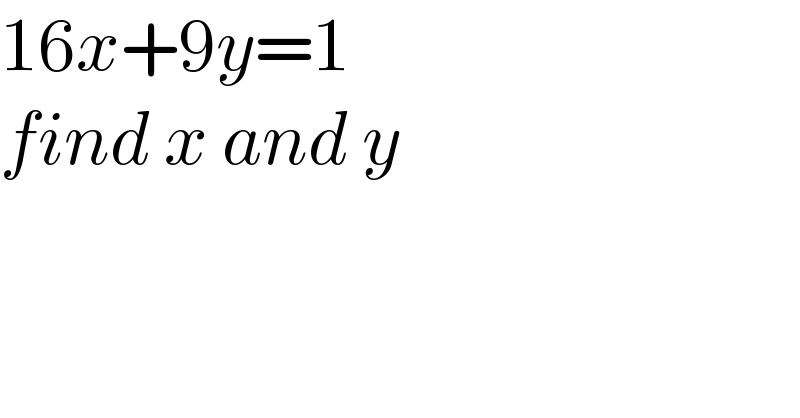
$$\mathrm{16}{x}+\mathrm{9}{y}=\mathrm{1} \\ $$$${find}\:{x}\:{and}\:{y} \\ $$
Answered by floor(10²Eta[1]) last updated on 20/Jul/21
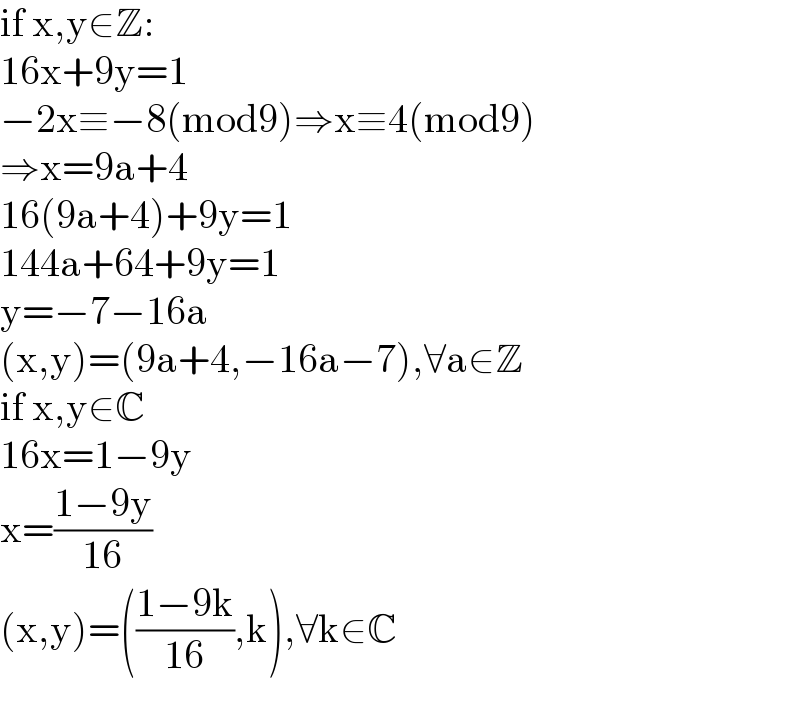
$$\mathrm{if}\:\mathrm{x},\mathrm{y}\in\mathbb{Z}: \\ $$$$\mathrm{16x}+\mathrm{9y}=\mathrm{1} \\ $$$$−\mathrm{2x}\equiv−\mathrm{8}\left(\mathrm{mod9}\right)\Rightarrow\mathrm{x}\equiv\mathrm{4}\left(\mathrm{mod9}\right) \\ $$$$\Rightarrow\mathrm{x}=\mathrm{9a}+\mathrm{4} \\ $$$$\mathrm{16}\left(\mathrm{9a}+\mathrm{4}\right)+\mathrm{9y}=\mathrm{1} \\ $$$$\mathrm{144a}+\mathrm{64}+\mathrm{9y}=\mathrm{1} \\ $$$$\mathrm{y}=−\mathrm{7}−\mathrm{16a} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{9a}+\mathrm{4},−\mathrm{16a}−\mathrm{7}\right),\forall\mathrm{a}\in\mathbb{Z} \\ $$$$\mathrm{if}\:\mathrm{x},\mathrm{y}\in\mathbb{C} \\ $$$$\mathrm{16x}=\mathrm{1}−\mathrm{9y} \\ $$$$\mathrm{x}=\frac{\mathrm{1}−\mathrm{9y}}{\mathrm{16}} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\frac{\mathrm{1}−\mathrm{9k}}{\mathrm{16}},\mathrm{k}\right),\forall\mathrm{k}\in\mathbb{C} \\ $$
Commented by Gbenga last updated on 20/Jul/21

$${thanks}\:{sir} \\ $$
