Question Number 148042 by mathdanisur last updated on 25/Jul/21
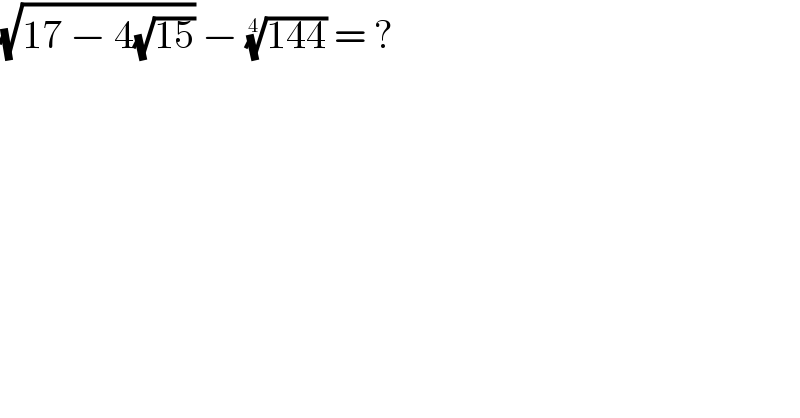
$$\sqrt{\mathrm{17}\:−\:\mathrm{4}\sqrt{\mathrm{15}}}\:−\:\sqrt[{\mathrm{4}}]{\mathrm{144}}\:=\:? \\ $$
Answered by Olaf_Thorendsen last updated on 25/Jul/21
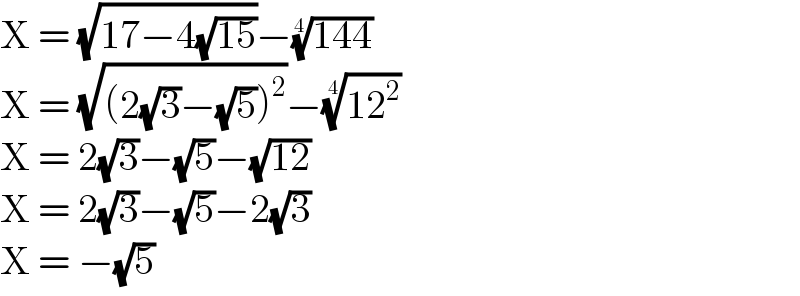
$$\mathrm{X}\:=\:\sqrt{\mathrm{17}−\mathrm{4}\sqrt{\mathrm{15}}}−\sqrt[{\mathrm{4}}]{\mathrm{144}} \\ $$$$\mathrm{X}\:=\:\sqrt{\left(\mathrm{2}\sqrt{\mathrm{3}}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }−\sqrt[{\mathrm{4}}]{\mathrm{12}^{\mathrm{2}} } \\ $$$$\mathrm{X}\:=\:\mathrm{2}\sqrt{\mathrm{3}}−\sqrt{\mathrm{5}}−\sqrt{\mathrm{12}} \\ $$$$\mathrm{X}\:=\:\mathrm{2}\sqrt{\mathrm{3}}−\sqrt{\mathrm{5}}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{X}\:=\:−\sqrt{\mathrm{5}} \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Commented by tabata last updated on 25/Jul/21
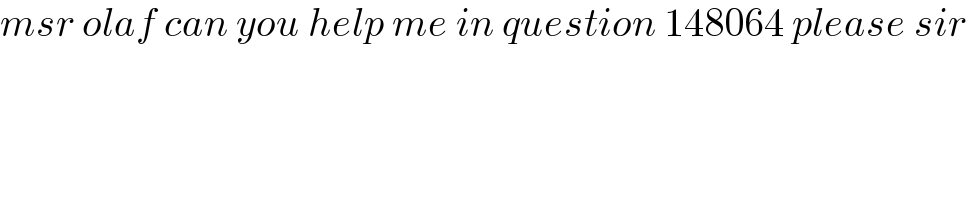
$${msr}\:{olaf}\:{can}\:{you}\:{help}\:{me}\:{in}\:{question}\:\mathrm{148064}\:{please}\:{sir} \\ $$$$ \\ $$
Answered by liberty last updated on 25/Jul/21
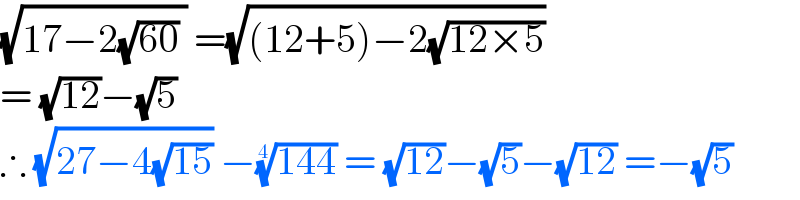
$$\sqrt{\mathrm{17}−\mathrm{2}\sqrt{\mathrm{60}}\:}\:=\sqrt{\left(\mathrm{12}+\mathrm{5}\right)−\mathrm{2}\sqrt{\mathrm{12}×\mathrm{5}}} \\ $$$$=\:\sqrt{\mathrm{12}}−\sqrt{\mathrm{5}} \\ $$$$\therefore\:\sqrt{\mathrm{27}−\mathrm{4}\sqrt{\mathrm{15}}}\:−\sqrt[{\mathrm{4}}]{\mathrm{144}}\:=\:\sqrt{\mathrm{12}}−\sqrt{\mathrm{5}}−\sqrt{\mathrm{12}}\:=−\sqrt{\mathrm{5}} \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thanks}\:{Sir} \\ $$
