Question Number 80917 by jagoll last updated on 08/Feb/20
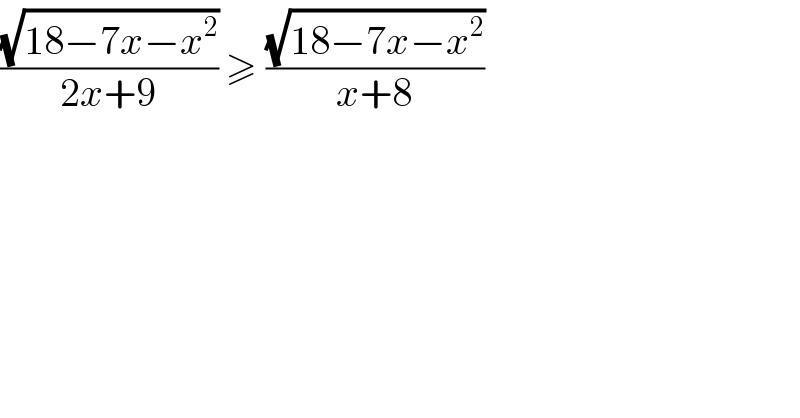
$$\frac{\sqrt{\mathrm{18}−\mathrm{7}{x}−{x}^{\mathrm{2}} }}{\mathrm{2}{x}+\mathrm{9}}\:\geqslant\:\frac{\sqrt{\mathrm{18}−\mathrm{7}{x}−{x}^{\mathrm{2}} }}{{x}+\mathrm{8}} \\ $$
Answered by john santu last updated on 08/Feb/20
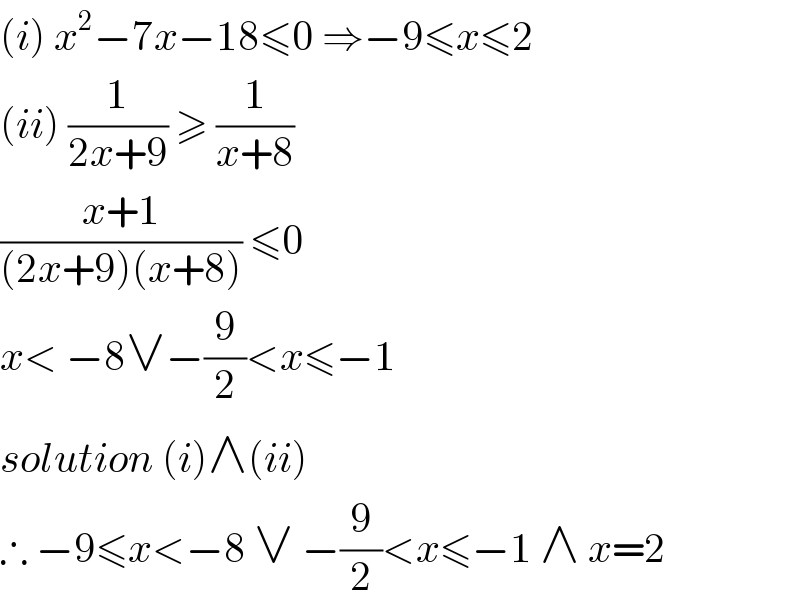
$$\left({i}\right)\:{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{18}\leqslant\mathrm{0}\:\Rightarrow−\mathrm{9}\leqslant{x}\leqslant\mathrm{2} \\ $$$$\left({ii}\right)\:\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{9}}\:\geqslant\:\frac{\mathrm{1}}{{x}+\mathrm{8}} \\ $$$$\frac{{x}+\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{9}\right)\left({x}+\mathrm{8}\right)}\:\leqslant\mathrm{0}\: \\ $$$${x}<\:−\mathrm{8}\vee−\frac{\mathrm{9}}{\mathrm{2}}<{x}\leqslant−\mathrm{1} \\ $$$${solution}\:\left({i}\right)\wedge\left({ii}\right) \\ $$$$\therefore\:−\mathrm{9}\leqslant{x}<−\mathrm{8}\:\vee\:−\frac{\mathrm{9}}{\mathrm{2}}<{x}\leqslant−\mathrm{1}\:\wedge\:{x}=\mathrm{2} \\ $$
Commented by jagoll last updated on 08/Feb/20

$${thx} \\ $$
