Menu Close

18x-2-3y-1-9x-2-18y-2-3z-1-9y-2-18z-2-3x-1-9z-2-

Tinku Tara 0 Comments
Pin




Question Number 93138 by i jagooll last updated on 11/May/20
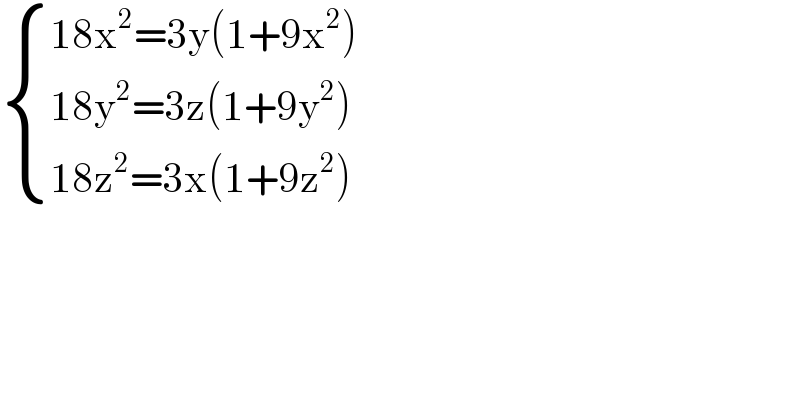
{ ((18x^2 =3y(1+9x^2 ))),((18y^2 =3z(1+9y^2 ))),((18z^2 =3x(1+9z^2 ))) :}
$$\begin{cases}{\mathrm{18x}^{\mathrm{2}} =\mathrm{3y}\left(\mathrm{1}+\mathrm{9x}^{\mathrm{2}} \right)}\\{\mathrm{18y}^{\mathrm{2}} =\mathrm{3z}\left(\mathrm{1}+\mathrm{9y}^{\mathrm{2}} \right)}\\{\mathrm{18z}^{\mathrm{2}} =\mathrm{3x}\left(\mathrm{1}+\mathrm{9z}^{\mathrm{2}} \right)}\end{cases} \\ $$
Answered by john santu last updated on 11/May/20
{ ((x^2 =(y/(6−9y)))),((y^2 = (z/(6−9z)))),((z^2 = (x/(6−9x)))) :} (xyz)^2 = ((xyz)/((6−9x)(6−9y)(6−9z))) (6−9x)(6−9y)(6−9z) = (1/(xyz)) { ((6−9x=(1/x)⇒x=(1/3))),((6−9y=(1/y)⇒y=(1/3))),((6−9z=(1/z)⇒z=(1/3))) :}
$$\begin{cases}{\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{y}}{\mathrm{6}−\mathrm{9y}}}\\{\mathrm{y}^{\mathrm{2}} =\:\frac{\mathrm{z}}{\mathrm{6}−\mathrm{9z}}}\\{\mathrm{z}^{\mathrm{2}} \:=\:\frac{\mathrm{x}}{\mathrm{6}−\mathrm{9x}}}\end{cases} \\ $$$$\left(\mathrm{xyz}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{xyz}}{\left(\mathrm{6}−\mathrm{9x}\right)\left(\mathrm{6}−\mathrm{9y}\right)\left(\mathrm{6}−\mathrm{9z}\right)} \\ $$$$\left(\mathrm{6}−\mathrm{9x}\right)\left(\mathrm{6}−\mathrm{9y}\right)\left(\mathrm{6}−\mathrm{9z}\right)\:=\:\frac{\mathrm{1}}{\mathrm{xyz}} \\ $$$$\begin{cases}{\mathrm{6}−\mathrm{9x}=\frac{\mathrm{1}}{\mathrm{x}}\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{6}−\mathrm{9y}=\frac{\mathrm{1}}{\mathrm{y}}\Rightarrow\mathrm{y}=\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{6}−\mathrm{9z}=\frac{\mathrm{1}}{\mathrm{z}}\Rightarrow\mathrm{z}=\frac{\mathrm{1}}{\mathrm{3}}}\end{cases} \\ $$$$ \\ $$
Answered by MJS last updated on 11/May/20
if x=y=z=c (because of symmetry) ⇒ c=0∨c=(1/3) if x≠y≠z we get x≈−.137591±.0972771i y≈.0812039∓.129974i z≈−.0372460±.147390i and these values are interchangeable
$$\mathrm{if}\:{x}={y}={z}=\mathrm{c}\:\left(\mathrm{because}\:\mathrm{of}\:\mathrm{symmetry}\right)\:\Rightarrow \\ $$$${c}=\mathrm{0}\vee{c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{if}\:{x}\neq{y}\neq{z}\:\mathrm{we}\:\mathrm{get} \\ $$$${x}\approx−.\mathrm{137591}\pm.\mathrm{0972771i} \\ $$$${y}\approx.\mathrm{0812039}\mp.\mathrm{129974i} \\ $$$${z}\approx−.\mathrm{0372460}\pm.\mathrm{147390i} \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{values}\:\mathrm{are}\:\mathrm{interchangeable} \\ $$
Commented by i jagooll last updated on 11/May/20
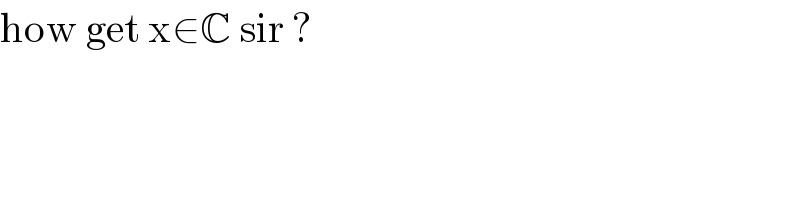
how get x∈C sir ?
$$\mathrm{how}\:\mathrm{get}\:\mathrm{x}\in\mathbb{C}\:\mathrm{sir}\:? \\ $$
Commented by MJS last updated on 11/May/20
18x^2 =3y(9x^2 +1) ⇒ y=((6x^2 )/(9x^2 +1)) 18y^2 =3z(9y^2 +1) ⇒ z=((6y^2 )/(9y^2 +1))=((216x^4 )/(405x^4 +18x^2 +1)) 18z^2 =3x(9z^2 +1) ⇒ 3(3x−2)z^2 +x=0 ⇒ ((583929x(x−(1/3))^2 )/((405x^4 +18x^2 +1)^2 ))(x^6 +((50)/(267))x^5 +((31)/(801))x^4 +(4/(801))x^3 +(7/(7209))x^2 +(2/(21627))x+(1/(64881)))=0 x=0∧x=(1/3) is obvious because of the first attempt solving in R now we must approximate with a good calculator
$$\mathrm{18}{x}^{\mathrm{2}} =\mathrm{3}{y}\left(\mathrm{9}{x}^{\mathrm{2}} +\mathrm{1}\right)\:\Rightarrow\:{y}=\frac{\mathrm{6}{x}^{\mathrm{2}} }{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{18}{y}^{\mathrm{2}} =\mathrm{3}{z}\left(\mathrm{9}{y}^{\mathrm{2}} +\mathrm{1}\right)\:\Rightarrow\:{z}=\frac{\mathrm{6}{y}^{\mathrm{2}} }{\mathrm{9}{y}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{216}{x}^{\mathrm{4}} }{\mathrm{405}{x}^{\mathrm{4}} +\mathrm{18}{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{18}{z}^{\mathrm{2}} =\mathrm{3}{x}\left(\mathrm{9}{z}^{\mathrm{2}} +\mathrm{1}\right)\:\Rightarrow\:\mathrm{3}\left(\mathrm{3}{x}−\mathrm{2}\right){z}^{\mathrm{2}} +{x}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\frac{\mathrm{583929}{x}\left({x}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }{\left(\mathrm{405}{x}^{\mathrm{4}} +\mathrm{18}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\left({x}^{\mathrm{6}} +\frac{\mathrm{50}}{\mathrm{267}}{x}^{\mathrm{5}} +\frac{\mathrm{31}}{\mathrm{801}}{x}^{\mathrm{4}} +\frac{\mathrm{4}}{\mathrm{801}}{x}^{\mathrm{3}} +\frac{\mathrm{7}}{\mathrm{7209}}{x}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{21627}}{x}+\frac{\mathrm{1}}{\mathrm{64881}}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\wedge{x}=\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{is}\:\mathrm{obvious}\:\mathrm{because}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first} \\ $$$$\mathrm{attempt}\:\mathrm{solving}\:\mathrm{in}\:\mathbb{R} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{must}\:\mathrm{approximate}\:\mathrm{with}\:\mathrm{a}\:\mathrm{good} \\ $$$$\mathrm{calculator} \\ $$
Commented by i jagooll last updated on 11/May/20
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *