Menu Close

2-0-4x-x-3-1-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 127521 by mohammad17 last updated on 30/Dec/20
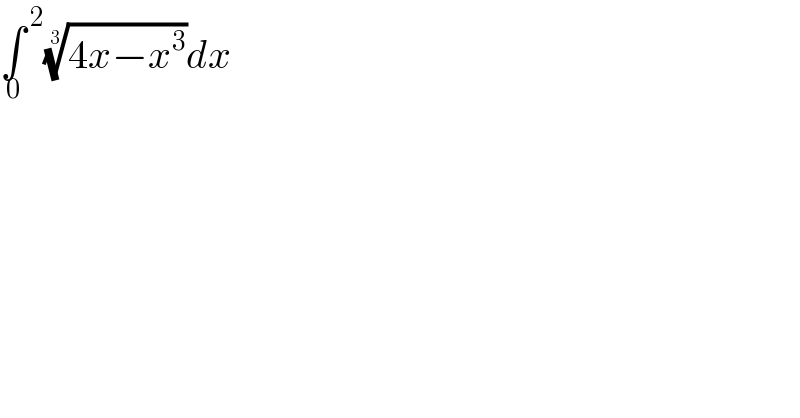
∫^( 2) _0 ((4x−x^3 ))^(1/3) dx
$$\underset{\mathrm{0}} {\int}^{\:\mathrm{2}} \sqrt[{\mathrm{3}}]{\mathrm{4}{x}−{x}^{\mathrm{3}} }{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Dec/20
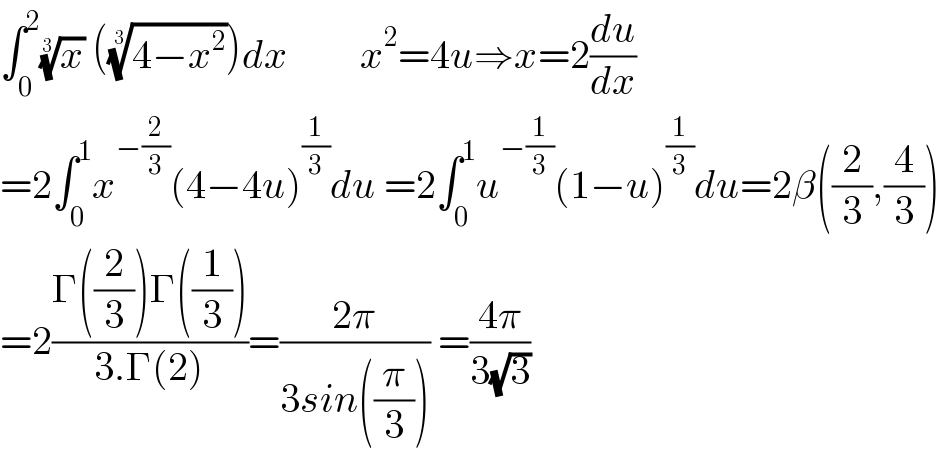
∫_0 ^2 (x)^(1/3) (((4−x^2 ))^(1/3) )dx x^2 =4u⇒x=2(du/dx) =2∫_0 ^1 x^(−(2/3)) (4−4u)^(1/3) du =2∫_0 ^1 u^(−(1/3)) (1−u)^(1/3) du=2β((2/3),(4/3)) =2((Γ((2/3))Γ((1/3)))/(3.Γ(2)))=((2π)/(3sin((π/3)))) =((4π)/(3(√3)))
$$\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt[{\mathrm{3}}]{{x}}\:\left(\sqrt[{\mathrm{3}}]{\mathrm{4}−{x}^{\mathrm{2}} }\right){dx}\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\mathrm{4}{u}\Rightarrow{x}=\mathrm{2}\frac{{du}}{{dx}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{4}−\mathrm{4}{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {du}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {du}=\mathrm{2}\beta\left(\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$=\mathrm{2}\frac{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{3}.\Gamma\left(\mathrm{2}\right)}=\frac{\mathrm{2}\pi}{\mathrm{3}{sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Answered by mathmax by abdo last updated on 01/Jan/21
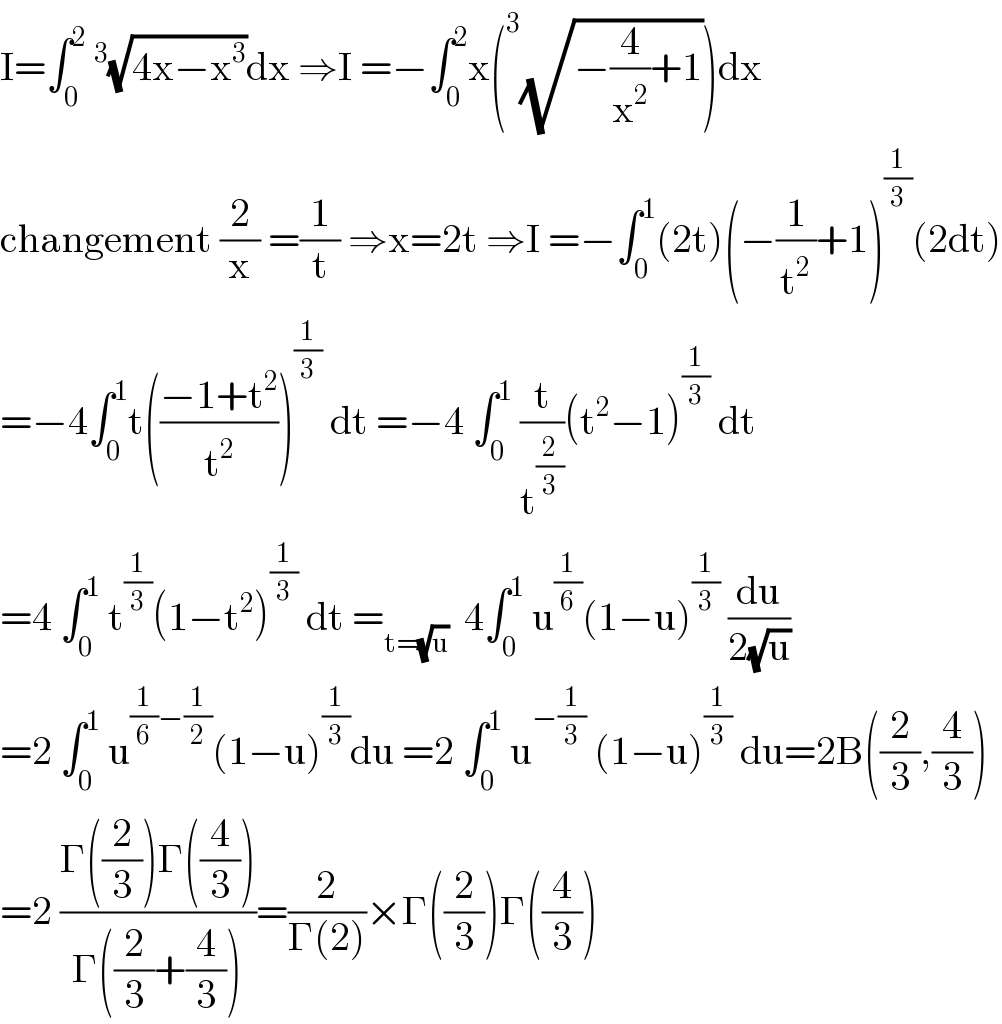
I=∫_0 ^2 ^3 (√(4x−x^3 ))dx ⇒I =−∫_0 ^2 x(^3 (√(−(4/x^2 )+1)))dx changement (2/x) =(1/t) ⇒x=2t ⇒I =−∫_0 ^1 (2t)(−(1/t^2 )+1)^(1/3) (2dt) =−4∫_0 ^1 t(((−1+t^2 )/t^2 ))^(1/3) dt =−4 ∫_0 ^1 (t/t^(2/3) )(t^2 −1)^(1/3) dt =4 ∫_0 ^1 t^(1/3) (1−t^2 )^(1/3) dt =_(t=(√u)) 4∫_0 ^1 u^(1/6) (1−u)^(1/3) (du/(2(√u))) =2 ∫_0 ^1 u^((1/6)−(1/2)) (1−u)^(1/3) du =2 ∫_0 ^1 u^(−(1/3)) (1−u)^(1/3) du=2B((2/3),(4/3)) =2 ((Γ((2/3))Γ((4/3)))/(Γ((2/3)+(4/3))))=(2/(Γ(2)))×Γ((2/3))Γ((4/3))
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{2}} \:^{\mathrm{3}} \sqrt{\mathrm{4x}−\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:\Rightarrow\mathrm{I}\:=−\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{x}\left(^{\mathrm{3}} \sqrt{−\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}}\right)\mathrm{dx} \\ $$$$\mathrm{changement}\:\frac{\mathrm{2}}{\mathrm{x}}\:=\frac{\mathrm{1}}{\mathrm{t}}\:\Rightarrow\mathrm{x}=\mathrm{2t}\:\Rightarrow\mathrm{I}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2t}\right)\left(−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{2dt}\right) \\ $$$$=−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{t}\left(\frac{−\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{dt}\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}}{\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} }\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{dt}\:=_{\mathrm{t}=\sqrt{\mathrm{u}}} \:\:\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{6}}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{u}}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{du}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{3}}} \:\left(\mathrm{1}−\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{du}=\mathrm{2B}\left(\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$=\mathrm{2}\:\frac{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{4}}{\mathrm{3}}\right)}{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{4}}{\mathrm{3}}\right)}=\frac{\mathrm{2}}{\Gamma\left(\mathrm{2}\right)}×\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$
Commented by mathmax by abdo last updated on 01/Jan/21
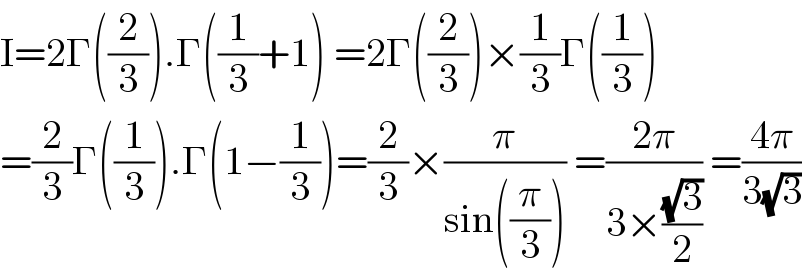
I=2Γ((2/3)).Γ((1/3)+1) =2Γ((2/3))×(1/3)Γ((1/3)) =(2/3)Γ((1/3)).Γ(1−(1/3))=(2/3)×(π/(sin((π/3)))) =((2π)/(3×((√3)/2))) =((4π)/(3(√3)))
$$\mathrm{I}=\mathrm{2}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right)\:=\mathrm{2}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)×\frac{\mathrm{1}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\mathrm{2}\pi}{\mathrm{3}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *