Question Number 61635 by ajfour last updated on 05/Jun/19
![2(∫_0 ^( x) y^3 cos xdx)[((yd^2 y)/dx^2 )−((dy/dx))^2 ] = ky^5 sin x ; y(0)=a, y′(0)=0 . solve the differential equation. (Laplace tranforms might be helpful, i think).](https://www.tinkutara.com/question/Q61635.png)
$$\mathrm{2}\left(\int_{\mathrm{0}} ^{\:{x}} {y}^{\mathrm{3}} \mathrm{cos}\:{xdx}\right)\left[\frac{{yd}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{ky}^{\mathrm{5}} \mathrm{sin}\:{x}\:\:\:\:\:;\:\: \\ $$$$\:\:{y}\left(\mathrm{0}\right)={a},\:{y}'\left(\mathrm{0}\right)=\mathrm{0}\:. \\ $$$$\:{solve}\:{the}\:{differential}\:{equation}. \\ $$$$\left({Laplace}\:{tranforms}\:{might}\right. \\ $$$$\left.\:\:\:\:{be}\:{helpful},\:{i}\:{think}\right). \\ $$
Answered by perlman last updated on 05/Jun/19
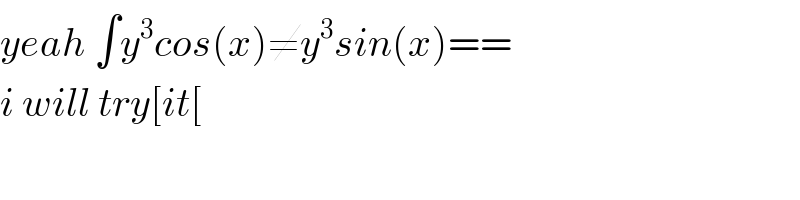
$${yeah}\:\int{y}^{\mathrm{3}} {cos}\left({x}\right)\neq{y}^{\mathrm{3}} {sin}\left({x}\right)== \\ $$$${i}\:{will}\:{try}\left[{it}\left[\right.\right. \\ $$
