2-1-0-2-2018-

Question Number 32877 by 7991 last updated on 05/Apr/18

$$\begin{bmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{bmatrix}^{\mathrm{2018}} =…..??? \\ $$

Answered by Joel578 last updated on 05/Apr/18

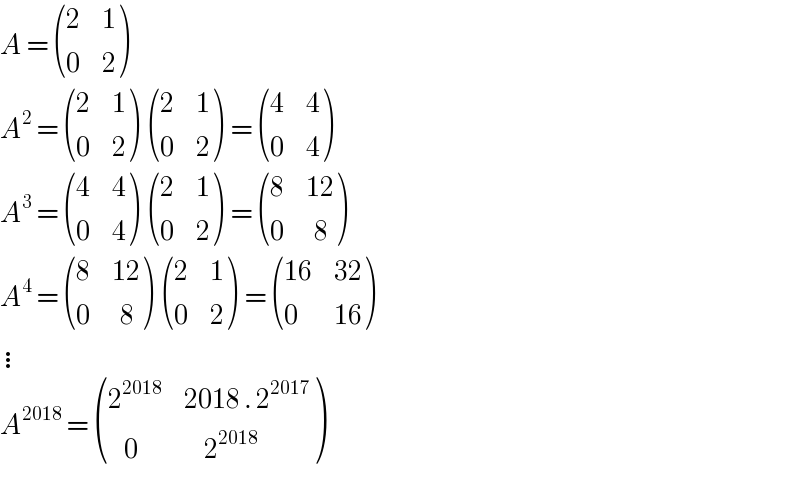
$${A}\:=\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix} \\ $$$${A}^{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{4}}&{\mathrm{4}}\\{\mathrm{0}}&{\mathrm{4}}\end{pmatrix} \\ $$$${A}^{\mathrm{3}} \:=\:\begin{pmatrix}{\mathrm{4}}&{\mathrm{4}}\\{\mathrm{0}}&{\mathrm{4}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{8}}&{\mathrm{12}}\\{\mathrm{0}}&{\:\:\mathrm{8}}\end{pmatrix} \\ $$$${A}^{\mathrm{4}} \:=\:\begin{pmatrix}{\mathrm{8}}&{\mathrm{12}}\\{\mathrm{0}}&{\:\:\mathrm{8}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{16}}&{\mathrm{32}}\\{\mathrm{0}}&{\mathrm{16}}\end{pmatrix} \\ $$$$\vdots \\ $$$${A}^{\mathrm{2018}} \:=\:\begin{pmatrix}{\mathrm{2}^{\mathrm{2018}} }&{\mathrm{2018}\:.\:\mathrm{2}^{\mathrm{2017}} }\\{\:\:\:\:\mathrm{0}}&{\:\:\:\:\:\mathrm{2}^{\mathrm{2018}} }\end{pmatrix} \\ $$

Commented by MJS last updated on 05/Apr/18

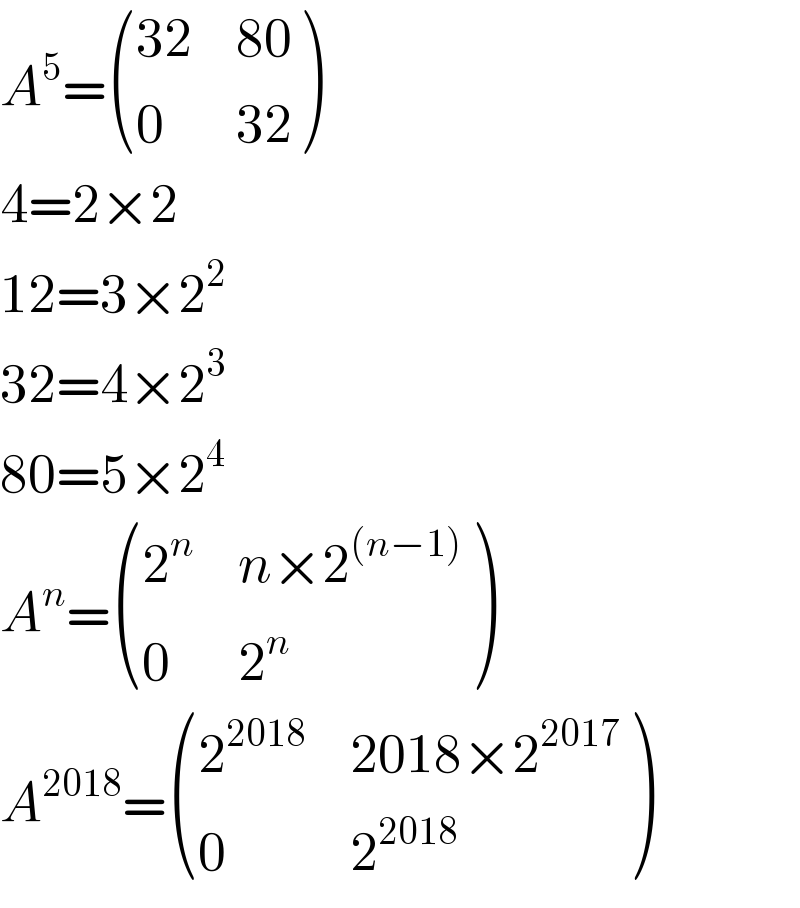
$${A}^{\mathrm{5}} =\begin{pmatrix}{\mathrm{32}}&{\mathrm{80}}\\{\mathrm{0}}&{\mathrm{32}}\end{pmatrix} \\ $$$$\mathrm{4}=\mathrm{2}×\mathrm{2} \\ $$$$\mathrm{12}=\mathrm{3}×\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{32}=\mathrm{4}×\mathrm{2}^{\mathrm{3}} \\ $$$$\mathrm{80}=\mathrm{5}×\mathrm{2}^{\mathrm{4}} \\ $$$${A}^{{n}} =\begin{pmatrix}{\mathrm{2}^{{n}} }&{{n}×\mathrm{2}^{\left({n}−\mathrm{1}\right)} }\\{\mathrm{0}}&{\mathrm{2}^{{n}} }\end{pmatrix} \\ $$$${A}^{\mathrm{2018}} =\begin{pmatrix}{\mathrm{2}^{\mathrm{2018}} }&{\mathrm{2018}×\mathrm{2}^{\mathrm{2017}} }\\{\mathrm{0}}&{\mathrm{2}^{\mathrm{2018}} }\end{pmatrix} \\ $$

Commented by Joel578 last updated on 05/Apr/18

$${thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com