Question Number 101601 by Dwaipayan Shikari last updated on 03/Jul/20
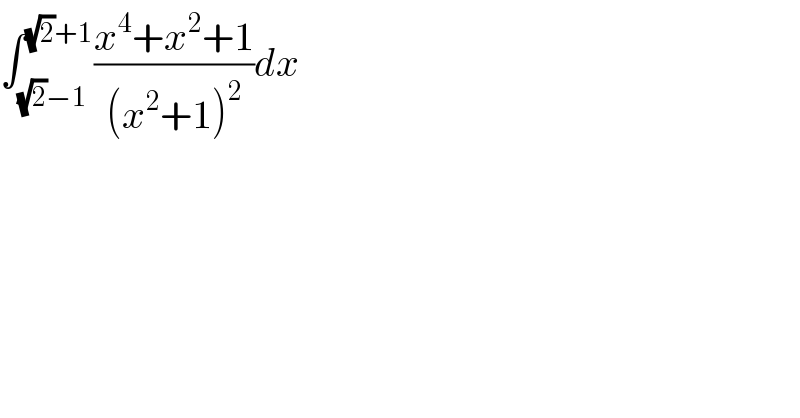
$$\int_{\sqrt{\mathrm{2}}−\mathrm{1}} ^{\sqrt{\mathrm{2}}+\mathrm{1}} \frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by bemath last updated on 03/Jul/20
![∫ (((x^2 +1)^2 −x^2 )/((x^2 +1)^2 )) dx = x−∫ (x^2 /((x^2 +1)^2 )) dx I_2 = ∫ (x^2 /((x^2 +1)^2 )) dx [ x = tan p ] I_2 = ∫ ((tan^2 p . sec^2 p dp)/(sec^4 p)) = ∫ tan^2 p cos^2 p dp = ∫ ((1/2)−(1/2)cos 2p) dp = (1/2)p −(1/4)sin 2p =(1/2)tan^(−1) (x)−(x/(2(x^2 +1))) I= 2−(1/2)(tan^(−1) ((√2)+1)−tan^(−1) ((√2)−1)) −(1/2)((((√2)+1)/(4+2(√2))) −(((√2)−1)/(4−2(√2))))](https://www.tinkutara.com/question/Q101602.png)
$$\int\:\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx}\:=\:\mathrm{x}−\int\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{2}} =\:\int\:\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\: \\ $$$$\left[\:{x}\:=\:\mathrm{tan}\:{p}\:\right]\: \\ $$$$\mathrm{I}_{\mathrm{2}} \:=\:\int\:\frac{\mathrm{tan}\:^{\mathrm{2}} {p}\:.\:\mathrm{sec}\:^{\mathrm{2}} {p}\:{dp}}{\mathrm{sec}\:^{\mathrm{4}} {p}} \\ $$$$=\:\int\:\mathrm{tan}\:^{\mathrm{2}} {p}\:\mathrm{cos}\:^{\mathrm{2}} {p}\:{dp}\: \\ $$$$=\:\int\:\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{p}\right)\:{dp} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{p}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{p}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\frac{{x}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${I}=\:\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}\:−\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}\right) \\ $$
