Question Number 119679 by Khalmohmmad last updated on 26/Oct/20
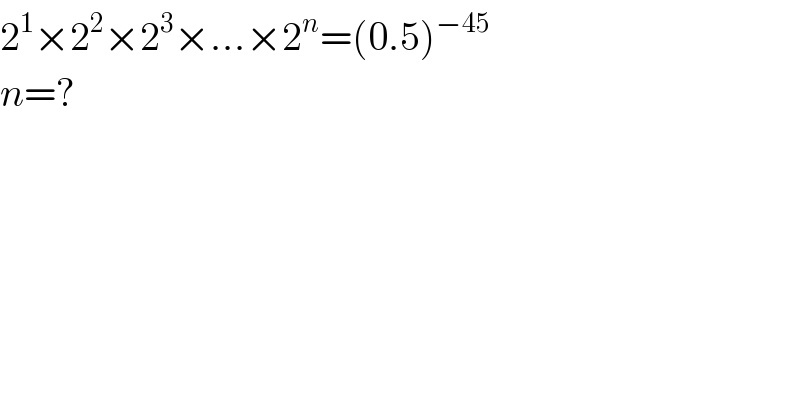
$$\mathrm{2}^{\mathrm{1}} ×\mathrm{2}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{3}} ×…×\mathrm{2}^{{n}} =\left(\mathrm{0}.\mathrm{5}\right)^{−\mathrm{45}} \\ $$$${n}=? \\ $$
Answered by Ar Brandon last updated on 26/Oct/20
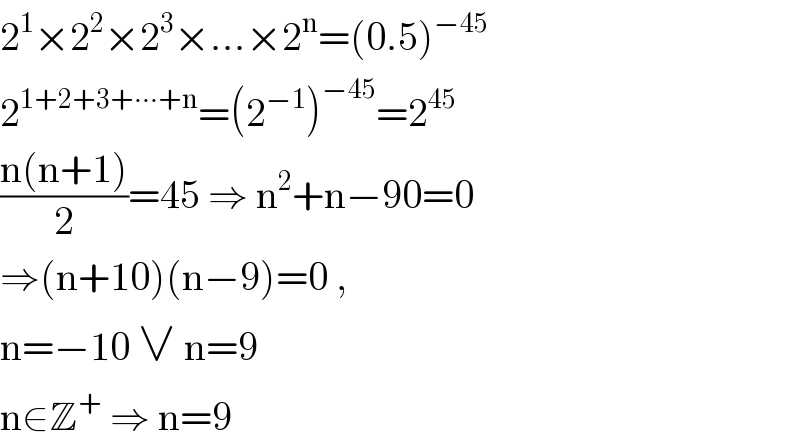
$$\mathrm{2}^{\mathrm{1}} ×\mathrm{2}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{3}} ×…×\mathrm{2}^{\mathrm{n}} =\left(\mathrm{0}.\mathrm{5}\right)^{−\mathrm{45}} \\ $$$$\mathrm{2}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+\centerdot\centerdot\centerdot+\mathrm{n}} =\left(\mathrm{2}^{−\mathrm{1}} \right)^{−\mathrm{45}} =\mathrm{2}^{\mathrm{45}} \\ $$$$\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{45}\:\Rightarrow\:\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{90}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{n}+\mathrm{10}\right)\left(\mathrm{n}−\mathrm{9}\right)=\mathrm{0}\:,\: \\ $$$$\mathrm{n}=−\mathrm{10}\:\vee\:\mathrm{n}=\mathrm{9}\: \\ $$$$\mathrm{n}\in\mathbb{Z}^{+} \:\Rightarrow\:\mathrm{n}=\mathrm{9} \\ $$
