Question Number 60577 by naka3546 last updated on 22/May/19

$$\mathrm{2}\sqrt{\mathrm{1}\:+\:\mathrm{3}\sqrt{\mathrm{1}\:+\:\mathrm{5}\sqrt{\mathrm{1}\:+\:\mathrm{7}\sqrt{\mathrm{1}\:+\:\mathrm{11}\sqrt{\mathrm{1}\:+\:\mathrm{13}\sqrt{\mathrm{1}\:+\:\mathrm{17}\sqrt{…}}}}}}}\:\:=\:\:{x} \\ $$$${x}\:\:=\:\:? \\ $$
Commented by ajfour last updated on 22/May/19
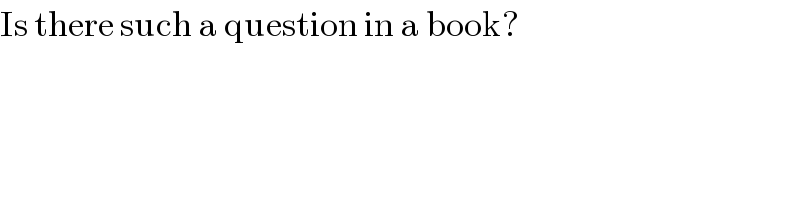
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{such}\:\mathrm{a}\:\mathrm{question}\:\mathrm{in}\:\mathrm{a}\:\mathrm{book}? \\ $$
Answered by Prithwish sen last updated on 22/May/19

$$\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{3}\right)=\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\left(\mathrm{n}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$=\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{1}+\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{4}\right)} \\ $$$$=\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{1}+\left(\mathrm{n}+\mathrm{2}\right)\sqrt{\left(\mathrm{n}+\mathrm{4}\right)^{\mathrm{2}} }} \\ $$$$=\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{1}+\left(\mathrm{n}+\mathrm{2}\right)\sqrt{\mathrm{1}+\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{5}\right)}} \\ $$$$=\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{1}+\left(\mathrm{n}+\mathrm{2}\right)\sqrt{\mathrm{1}+\left(\mathrm{n}+\mathrm{3}\right)\sqrt{\left(\mathrm{n}+\mathrm{5}\right)^{\mathrm{2}} }}} \\ $$$$\mathrm{and}\:\mathrm{so}\:\mathrm{on} \\ $$$$\mathrm{putting}\:\mathrm{n}=\mathrm{l} \\ $$$$\mathrm{8}=\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+\mathrm{5}\sqrt{\mathrm{1}+…….}}}} \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{qiestion}\:\mathrm{ok}? \\ $$
Commented by ajfour last updated on 22/May/19

$$\mathrm{yes}\:\mathrm{Sir},\:\mathrm{very}\:\mathrm{fine}\:\mathrm{one}\:\mathrm{this}\:\mathrm{is}. \\ $$
Commented by Prithwish sen last updated on 22/May/19

$$\mathrm{thank}\:\mathrm{you}. \\ $$
