2-1-x-2-1-x-2-dx-

Question Number 36892 by anik last updated on 06/Jun/18

$$\mathrm{2}.\:\int\left[\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)/\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\right]{dx}=? \\ $$

Commented by math khazana by abdo last updated on 11/Jun/18

let I = ∫ (√(((1−x^2 )/(1+x^2 )) )) dx changement x=sint give I = ∫ ((cost)/( (√(2cos^2 t −1)))) costdt = ∫ ((cos^2 t)/( (√(2 cos^2 t −1)))) dt = ∫ (1/((1+tan^2 t)(√(2(1/(1+tan^2 t))−1))))dt = ∫ (dt/((1+tan^2 t)(√(2−1−tan^2 t))))(√(1+tan^2 t)) dt = ∫ (dt/( (√(1+tan^2 t))(√(1−tan^2 t)))) changement tant =u give I = ∫ (1/( (√(1+u^2 ))(√(1−u^2 )))) (du/(1+u^2 )) = ∫ (du/((1+u^2 )(√(1−u^4 )))) ....be continued....

$${let}\:{I}\:\:=\:\int\:\:\sqrt{\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:}\:{dx}\:{changement}\:{x}={sint}\:{give} \\ $$$${I}\:\:=\:\:\int\:\:\:\frac{{cost}}{\:\sqrt{\mathrm{2}{cos}^{\mathrm{2}} {t}\:−\mathrm{1}}}\:{costdt} \\ $$$$=\:\int\:\:\:\:\:\frac{{cos}^{\mathrm{2}} {t}}{\:\sqrt{\mathrm{2}\:{cos}^{\mathrm{2}} {t}\:−\mathrm{1}}}\:{dt}\:=\:\int\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)\sqrt{\mathrm{2}\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {t}}−\mathrm{1}}}{dt} \\ $$$$=\:\int\:\:\:\:\:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)\sqrt{\mathrm{2}−\mathrm{1}−{tan}^{\mathrm{2}} {t}}}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}\:{dt} \\ $$$$=\:\int\:\:\:\:\:\:\:\frac{{dt}}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}\sqrt{\mathrm{1}−{tan}^{\mathrm{2}} {t}}}\:\:{changement} \\ $$$${tant}\:={u}\:\:{give} \\ $$$${I}\:=\:\:\int\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\:\:\frac{{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{u}^{\mathrm{4}} }}\:\:….{be}\:{continued}…. \\ $$$$ \\ $$

Answered by anik last updated on 06/Jun/18

Commented by anik last updated on 06/Jun/18

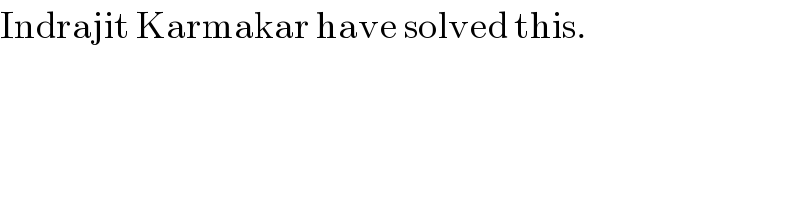
$$\mathrm{Indrajit}\:\mathrm{Karmakar}\:\mathrm{have}\:\mathrm{solved}\:\mathrm{this}. \\ $$

Commented by MJS last updated on 06/Jun/18

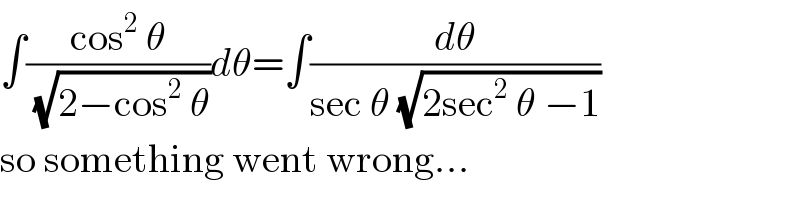
∫((cos^2 θ)/( (√(2−cos^2 θ))))dθ=∫(dθ/(sec θ (√(2sec^2 θ −1)))) so something went wrong...

$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\:\sqrt{\mathrm{2}−\mathrm{cos}^{\mathrm{2}} \:\theta}}{d}\theta=\int\frac{{d}\theta}{\mathrm{sec}\:\theta\:\sqrt{\mathrm{2sec}^{\mathrm{2}} \:\theta\:−\mathrm{1}}} \\ $$$$\mathrm{so}\:\mathrm{something}\:\mathrm{went}\:\mathrm{wrong}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply