2-15-11-40-26-75-47-120-

Question Number 180207 by Acem last updated on 09/Nov/22

$$\:\frac{\mathrm{2}}{\mathrm{15}}\:,\:\:\frac{\mathrm{11}}{\mathrm{40}}\:\:,\:\:\frac{\mathrm{26}}{\mathrm{75}}\:\:,\:\:\frac{\mathrm{47}}{\mathrm{120}}\:\:,\:… \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 09/Nov/22

Numerators: [(2, ,(11), ,(26), ,(47), ,(74)),( ,9, ,(15), ,(21), ,(27), ),( , ,( 6), ,6, ,6, , ) ] Denominators: [((15), ,(40), ,(75), ,(120), ,(175)),( ,(25), ,(35), ,(45), ,(55), ),( , ,( 10), ,(10), ,(10), , ) ] Next term:((74)/(175))

$${Numerators}: \\ $$$$\begin{bmatrix}{\mathrm{2}}&{\:}&{\mathrm{11}}&{\:}&{\mathrm{26}}&{\:}&{\mathrm{47}}&{\:}&{\mathrm{74}}\\{\:}&{\mathrm{9}}&{\:}&{\mathrm{15}}&{\:}&{\mathrm{21}}&{\:}&{\mathrm{27}}&{\:}\\{\:}&{\:}&{\:\mathrm{6}}&{\:}&{\mathrm{6}}&{\:}&{\mathrm{6}}&{\:}&{\:}\end{bmatrix}\:\: \\ $$$${Denominators}: \\ $$$$\begin{bmatrix}{\mathrm{15}}&{\:}&{\mathrm{40}}&{\:}&{\mathrm{75}}&{\:}&{\mathrm{120}}&{\:}&{\mathrm{175}}\\{\:}&{\mathrm{25}}&{\:}&{\mathrm{35}}&{\:}&{\mathrm{45}}&{\:}&{\mathrm{55}}&{\:}\\{\:}&{\:}&{\:\mathrm{10}}&{\:}&{\mathrm{10}}&{\:}&{\mathrm{10}}&{\:}&{\:}\end{bmatrix}\: \\ $$$${Next}\:{term}:\frac{\mathrm{74}}{\mathrm{175}}\:\: \\ $$

Commented by Acem last updated on 09/Nov/22

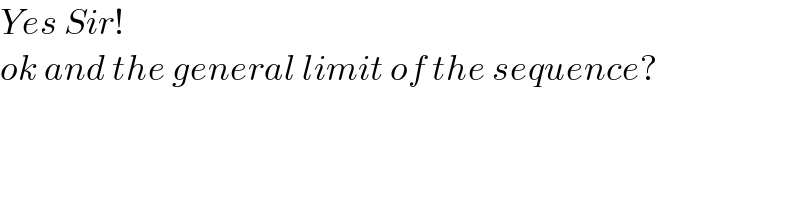
$${Yes}\:{Sir}!\: \\ $$$${ok}\:{and}\:{the}\:{general}\:{limit}\:{of}\:{the}\:{sequence}? \\ $$

Commented by Frix last updated on 09/Nov/22

$$\frac{\mathrm{6}}{\mathrm{10}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$

Answered by Frix last updated on 09/Nov/22

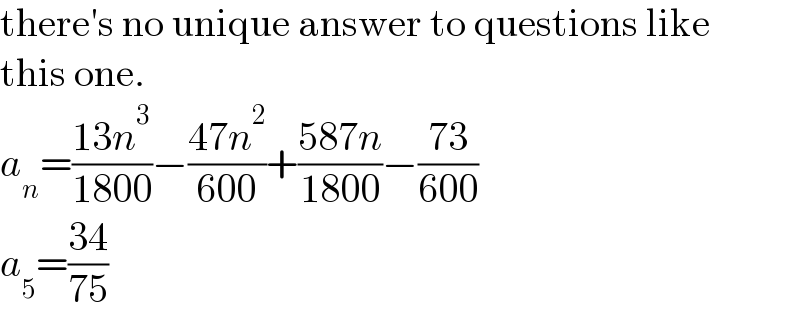
there′s no unique answer to questions like this one. a_n =((13n^3 )/(1800))−((47n^2 )/(600))+((587n)/(1800))−((73)/(600)) a_5 =((34)/(75))

$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{unique}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{questions}\:\mathrm{like} \\ $$$$\mathrm{this}\:\mathrm{one}. \\ $$$${a}_{{n}} =\frac{\mathrm{13}{n}^{\mathrm{3}} }{\mathrm{1800}}−\frac{\mathrm{47}{n}^{\mathrm{2}} }{\mathrm{600}}+\frac{\mathrm{587}{n}}{\mathrm{1800}}−\frac{\mathrm{73}}{\mathrm{600}} \\ $$$${a}_{\mathrm{5}} =\frac{\mathrm{34}}{\mathrm{75}} \\ $$

Commented by Rasheed.Sindhi last updated on 09/Nov/22

$${Right}\:{sir}!\: \\ $$

Answered by Ar Brandon last updated on 09/Nov/22

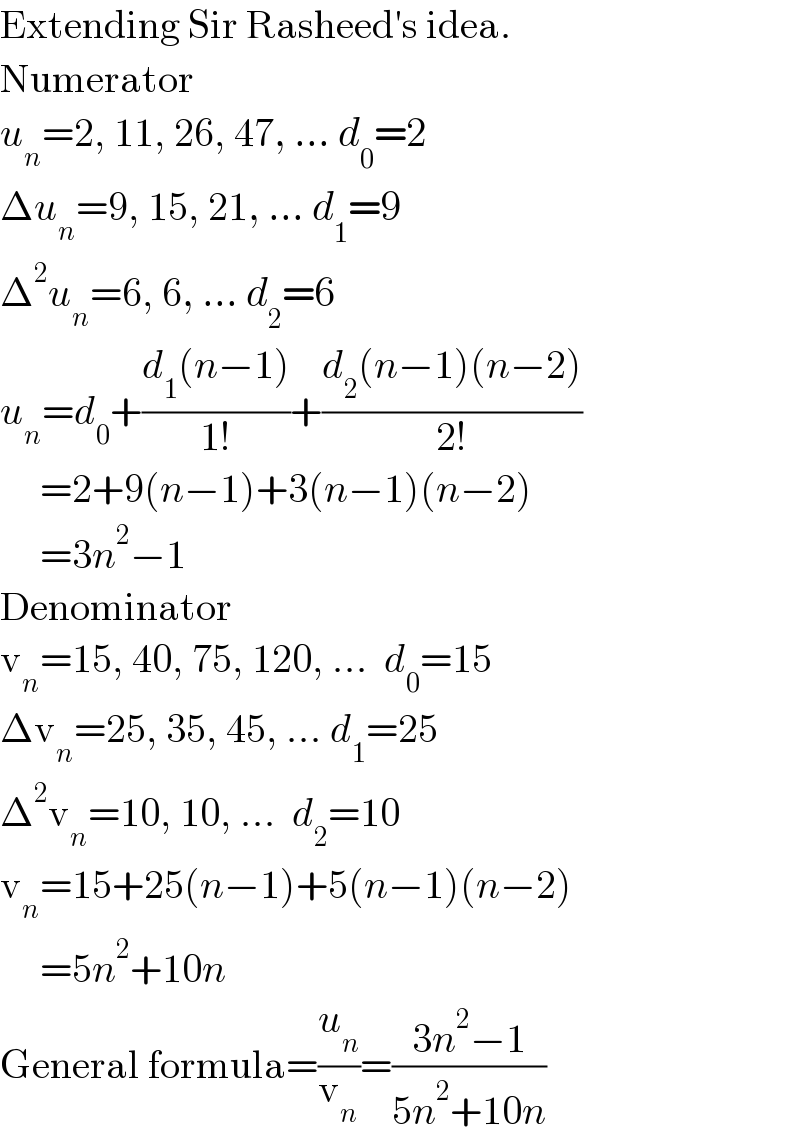
Extending Sir Rasheed′s idea. Numerator u_n =2, 11, 26, 47, ... d_0 =2 Δu_n =9, 15, 21, ... d_1 =9 Δ^2 u_n =6, 6, ... d_2 =6 u_n =d_0 +((d_1 (n−1))/(1!))+((d_2 (n−1)(n−2))/(2!)) =2+9(n−1)+3(n−1)(n−2) =3n^2 −1 Denominator v_n =15, 40, 75, 120, ... d_0 =15 Δv_n =25, 35, 45, ... d_1 =25 Δ^2 v_n =10, 10, ... d_2 =10 v_n =15+25(n−1)+5(n−1)(n−2) =5n^2 +10n General formula=(u_n /v_n )=((3n^2 −1)/(5n^2 +10n))

$$\mathrm{Extending}\:\mathrm{Sir}\:\mathrm{Rasheed}'\mathrm{s}\:\mathrm{idea}. \\ $$$$\mathrm{Numerator}\: \\ $$$${u}_{{n}} =\mathrm{2},\:\mathrm{11},\:\mathrm{26},\:\mathrm{47},\:…\:{d}_{\mathrm{0}} =\mathrm{2} \\ $$$$\Delta{u}_{{n}} =\mathrm{9},\:\mathrm{15},\:\mathrm{21},\:…\:{d}_{\mathrm{1}} =\mathrm{9} \\ $$$$\Delta^{\mathrm{2}} {u}_{{n}} =\mathrm{6},\:\mathrm{6},\:…\:{d}_{\mathrm{2}} =\mathrm{6} \\ $$$${u}_{{n}} ={d}_{\mathrm{0}} +\frac{{d}_{\mathrm{1}} \left({n}−\mathrm{1}\right)}{\mathrm{1}!}+\frac{{d}_{\mathrm{2}} \left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{2}!} \\ $$$$\:\:\:\:\:=\mathrm{2}+\mathrm{9}\left({n}−\mathrm{1}\right)+\mathrm{3}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:=\mathrm{3}{n}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{Denominator} \\ $$$$\mathrm{v}_{{n}} =\mathrm{15},\:\mathrm{40},\:\mathrm{75},\:\mathrm{120},\:…\:\:{d}_{\mathrm{0}} =\mathrm{15} \\ $$$$\Delta\mathrm{v}_{{n}} =\mathrm{25},\:\mathrm{35},\:\mathrm{45},\:…\:{d}_{\mathrm{1}} =\mathrm{25} \\ $$$$\Delta^{\mathrm{2}} \mathrm{v}_{{n}} =\mathrm{10},\:\mathrm{10},\:…\:\:{d}_{\mathrm{2}} =\mathrm{10} \\ $$$$\mathrm{v}_{{n}} =\mathrm{15}+\mathrm{25}\left({n}−\mathrm{1}\right)+\mathrm{5}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:=\mathrm{5}{n}^{\mathrm{2}} +\mathrm{10}{n} \\ $$$$\mathrm{General}\:\mathrm{formula}=\frac{{u}_{{n}} }{\mathrm{v}_{{n}} }=\frac{\mathrm{3}{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{5}{n}^{\mathrm{2}} +\mathrm{10}{n}} \\ $$

Commented by Acem last updated on 09/Nov/22

$${Very}\:{well}\:{Sir}!\:{Thanksss} \\ $$

Answered by Acem last updated on 09/Nov/22

Commented by Acem last updated on 09/Nov/22

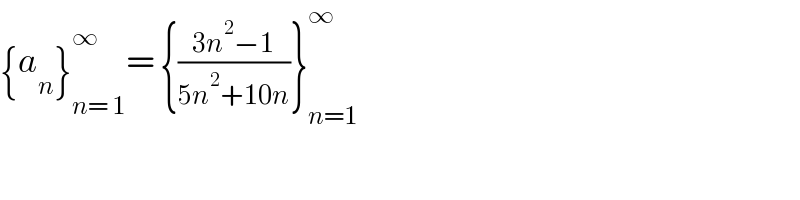
{a_n }_(n= 1) ^∞ = {((3n^2 −1)/(5n^2 +10n))}_(n=1) ^∞

$$\left\{{a}_{{n}} \right\}_{{n}=\:\mathrm{1}} ^{\infty} =\:\left\{\frac{\mathrm{3}{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{5}{n}^{\mathrm{2}} +\mathrm{10}{n}}\right\}_{{n}=\mathrm{1}} ^{\infty} \\ $$$$ \\ $$

Answered by MJS_new last updated on 09/Nov/22

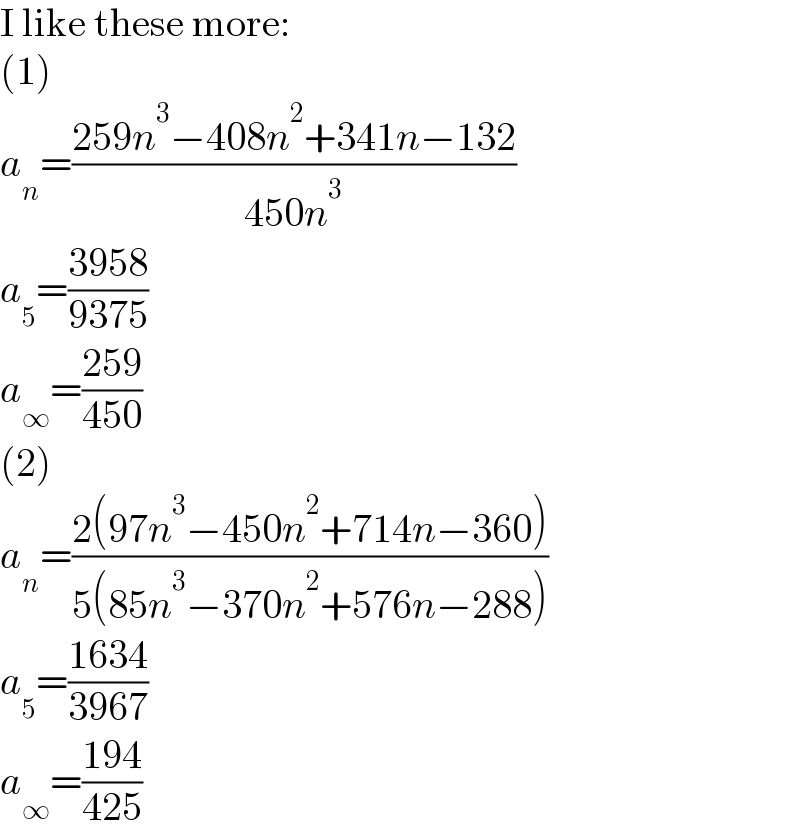
I like these more: (1) a_n =((259n^3 −408n^2 +341n−132)/(450n^3 )) a_5 =((3958)/(9375)) a_∞ =((259)/(450)) (2) a_n =((2(97n^3 −450n^2 +714n−360))/(5(85n^3 −370n^2 +576n−288))) a_5 =((1634)/(3967)) a_∞ =((194)/(425))

$$\mathrm{I}\:\mathrm{like}\:\mathrm{these}\:\mathrm{more}: \\ $$$$\left(\mathrm{1}\right) \\ $$$${a}_{{n}} =\frac{\mathrm{259}{n}^{\mathrm{3}} −\mathrm{408}{n}^{\mathrm{2}} +\mathrm{341}{n}−\mathrm{132}}{\mathrm{450}{n}^{\mathrm{3}} } \\ $$$${a}_{\mathrm{5}} =\frac{\mathrm{3958}}{\mathrm{9375}} \\ $$$${a}_{\infty} =\frac{\mathrm{259}}{\mathrm{450}} \\ $$$$\left(\mathrm{2}\right) \\ $$$${a}_{{n}} =\frac{\mathrm{2}\left(\mathrm{97}{n}^{\mathrm{3}} −\mathrm{450}{n}^{\mathrm{2}} +\mathrm{714}{n}−\mathrm{360}\right)}{\mathrm{5}\left(\mathrm{85}{n}^{\mathrm{3}} −\mathrm{370}{n}^{\mathrm{2}} +\mathrm{576}{n}−\mathrm{288}\right)} \\ $$$${a}_{\mathrm{5}} =\frac{\mathrm{1634}}{\mathrm{3967}} \\ $$$${a}_{\infty} =\frac{\mathrm{194}}{\mathrm{425}} \\ $$

Facebook Tweet Pin

2-15-11-40-26-75-47-120-

Leave a Reply Cancel reply