Question Number 102652 by Dwaipayan Shikari last updated on 10/Jul/20

$$\mathrm{2}+\mathrm{18}+\mathrm{156}+\mathrm{1388}+…{n}\:{terms} \\ $$
Commented by Dwaipayan Shikari last updated on 10/Jul/20
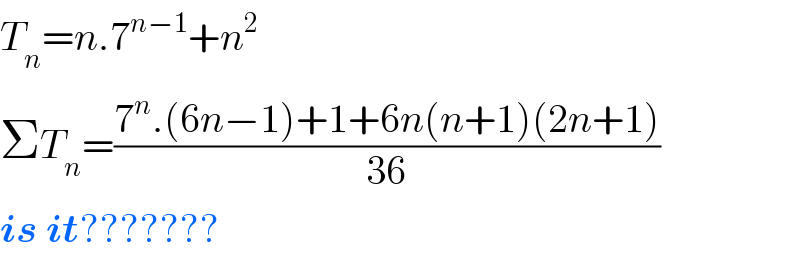
$${T}_{{n}} ={n}.\mathrm{7}^{{n}−\mathrm{1}} +{n}^{\mathrm{2}} \\ $$$$\Sigma{T}_{{n}} =\frac{\mathrm{7}^{{n}} .\left(\mathrm{6}{n}−\mathrm{1}\right)+\mathrm{1}+\mathrm{6}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{36}} \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{it}}??????? \\ $$
Commented by prakash jain last updated on 10/Jul/20

$$\mathrm{You}\:\mathrm{cannot}\:\mathrm{really}\:\mathrm{deduce}\:\mathrm{any} \\ $$$$\mathrm{expression}\:\mathrm{given}\:\mathrm{only}\:\mathrm{a}\:\mathrm{finite} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{term}. \\ $$$$\mathrm{Suppose}\:\mathrm{only}\:\mathrm{4}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{given} \\ $$$${f}\left({n}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {n}+{a}_{\mathrm{2}} {n}^{\mathrm{2}} +{a}_{\mathrm{3}} {n}^{\mathrm{3}} \\ $$$$\mathrm{and}\:\mathrm{solving}\:\mathrm{for}\:\mathrm{given}\:\mathrm{value}\:\mathrm{will} \\ $$$$\mathrm{give}\:\mathrm{you}\:\mathrm{one}\:\mathrm{solution}. \\ $$$$\mathrm{If}\:{f}\left({n}\right)\:\mathrm{satifies}\:\mathrm{first}\:\mathrm{4}\:\mathrm{terms}\:\mathrm{then} \\ $$$${g}\left({n}\right)={f}\left({n}\right)+\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)\left({n}−\mathrm{4}\right){h}\left({n}\right) \\ $$$${will}\:{also}\:{satisfy}\:{the}\:{given} \\ $$$${condition}.\:{where}\:{h}\left({n}\right)\:{is}\:{any} \\ $$$${arbitrary}\:{function}\:{of}\:{n}. \\ $$$${T}_{{n}} ={n}\mathrm{7}^{{n}−\mathrm{1}} +{n}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)\left({n}−\mathrm{4}\right){h}\left({n}\right) \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{valid}.\:\mathrm{where}\:{h}\left({n}\right)\:\mathrm{could} \\ $$$$\mathrm{be}\:\mathrm{anything}. \\ $$
